Worked examples on series-parallel circuits

WORKED EXAMPLES ON SERIES-PARALLEL CIRCUITS

 

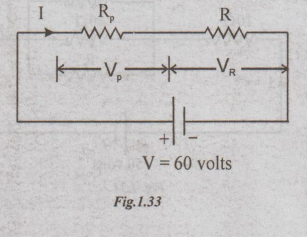
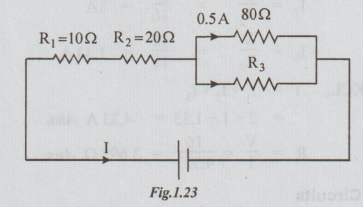
Example 1 Find the voltage across R₁ and R₂

Also find the value of R₃

Solution: For understanding easily the given circuit can be re-drawn as shown below:

By Ohm's law, Voltage across 80Ω = 40 volts

 As 80 Ω and R₃ are in parallel, V_R3 = 40 volts

i.e., Voltage across R₃ = 40 volts

Let the equivalent of parallel combination of 80 and R₃ be R_p.

Hence the circuit becomes as

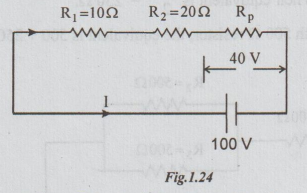
voltage across (R₁ + R₂) = 100 - 40 = 60 volts

i.e., I[R₁ + R₂] = 60 volts

I = 60/ R₁+R₂ = 60/10+20 = 2A

By ohm's law V_RI = IR₁=2 ×10=20 volts

V_R2 = IR₂ = 2 × 20 = 40 volts

By KCL, I = 0.5+I_R3

⇒ I_R3 = I-0.5 = 2-0.5 = 1.5A

R₃ = V_R3/I_R3  = 40/1.5 = 26.7Ω

Ans: (i) V_R1 = 20volts

(ii) V_R2= 40volts

(iii) R₃ = 26.7 Ω

 

Example 2 Find V in the circuit in fig. 1.25

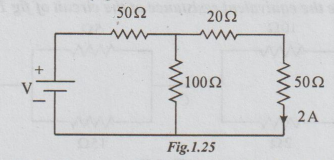
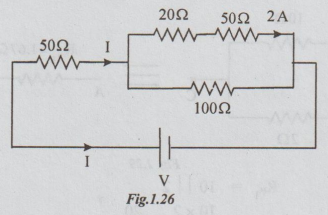
Solution: Re-drawing the circuit given, we obtain the following fig. 1.25

Given that, I₂₀ = I₅₀ = 2A

 By ohm's law, V₂₀ = I₂₀ × 20 = 2× 20 = 40 volts

And V₅₀= I₅₀ × 20 = 2 × 50 =100 volts

V₂₀ + V ₅₀ = 40 + 100 = 140 volts

⇒ V₇₀ = 140 volts

As 100 Ω and (20+ 50) are in parallel.

V₁₀₀ = V₇₀ = 140

⇒ By ohm's law, I₁₀₀ = 140/100 = 1.4A

By KCL, I= I₁₀₀ +I₇₀ = 1.4 +2 = 3.4 A

Let R_P be the equivalent of parallel combination of 70 and 100Ω

R_p = 70 × 100/ 70 + 100 = 41.2 Ω

50 Ω and 41.2 are in series.

R_total = 50 + 41.2 = 91.2 Ω

V = IR_total

= 3.4 × 91.2

= 310 volts

Ans : V = 310 volts

 

Example 3 Determine the equivalent resistance of the circuit of fig 1.28. between A and B.

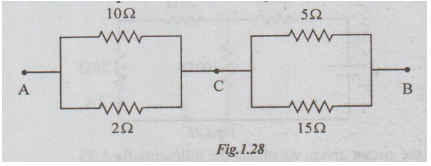
Solution: Step: 1

R_P2 = 10 || 2

= 10 × 2/10 + 2 = 20/12

= 1.67Ω

Step: 2

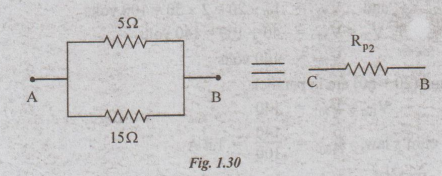
R_P2 = 5||15 = 5×15/5 + 15 = 3.75Ω

Step 3: R_P1 and R_P2 are in series,

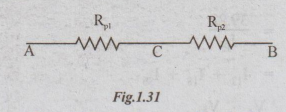
R_AB = R_AC + R_CB =R_P1+ R_P2=1.67 +3.75

Ans: R_AB = 5.42 Ω

 

Example 4 A circuit consisting of three resistances 12 Ω 18Ω and 36Ω respectively joined in parallel is connected in series with a fourth resistance. The whole circuit is applied with 60 V and it is found that the power dissipated in the 12Ω resistor is 36 W. Determine the value of the fourth resistance and the total power dissipated in the circuit.

Solution:

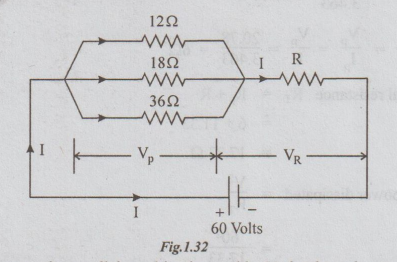
Let V_P be the voltage across the parallel combination and let V_R be the voltage across R.

Given that power dissipated in 12 Ω = 36 watts.

V_P = √36 × 12 = 20.78 volts.

V_R = 60-20.78

= 39.22 volts

For R, applying ohm's law,

Substituting I_R in (iii),

R = 39.22 /3.463 = 11.33Ω

and R_P = V_p/I_P = V_P/I = 20.78/3.463 = 6Ω

 Total resistance R_T = R_P + R

= 6 + 11.33

= 17.33Ω

Total power dissipated = V²/R_T

= 60²/17.33

= 208 watts

Ans: (i) R = 11.33Ω

 (ii) Total power dissipated = 208 watts

 

Example 5 Determine the value of R if the power dissipated in 10 ohm resistor is 40 W for the circuit shown.

Solution:

 

Example 6 The current in the 6Ω resistor of the network shown in the figure is 2A. Determine the currents in all other resistors and the voltage Vacross the network.

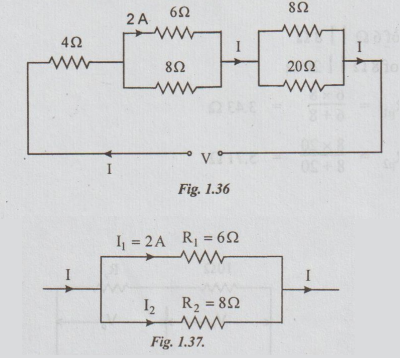
Solution: For parallel combination of 6 Ω and 8 Ω, applying current division formula we get

 

Example 7 In the circuit shown in the fig, the total power dissipated is 488 watts. Determine the current in each resistor and the p.d between A and B.

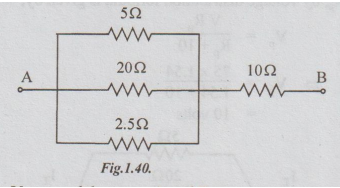
Solution:

Let V = p.d. between A and B

and R_T = total resistance between A and B

By applying ohm's law for each resistor in parallel branch, we get the currents as follows:

I₅ = 10/5 = 2A

I₂₀ = 10/20 = 0.5A

I₂₅ = 10/2.5 = 4A

Ans: 1₅ = 2A; I₂₀ = 0.5 A; I₂₅ = 4A; I₁₀ = 6.5 A

 

Example 8 If the total power dissipated in the circuit shown is 18 watts, find the value of R and current through it.

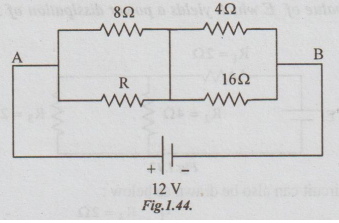
Solution: The given circuit can be re-drawn as shown below, for better understanding

Example 9 Find the value of E which yields a power dissipation of 50W in R3 of the following circuit.

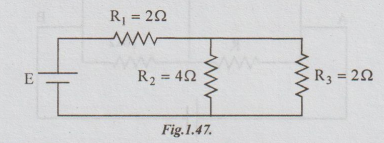
Solution: The original circuit can also be drawn as below:

 

Example 10 Two coils connected in parallel across a 100 v.d.c. supply draw a total current of 9A. The power dissipated in one resistor is 500 watts. Find the resistance of two coils and current in each coil.

Solution: Data:

V =100 volts

I = 9A

P₁ = 500 watts

R₁ and R₂ are in parallel.

R_T  = V/I = 100/9 = 11.11Ω ...(a)

R₁ R₂/R₁+ R₂ = 11.11

 

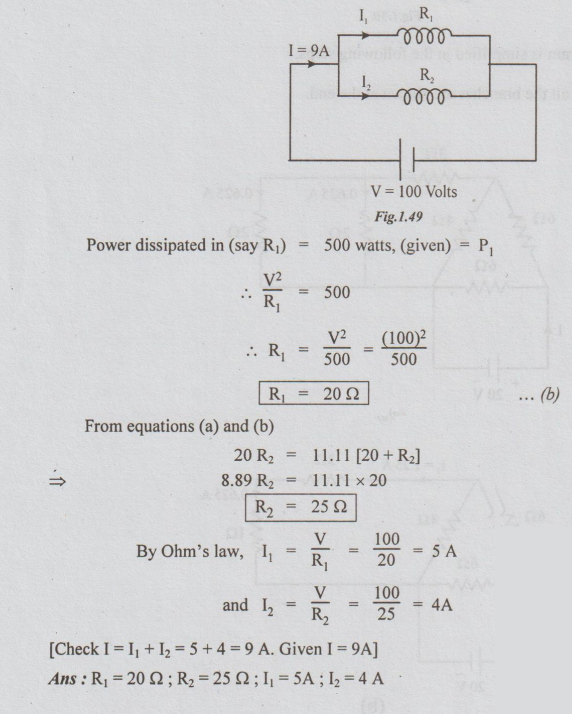
Example 11 Find the current supplied by the source in the circuit shown in the fig. Also determine the power in each resistor.

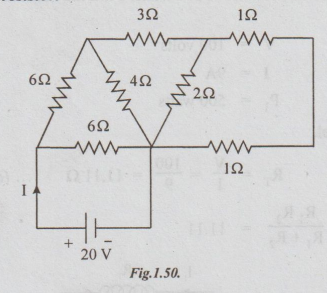
Solution: The circuit diagram is simplified in the following steps.

Note: The currents in all the branches are shown at the end.

Step 1:

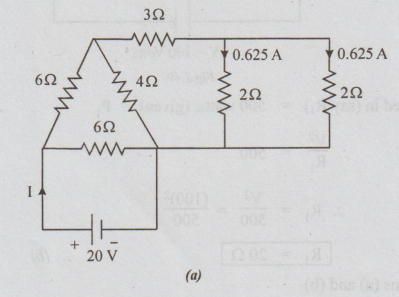
Step 2:

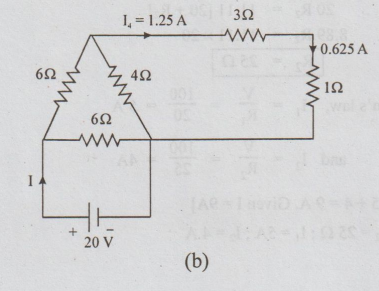
Step 3:

Step 4:

Step 5: Fig.1.53 (e), I₁ = 20/6 = 3.33A

I₂ = 20/8 = 2.5A

 I = I₁+I₂

= 3.33+2.5

= 5.83A

Power dissipated in 6Ω = I₁² × 6

= (3.33)² × 6

= 66.53 watts

The power dissipated in another 6Ω resistor

= I₂² × 6

=(2.5)2 × 6

= 37.5 watts

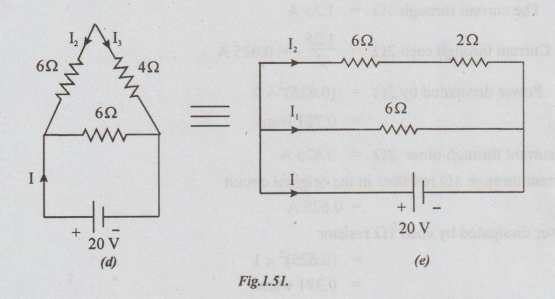
Represent I₂ in figs 1.53 (d) and (c)

Refer fig (c), 4Ω and 4Ω are in parallel [equal-resistances]

I₄ = I₂/2 = 2.5.2

= 1/25A

Power dissipated in 4Ω = (1.25)² × 4 = 6.25 W

Current through another 4Ω =1.25 A

Transfer this current to the fig (b). Refer fig. (b).

Current through 3Ω  = I₄

Power dissipated by 3Ω= (1.25)²×3=4.6875 watts.

See the 30 in fig (a).

The current through 3Ω  = 1.25A

Current through each 2Ω = 1.25/2=0.625A

Power dissipated by 2Ω = (0.625)² × 2 = 0.781 watts.

The current through other 2Ω = 0.625 A

 Current through 1Ω resistors in the original circuit = 0.625A

 Power dissipated by each 122 resistor

= (0.625)² × 1= 0.391 watts

Answers as tabulation:

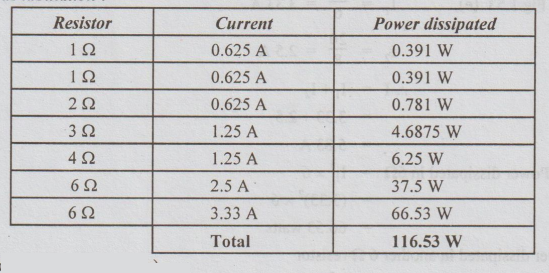
Note: For the circuit in fig. (e),

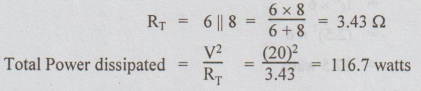
Check: Sum of power dissipated by all resistors = 116.53 watts

 

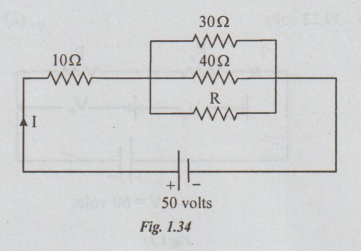
Example 12 Calculate the equivalent resistance of the following combination of resistors and also the source current.

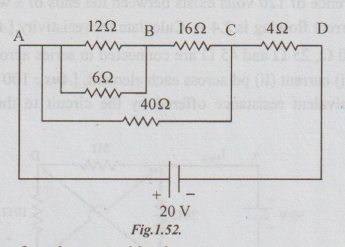
Solution: Start simplifying from inner combination.

Step 1: Replace parallel combination of 12 and 6Ω to get the following circuit.

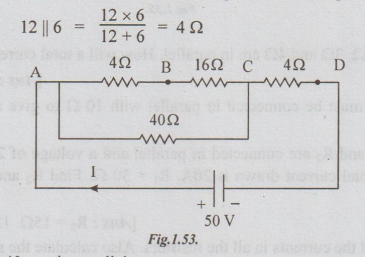
Step 2: (4+16) and 40 are in parallel.

Their equivalent resistance is =20 × 40/20 + 40 =13.3 Ω

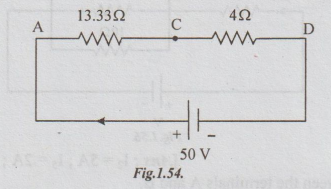
Step 3: 13.33 and 4 are in series.

R_T = R_AB = 13.33 +4

=17.33 Ω

Step 4: I = source current

= V/ R_T = 50/17.33 = 2.885 A

Ans: (i) R_T = 17.33Ω ; (ii) Source current I = 2.885 A