Electric Circuit Analysis: Unit V: Resonance and coupled circuits
Worked examples on series resonance
Electric Circuit Analysis: Unit V: Resonance and coupled circuits : Worked examples On series resonance
WORKED EXAMPLES
ON SERIES RESONANCE
Example
1 A series RLC circuit with R = 102, L = 1 mH and C = 1000 picofarads is
connected across a sinusoidal source of 20V with variable frequency (a) Compute
the resonant frequency of the circuit (b) Find the Q factor of the circuit at
the resonant frequency, (c) Determine the half power frequencies.
Solution:
Given R = 10 Ω, L= 1 mH, C = 1000 pF, E = 20 V

Example
2 A series RLC circuit with Q = 250 is resonant at 1.5 MHZ. Find the
frequencies at half power points and also band width.
Solution:
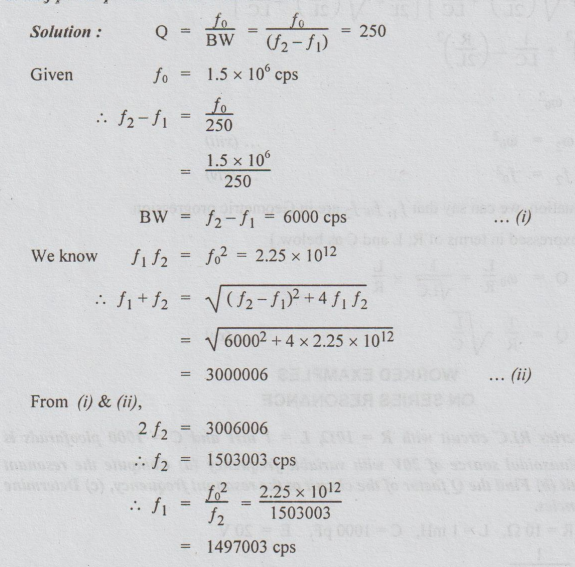
Example
3 A coil of resistance 2 Ω and inductance 0.01 H
is connected in series with a capacitor C. If maximum current occurs at 25 Hz
find C.
Solution:
When the current is maximum the circuit is at resonance. Therefore, the given
frequency is resonance frequency.
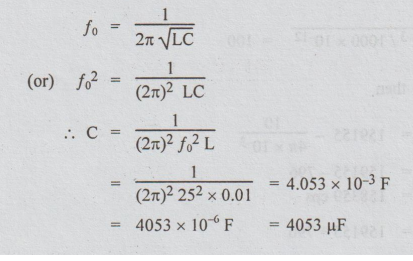
Example
4 What is the resonant frequency and Bandwidth of a series RLC circuit given R
= 552, L=40 mH, C=1 μF.
Solution:
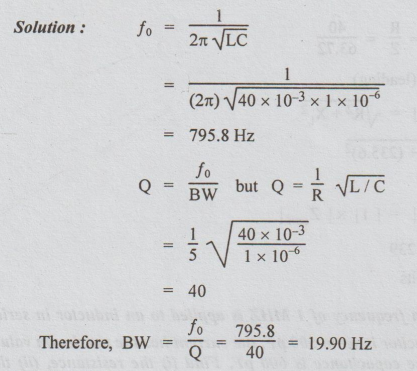
Example
5 A coil of resistance 402 and inductance 0.75 H forms part of a series circuit
for which the resonant frequency is 55 c/s. If the supply is 250V, 50 c/s find
(i) the line current, (ii) the p.f., (iii) voltage across the coil.
Solution:
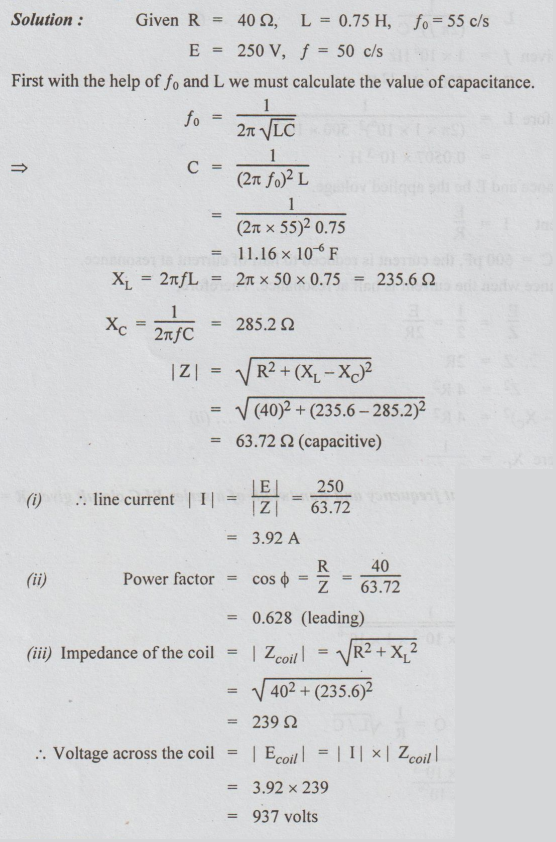
Example
6 A constant voltage at a frequency of 1 MHZ is applied to an inductor in
series with a variable capacitor. When the capacitor is set to 500 pF, the
current has the maximum value, while it is reduced to one half when the
capacitance is 600 pF. Find (i) the resistance, (ii) the inductance, (iii) the
Q factor of the inductor.
Solution:
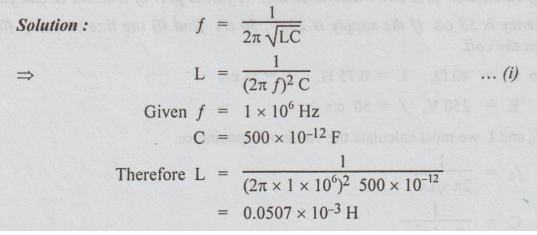
Let
R be the resistance and E be the applied voltage.
At
resonance, current I = E/R
Given
that, When C = 600 pF, the current is reduced to half of current at resonance. Let
Z be the impedance when the current is half at resonance. Therefore,
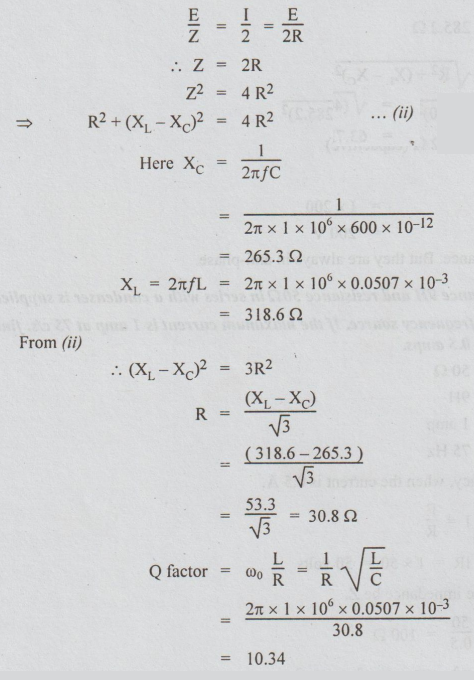
Example
7 A series RLC circuit has R = 2002, L = 20mII and C = 0.5uF. Calculate the
maximum current in the circuit and voltage across L and C for an input voltage
200 ∠
0°V.
Solution:
Since the current is maximum, the circuit is at resonance.

Note:
|EL| = | Ec| at resonance. But they are always in
anti-phase.
Example
8 A coil of inductance 9H and resistance 502 in series with a condenser is
supplied at constant voltage from variable frequency source. If the maximum
current is 1 amp at 75 c/s, find the frequency when the current is 0.5 amps.
Solution:
Given: R = 50 Ω
L
= 9H
Maximum
current = 1 amp
F0
= 75 Hz
It
is required to find the frequency, when the current is 0.5 A.
Maximum
current = I = E / R
E
= IR = 1 × 50 = 50 volts
When
the current is 0.5A, let the impedance be Z.

[Note: The student is advised
not to mistake the f1 and f2 as half power frequencies. Only for convenience we
have taken the symbols f1 and f2 for frequencies.]
6. Frequency at which Maximum Values of Ec and EL Occur
Case
(a): To find the frequency at which Ec is maximum.
The
voltage across the capacitor = | Ec|
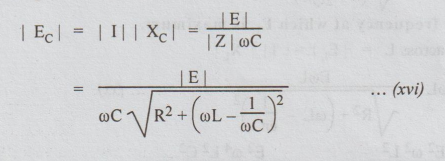
We
have to find out the frequency at which Ec is maximum i.e., at that frequency
dEc
/ d ω
= 0.
Before
differentiating the above equation, it is desirable to eliminate the radical
sign from the denominator. This can be done by differentiating E2 with respect
to o, since when E2 maximum Ec
will
also be maximum.
By
squaring equation (xvi), we get
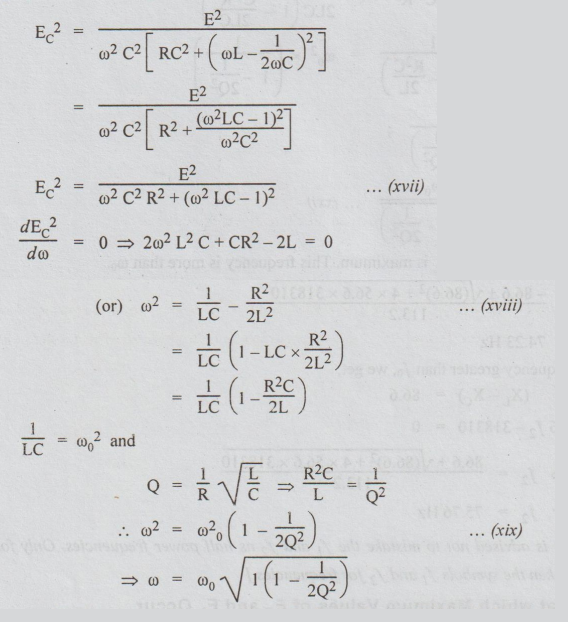
At
this frequency of o (in rad/sec) Ec is maximum. This ω is lesser than wc. From
the above equation,
we
say that at 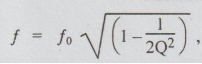 EC
maximum
EC
maximum
Case
(b): To find the frequency at which EL is maximum.
The
voltage across L = |EL| = |1| |XL|
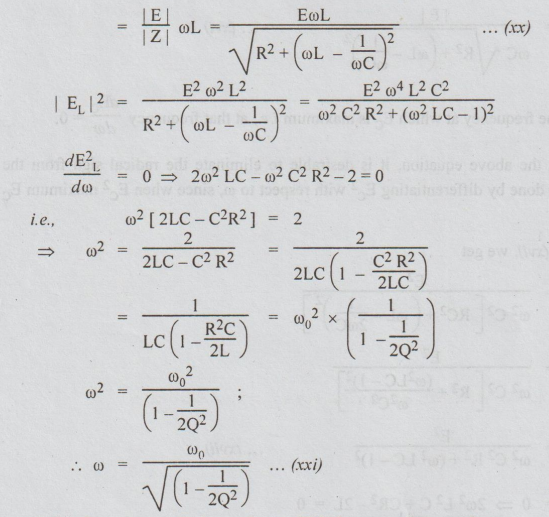
At
this frequency ω , ELis maximum. This frequency is more than ωo.
Example
9 A series circuit with R = 50 2; L = 0.05H and C = 20 micro farads has an
applied voltage of 100 ∠0°
with a variable frequency. Find the maximum voltage across the inductor as the
frequency is varied.
Solution:
Given : R 50Ω L = 0.05H
C
= 20 × 10-6 F; E = 100 ∠0o
volts.
Frequency
is variable.
The
frequency at which EL is maximum is given by the formula
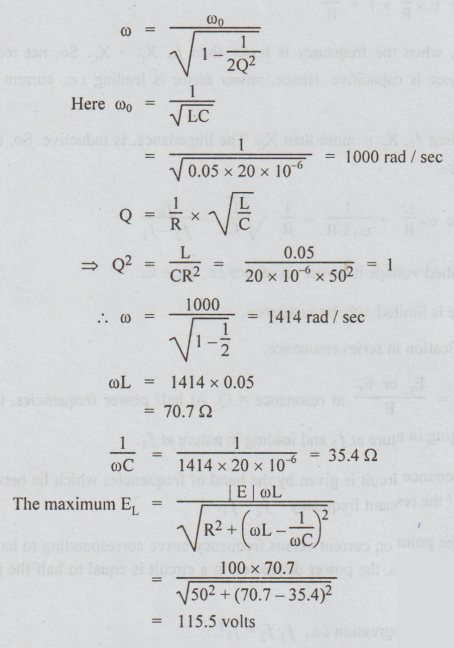
Electric Circuit Analysis: Unit V: Resonance and coupled circuits : Tag: : - Worked examples on series resonance
Related Topics
Related Subjects
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
