Worked Problems: AC circuits by nodal analysis method when ideal voltage source

WORKED PROBLEMS

[Note: On Nodal method when ideal voltage source is connected between two nodes]

Example 13 Find the current through the galvanometer in the circuit shown by nodal method.

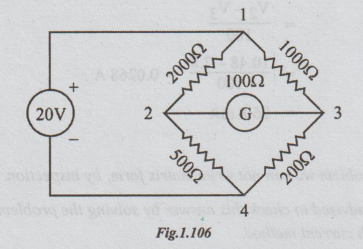
Solution: In this problem, the ideal voltage source is connected between two nodes. Take one of these nodes as reference. Preferably, the node to which the negative polarity of source is connected is taken as reference node. (say node 4). Then, the voltage of the other node (i.e., node 1) = V₁ = +20 volts.

Now by applying Kirchoff's current law we can get the simultaneous equations and find the node voltage. Finally, current can be found by applying ohm's law.

At node 2:

V₂ - V₁ / 200 + V₂ - V₄/ 500 +  V₂ - V₃ / 100 = 0

⇒ 5 (V₂ - V₁) + 2 (V₂ - V₄) + 10 (V₂-V₃) = 0

=>  5 (V₂ - 20)+ 2 (V₂- 0) + 10 (V₂ - V₃) =0

⇒ 17 V₂ - 10 V₃ = 100 ...(i)

Applying KCL at node 3, we get

(V₃ - V₁) / 1000 +  (V₃ - V₂) / 100 + (V₃ - V₄)/ 200 = 0

⇒ (V₃ - V₁) + 10 (V₃ - V₂)+ 5 (V₃ - V₄) = 0

 ⇒ (V₃-20) + 10 (V₃ - V₂) + 5 (V₃-0) = 0

⇒ -10 V₂ + 16 V₃ = 20

⇒ -V₂ + 1.6 V₃ = 2 ....(ii)

Adding (i) and (ii), we get

17.2 V₃ =134

 V₃ =7.8 volts

V₂ = 1.6 V₃ - 2 = 1.6 (7.8) - 2

=12.48 - 2

= 10.48 volts

The current through galvanometer = I_G

= V₂ - V₃ /100

= 10.48 - 7.8 / 100 = 0.0268 A

= 26.8 mA

[Note:

 (i) In the above problem we can not write matrix form, by inspection:

(ii) The student is advised to check this answer by solving the problem by either branch current method or mesh current method.

(iii) The same method is applicable for A.C. circuits with ideal voltage source]

Example 14 Draw a possible network having the following nodal equations and determine the nodal voltages.

7V₁ - 3V₂ - 4V₃ = -11

-3V₁ + 6V₂ - 2V₃ = 3

-4V₁ - 2 V₂+ 11V₃ = 25

Solution: The nodal equations in the matrix form are as:

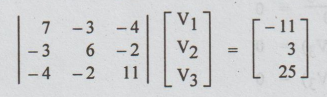
For the above nodal equations the circuit is as drawn below. All the passive elements are admittances measured in ohms.

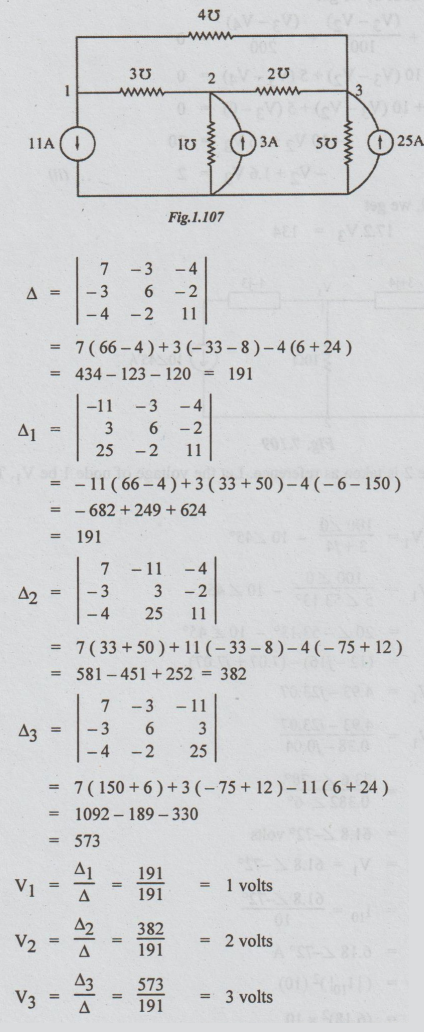
V₁ =  Δ₁ / Δ   = 191 / 191 = 1 volts

V₂  = Δ₂ / Δ = 382 / 191 = 2 volts

V₃ = Δ₃ / Δ = 573 / 191 = 3volts