Probability and complex function: Unit V: Ordinary Differential Equations
(a) Problems based on cauchy-euler
Solved Example Problems | Ordinary Differential Equations
Probability and complex function: Unit V: Differential equations : Example
III. (a) problems
based on cauchy-euler
Example 5.3.1. Solve 2 d2y/dx2
– x dy/dx + y = 0 [A.U. April 2002, M/J 2009] [A.U N/D 2002] [A.U Jan.
2016 R15, U.D MA 7151] [A.U A/M 2019 R17]
Solution: Given:
[x2 D2 - xD + 1]y = 0
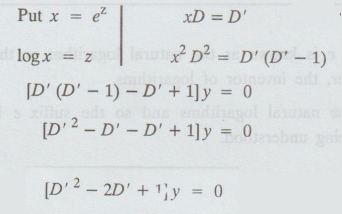
The
auxiliary equation is m2 - 2m+1 = 0
(m
− 1)2 = 0
m
=1, 1
y
= (Az + B) ez
=(A
log x + B) x [ x= ez, z = log x ]
y
= = x [A logx + B]
Note:
The independent solutions are x, x logx
Example 5.3.2. Solve x d2y/dx2
+ dy/dx = 0 [A.U. Nov. 2001] [A.U M/J
2005] [A.U Tvli. Jan 2008, Tvli M/J 2009] [A.U N.D 2014 R-13]
[A.U N/D 2019, R-17]
Solution: Given:
x D2y+ Dy = 0
x2
D2y + x Dy = 0 [Multiply by x]
[x2
D2 + xD] y = 0
Put
x =ez
Convert
xy'' + y' = 0 into a linear differential equation with constant coefficients
Ans.
upto equation(1)
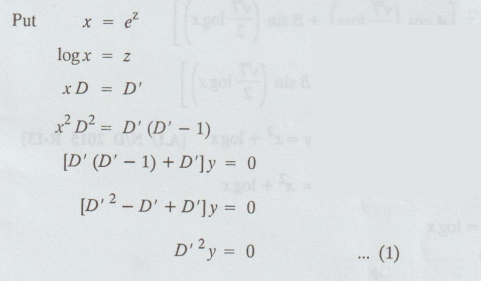
The
auxiliary equation is m2= 0, m= 0, 0
y
= [Az + B] e0z [ since, e0z = 1]
=
Az + B
y
= A (logx) + B
Example 5.3.3. Solve x2y'
+ 2xy' + 2y = 0 [AU, May 2001]
Solution: Given:
[x2 D2 + 2xD + 2] y = 0 .... (1)
Put
x = ez
logx
= z
x
D = D'
x2
D2 = D' (D' — 1)
(1)
⇒ [D' (D' - 1) + 2D' +
2] y = 0
[D'2
- D' + 2D' + 2] y = 0
[D'2
+ D' + 2]y = 0
The
auxiliary equation is m2 + m + 2 = 0
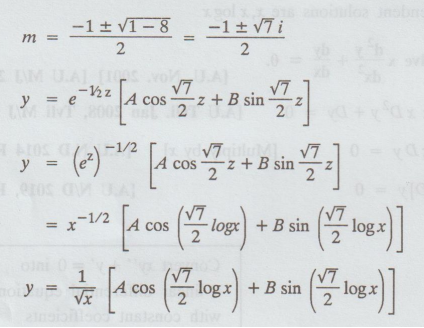
Example 5.3.4. Solve : x2y'' - 4xy'
+6y = x2 + logx [A.U N/D 2015 R-13]
Solution:
Given (x2 D2 - 4x D +6)y = x2 + log x
Put
x = ez, z = log x
X
D = D'
x2
D2 = D' (D' - 1)
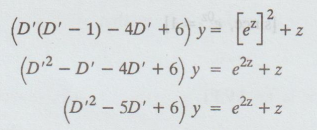
The
auxiliary equation is m2 - 5m + 6 = 0
(m-2) (m-3) = 0
m=2,
m = 3
C.F
= Ae2z + Be3z
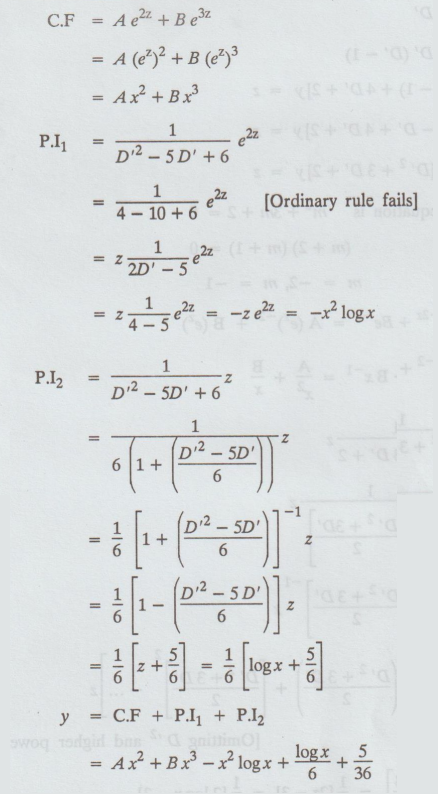
y
= C.F + P.I1+ P.I2
=
Ax2 + Bx3 - x2 log x + logx6 /6 + 5/36
Example 5.3.5. (x2D2
+ 4x D + 2) y = log x, given that when x= 1, y = 0 and dx/dy = 0.([Note: This
is an I.V.P] [A.U. March, 1996][A.U N/D 2013]
Solution:
Given: [x2 D2 + 4xD + 2]y = logx
Put
x =ez
logx
= z
xD
= D'
x2D2
= D' (D' - 1)
[D'
(D' - 1) + 4D' + 2]y = z
[D'2
- D' + 4D' + 2]y = z
[D'2
+ 3D' + 2]y = z
The
auxiliary equation is m2 + 3m + 2 = 0
(m
+ 2) (m + 1) = 0

(i) Given: x = 1, y (1) = 0
(1) ⇒
y (1) = A + B + [2 log 1 - 3]
0
= A + B + 1 [0 − 3] [ log 1 = 0]
0
= A + B – 3/4
⇒ A+B .....(2)
(ii)
Given: x = 1, y' (1) = 0
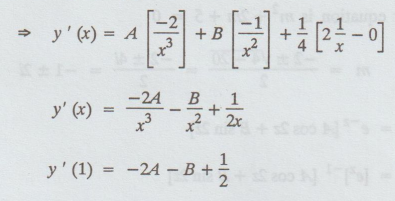
0
= - 2A – B + 1/2
2A
+ B = ½ ......(3)
(2)
– (3 ) ⇒ -A = ¾ - ½ = 1/4
A
= -1/4
(2)
⇒ -1/4 + B = 3/4
⇒ B = ¾ + ¼ = 4/4 =1
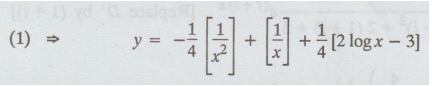
Example 5.3.6. Solve the equation (x2D2
+ 3xD+5) y = x cos (log x) [A.U M/J 2009]
Solution:
Given: (x2 D2 + 3x D + 5) y = x cos (log x).....(1)
Put
x =ez
log
x = z⇒ z = log x
xD
= D' where D' = d/dz
x2
D2 = D' (D' -1)
(1)
⇒ [D' (D' - 1) + 3D' +
5] y = ez cos (z)
[D'2
- D' + 3D'+5]y = ez cos z
[D'2 + 2D' + 5]y = ez
cos z
The
auxiliary equation is m2 + 2m + 5 = 0

i.e.,
P.I = 7/65 x cos (log x) + 4/65 x sin (log x)
Example 5.3.7. Solve [x2
D2 - xD + 1] y = [log x/x]2 [A.U April 02, N/D 07] [A.U
M/J 2014] [A.U N/D 2018 R-17]
Solution:
Given: [x2 D2 - xD + 1] y = [log x/x]2
Put
x = ez
log
x = z
xD
= D'
x2
D2 = D' (D' − 1)
[D' (D' - 1) - D' + 1] y = [z/ez]2
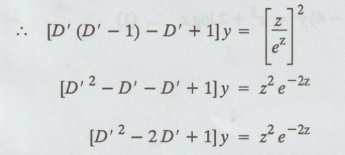
The
auxiliary equation is m2 - 2m + 1 = 0
(m
- 1)2 = 0
m
= 1, 1
C.F
= (Az + B) ez = (A log x + B)x
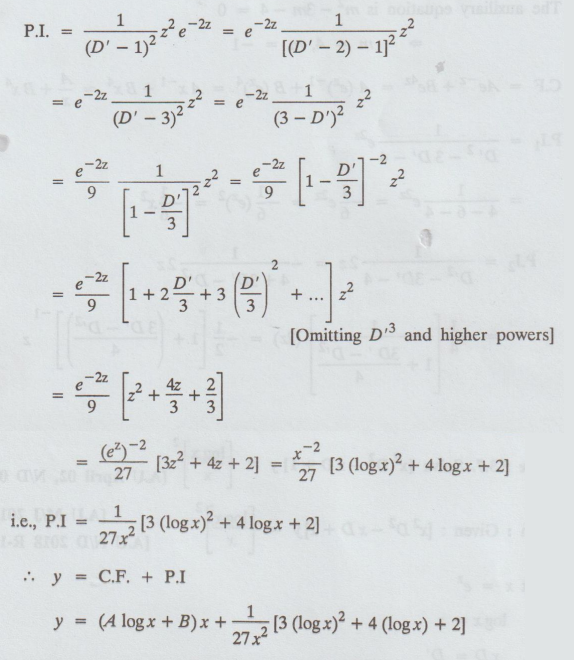
Example 5.3.8. Solve (x2D2
- 2xD - 4) y = x2 + 2log x[AU, May 1998] [A.U M/J 2010]
Solution:
Given: (x2D2 - 2xD - 4) y = x2 + 2 logx
.....(1)
Put
x = ez
log
x = z
x
D = D'
x2
D2 = D' (D' - 1)
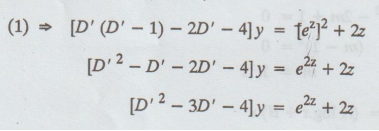
[D'z - 3D' - 4]y = e2z +
2z
The
auxiliary equation is m2 - 3m - 4 = 0
m
= 4, m = -1

y
=A/x + Bx4 – 1/6x2 – log x + 3/8
Example 5.3.9. Solve d2y/dx2
+ 1/x dy/dx = 12 log x/x2 [ A.U N/D 2012]
Solution:
Given: d2y/dx2 + 1/x dy/dx = 12 log x/x2
i.e.,
x2 d2y/dx2 + x dy/dx = 12 log x
i.e.,[
x2D2 + xD] = 12 log x ......(1)
put
x = ez
log
x = z
xD
= D'
x2
D2 = D' (D' - 1)
[D'
(D' - 1) + D']y = 12z
[D'2
- D' + D']y = 12z
(D')2y
= 12z
The
auxiliary equation is m2 = 0
C.F
= (Az + B) e0z = Az + B = A logx + B
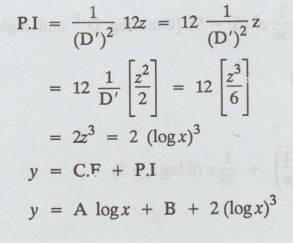
=
2z3 = (logx)3
y
= C.F+ P.I
y
= A log x + B + 2 (logx)3
Example 5.3.10. Solve (x2
D2 + 4xD + 2) y = x log x [A.U M/J 2016 R-8]
Solution:
Given: (x2 D2 + 4xD + 2) y =x log x .....(1)
put
x =ez
z
= log x
xD
= D'
x2
D2 = D' (D' - 1)
[D' (D' - 1) + 4D' + 2]y = ez z
[D'2
+ 3D' + 2]y = zez
The
auxiliary equation is m2 + 3m + 2 = 0
⇒ m =-2, m = -1
C.F
= Ae-2z + Be-z
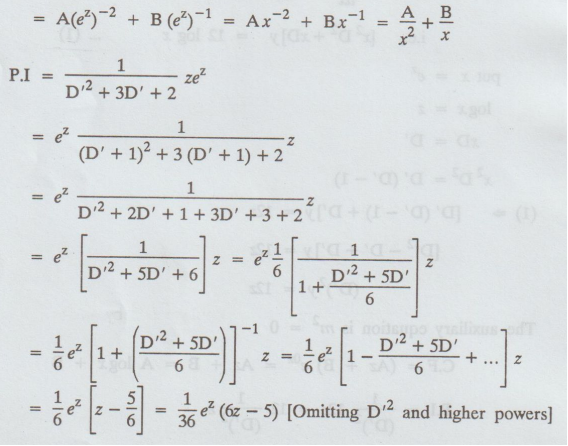
=
1/36 x (6 log x - 5)
y = C.F + P.I
(i.e.,)
y = A (1/x2) + B (1/x) + 1/36 x (6 logx - 5)
Example 5.3.11. Solve : (x2
D2 - xD + 1) y = sin (log x)[A.U N/D 2014 R-13]
Solution: Given:
(x2 D2 - xD + 1) y = sin (log x)
Put
x = ez
Z
= sin (log x)
xD=
D'
x2
D2 = D' (D' - 1), where D' = d/dz
(1)
⇒ (D' (D' - 1) - D' + 1)
y = sin z
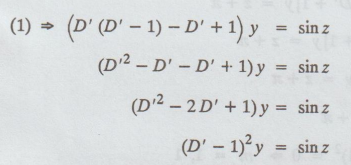
The
auxiliary equation is
(m
− 1)2 = 0
i.e.,
m = 1, 1
C.F
= (Az + B) ez
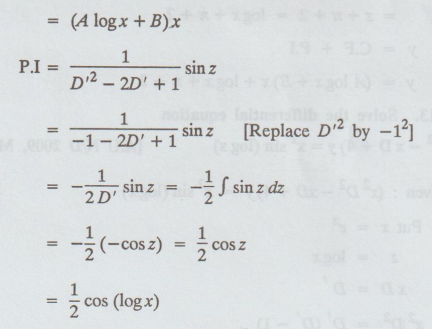
The
general solution is
y
= C.F + P.I
=
(A logx + B)x + ½ cos (logx)
Example 5.3.12. Solve : x2
d2y/dx2 – x dy/dx + y = log x + π [A.U A/M 2015 R13] [A.U
N/D 2016 R-13]
Solution: Given: [x2D2
- xD + 1]y =log x + π
Put
x = ez
Log
x = z
So that xD = D'
x2
D2 = D' (D' — 1)
=
[D' (D' - 1) - D' + 1]y = z + π
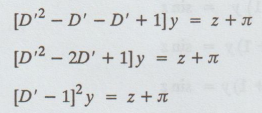
The
auxiliary equation is (m-1)2 = 0
m
= 1,1
C.F
= (Az + B)ez = (A logx + B) x
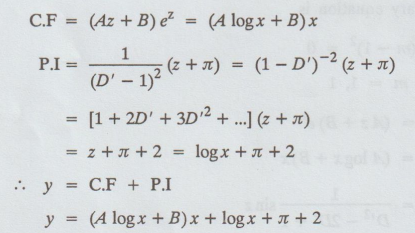
y
= C.F + P.I
y
= (A log x + B)x + log x + л + 2
Example 5.3.13. Solve the
differential equation (x2 D2 - xD + 4) y = x2
sin (log x) [A.U N/D 2009, M/J 2012]
Solution :
Given: (x2 D2 - xD + 4) y = x2 sin (log x).....(1)
Put
x = ez
z
= log x
xD
= D'
x2
D2 = D' (D' − 1)
(1)
⇒ [D' (D' − 1) − D' +
4]y = (ez)2 sin (z)
[D'2
- D' - D' + 4 ]y = e2z sin z
[D'2
- 2D' + 4]y = e2z sin z
The
auxiliary equation is m2 - 2m + 4 = 0
m2
- 2m + 4=0
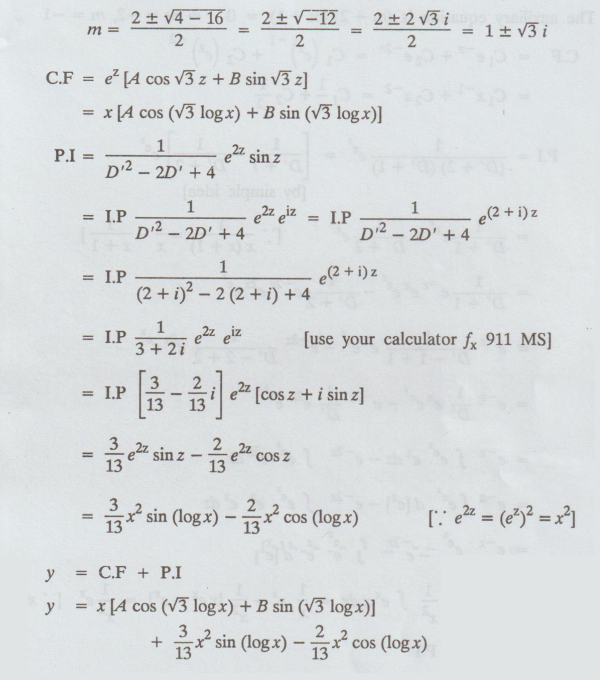
Example 5.3.14. Solve x2d2y/dx2
+ 4x dy/dx = ex [ A.U Tvli. A/M 2009 ]
Solution: Given: (x2
D2 + 4x D + 2) y = ex
Put
x = ez ⇒
logx
= z
So
that,
x
D = D'
x2
D2 = D' (D' - 1)
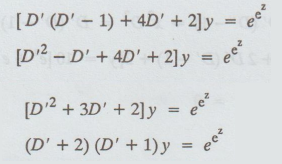
The
auxiliary equation is (m + 2) (m + 1) = 0 ⇒
m
= -2, m = -1
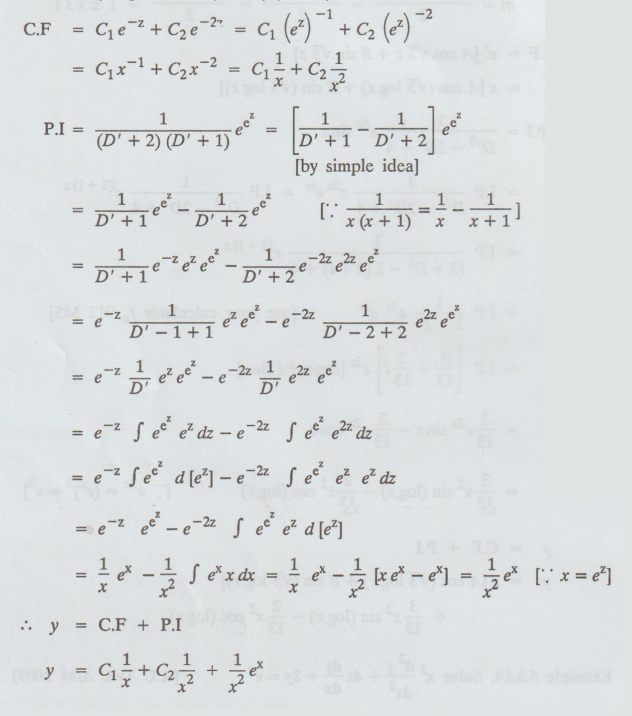
y
= C.F + P.I
y
= C11/x + C2 1/x2 + 1/x2 ex
Example
5.3.15. Solve x3d3y/dx3 + 2x2 d2ydx2
+ 2y = 10 [ x + 1/x ]
Solution : Given:
[x3 D3 + 2x2 D2 + 2]y = 10 [x + 1/x
]
Put
x = ez ⇒
logx
= z
So
that, x D = D' ⇒x2
D2 = D' (D' - 1) ⇒x3
D3 = D' (D' - 1) (D' - 2)
[D' (D' - 1) (D' - 2) + 2D' (D' - 1) + 2] y =
10 [ez + e-z]
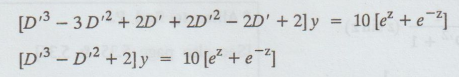
The
auxiliary equation is m3 - m2 + 2 = 0
m
= -1, m=1 ± i
C.F = C1e-z + ez
[C2 cos z + C3 sin z]=C1 (ez)-1 + ez
[C2 cos z + C3 sin z]
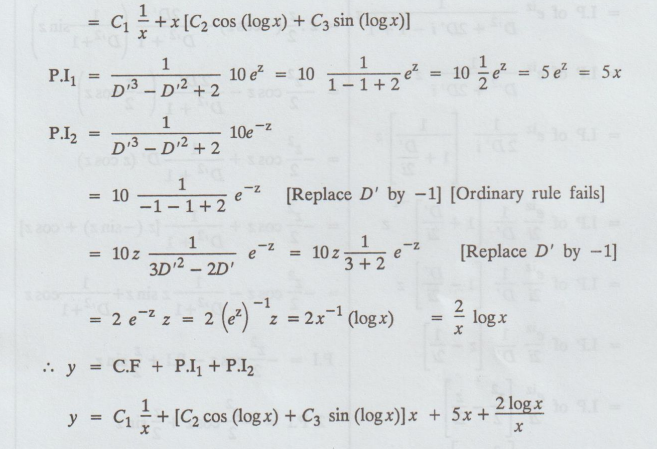
y
= C.F+ P.I1 + P.I2
y
= C1 1/x + [C2 cos (log x) + C3 sin (log x)]x
+ 5x + 2 log x/x
Example 5.3.16. Solve x2d2y/dx2
+ x dy/dx + y = log x sin (log x)
Solution:
Given: [x2 + D2 + xD + 1]y = log x sin (log x)
Put
x = ez ⇒z = log x
so
that, xD = D' , x2 D2 = D' (D' − 1)
[D'
(D' − 1) − D' + 1]y = z sin z
[D'2
- D' - D' + 1 ]y = z sin z
[D'2
+ 1 ]y = z sin z
The
auxiliary equation is m2 + 1= 0 ⇒m
= ±i

P.I
= − (logx)2 cos (log x)/4 + (logx) sin (log x)/4
y = C.F + P.I
Example 5.3.17. Solve x3d3y/dx3
+ 3x2d2y/dx2 + x dy/dx + 8y = 65 cos (log x)
Solution:
Given: [x3 D3 + 3x2 D2 + D + 8]y =
65 cos (log x)
Put
x = ez , z = log x
so
that, xD = D' , x2 D2 = D' (D' − 1)
x3
D3 = D' (D' − 1) (D' − 2)

Example 5.3.18. Solve : x2d2y/dx2
+ 2x dy/dx -12y = x3 log x
Solution: Given:
[x2 D2 + 2xD - 12]y =x3 log x
Put
x = ez
z
= log x
xD
= D'
x2
D2 = D' (D' − 1)
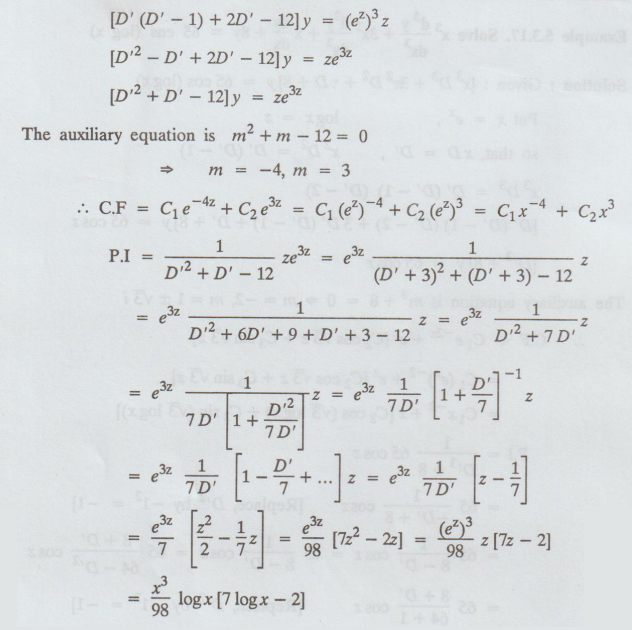
y
= C.F + P.I
y
= C1x-4 + C2x3 + x3/98 log
x [7 logx - 2]
Example 5.3.19. Solve x2d2y/dx2
- 3x dy/dx + 4y = (1 + x)2
Solution: Given:
(x2 D2 - 3xD + 4) y = (1+x)2
.......................(1)
Put
x = ez
z
= log x
xD
= D'
x2
D2 = D' (D' − 1)
(1)
⇒ [D' (D' − 1) − 3D' +
4]y = (1 + ez)2
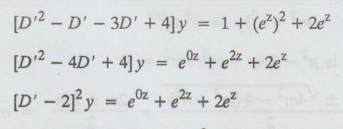
The
auxiliary equation is (m – 2)2= 0 , m = 2,2
CF
= (C1z + C2) e2z
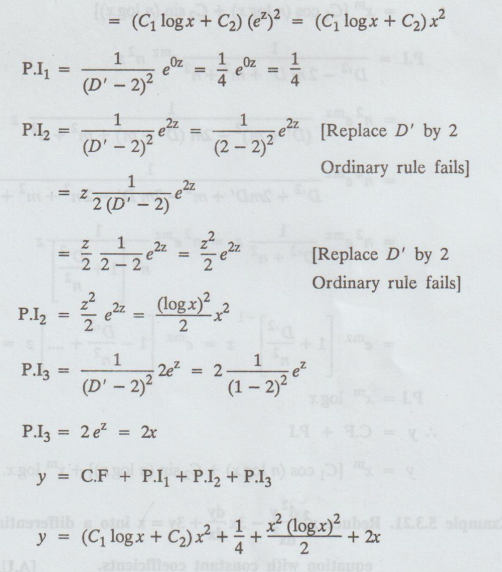
P.I3
= 2ez =2x
y
= C.F + P.I1 + P.I2 + P.I3
y
= (C1 logx + C2) x2 + 1/4 + x2 (log
x)2/2 + 2x
Example 5.3.20. Solve [x2D2
- (2m - 1) x D + (m2 + n2)ly = n2 xm
log x
Solution:
Given: [x2D2 - (2m - 1)xD + (m2 + n2)ly
= n2xm logx
Put x = ez , z = log x = z
xD
= D' , x2 D2 = D' (D' − 1)

Example 5.3.21. Reduce x2d2y/dx2
- 3x dy/dx + 3y = x into a differential
equation with constant coefficients. [A.U. N/D 2007]
Solution :
Given: x2d2y/dx2
- 3x dy/dx + 3y = x
i.e.,
[x2 D2 - 3xD + 3]y = x ... (1)
Put
x = ez
log x = z
xD
= D' , x2 D2 = D' (D' − 1)
(1)
⇒ [D' (D' − 1) − 3D' + 3]y
= ez
[D'2 - D' - 3D' + 3 ]y = ez
[D'2
- 4D' + 3]y =ez
Example 5.3.22. Write Euler's
Homogeneous linear differential equation. How will you convert it to a linear
differential equation with constant coefficients? [A.U. A/M. 2008]
Solution:
An equation of the forma
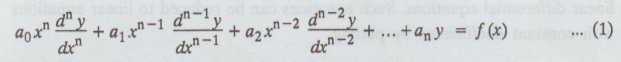
where
a0, a1, a2,+...+an..., an are
constants and f(x) is a function of x.
Equation
(1) can be reduced to linear differential equation with constant coefficients
by putting the substitution.
x = ez
(or) z = log x xD = D' , D' = d/dz
x2
D2 = D' (D' − 1), x3 D3 = D' (D' − 1) (D' − 2)
Example 5.3.23. TrAnsform (x2
D2 + xD + 1) y = 0 into differential equation with constant
coefficients, where D = d/dx [A.U. CBT M/J 2008 SM0101]
Solution:
Given: (x2 D2 + xD + 1) y = 0 .....(1)
Put
x = ez log x = z
xD = D' ; x2 D2 = D' (D'
− 1)
(1)
⇒ [D' (D' − 1) + D' + 1]y
= 0
[D'2
- D' + D' + 1 ]y = 0 ,[D'2 + 1]y = 0
5.3.23 (b) TrAnsform the equation
xy" + y' + 10 into a linear equation with constant co-efficients.
[A.U N/D 2018 R-17]
Solution: Given:
xy" + y' + 1 = 0
x2y" + xy' + x = 0
x2y"
+ xy' = -x ......(1)
Put
x = ez log x = z , xD = D', x2
D2 = D' (D' − 1)
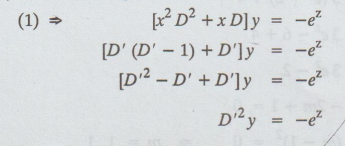
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (a) Problems based on cauchy-euler
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
