Problems based on method of variation of parameters

II. Problems based on method of variation of parameters

 

Example 5.2.1. Solve (D² + a²) y=  tan ax by the method of variation of parameters.  [A.U. M/J 2005, A/M 2008, N/D 2007] [A.U M/J 2009, M/J 2013]  [A.U N/D 2014] [A.U N/D 2016 R-15, A/M 2017 R-8] [A.U A/M 2019 R-17]

Solution: Given: (D² + a²) y = tan ax

The auxiliary equation is m² + a² = 0

m = ±ai

C.F = e^0x [C₁ cos ax + C₂ sin ax]

C.F = C₁ cos ax + C₂ sin ax

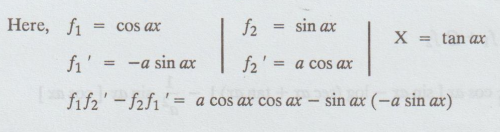
= a cos² ax + a sin² ax

= a[cos² ax + sin² ax]

P.I = P f₁  + Q f₂

= -1/a² [ cos ax lg ( sec ax + tan ax) ]

Y = C.F + P.I

y = C₁ cos ax + C₂ sin ax – 1/a² cos ax log [sec ax + tan ax]

 

Example 5.2.2 Solve (D²+ a²) y = a² tan ax by the method of variation of paramters.

Solution : Hint: In the Example 5.2.1

X = a² tan ax, we get

P = sin ax - log (sec ax + tan ax), Q = - cos ax

P.I = Pf₁ + Qf₂

Y = C.F + P.I

y = C₁ cos ax + C₂ sin ax - cos ax log [sec ax + tan ax]

 

Example 5.2.3. Solve d²y /dx² + 4y = 4 tan 2x using method of variation of parameters.  [A.U N/D 2014 R-13, D2015/Jan.2016]

Solution: Hint: In the Example 5.2.2 put a = 2, we get

y = (C₁ cos 2x + C₂ sin 2x) - cos 2x log (sec 2x + tan 2x)

 

Example 5.2.4. Solve: d²y/dx² + y = tan x by the method of variation of parameters.[A.U N/D 2003] [A.U M/J 2016 R-13]

Solution: Hint: In the Example 5.2.1 put a = 1, we get

y  = C₁ cosx + C₂ sinx – cos x log (sec x + tanx)

 

Example 5.2.5. Solve (D²+ a²) y = sec ax using the method of variation of parameters. [A.U. M/J 2012]

Solution: Given: (D² + a²) y = sec ax

The auxiliary equation is m² + a² = 0

m² = -a²

m = ± ai

C.F = C₁ cos ax + C₂ sin ax

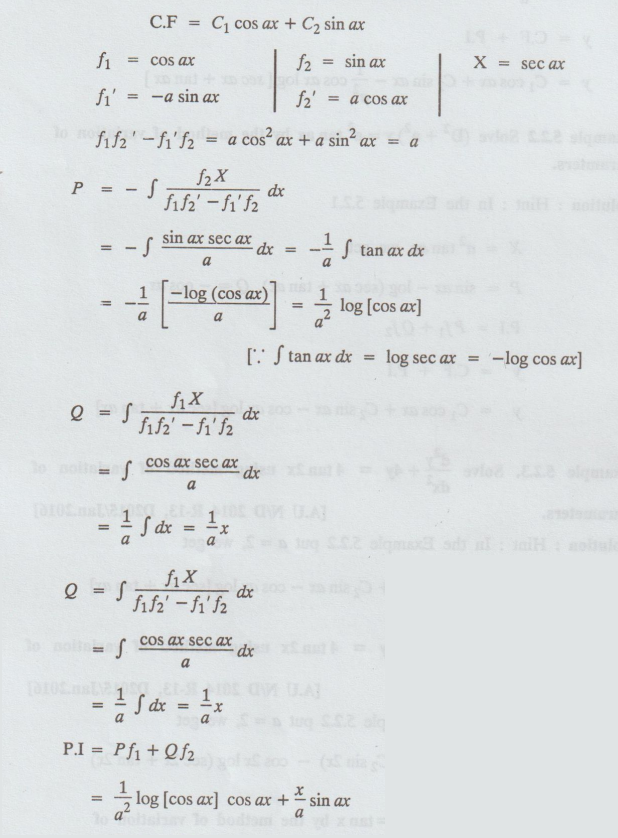
P.I= Pf₁ + Qf₂

= 1/a²log [cos ax] cos ax + x/a sin ax

 

Example 5.2.6. Use the method of variation of parameters to solve (D² + 1) y = sec x. [AU, Dec. 1999, A.U. A/M 2004, A.U(Trichy) J/J 2008] [A.U D15/J16 R-13] [A.U N/D 2016 R-13]

Solution: Hint: In the Example 5.2.5 put a = 1, we get

y = C₁ cosx + C₂ sinx + cos x log (cosx) + x sinx.

 

Example 5.2.7. Solve (D² + 4) y = sec 2 x by the method of variation of parameters. [AU, March 1996, AU Model, A.U. N/D 2002, CEG Nov. 2002] [A.U N/D 2010 R-8]

Solution: Hint: In the Example 5.2.5 put a = 2, we get

y = C₁ cos 2x + C₂ sin 2x + ¼ log [ cos 2x cos 2x + ½ x sin 2x

 

Example 5.2.8. Solve d²y/dx² + y = cosec x by using method of variation of parameters. [A.U N/D 2012] [A.U A/M 2011 R-8]  [A.U. N/D 2019, R-17]

Solution: Given: d²y/dx² + y = cosec x

i.e., (D² + 1) y = cosec x

The auxiliary equation is m² + 1 = 0

m = ± i

C.F. = C₁ cos x + C₂ sin x

Here,

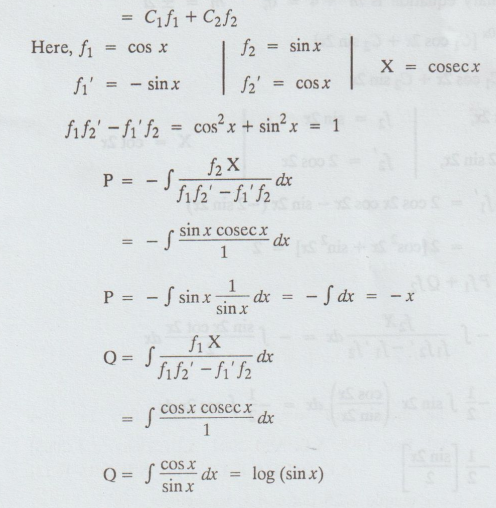
P.I = P f₁ + Q f₂

= -x cos x + log (sin x) sin x

y= C.F + P.I

 C₁ cos x + C₂ sin x = - x cos x + sin x log (sin x)

 

Example 5.2.9 Solve (D²+ a²) y = cosec ax by the method of variation of parameters.

Solution: Hint: f1f2' -f1'f2  = a

P = -x/a Q = 1/a² log ( sin ax)

y = C₁ cos ax + C₂ sin ax – x/a cos ax + 1/a² sin ax log (sin ax)

 

Example 5.2.10. Apply the method of variation of parameters to solve (D2 + 4) y = cot 2 x [A.U N/D 2009, N/D 2011] [A.U N/D 2015 R-13]

Solution: Given: (D² + 4) y = cot 2x

The auxiliary equation is m² + 4 = 0 ; m = ± 2i

C.F = e^0x [C₁ cos 2x + C₂ sin 2x]

C.F = C₁ cos 2x + C₂ sin 2x

Here ,

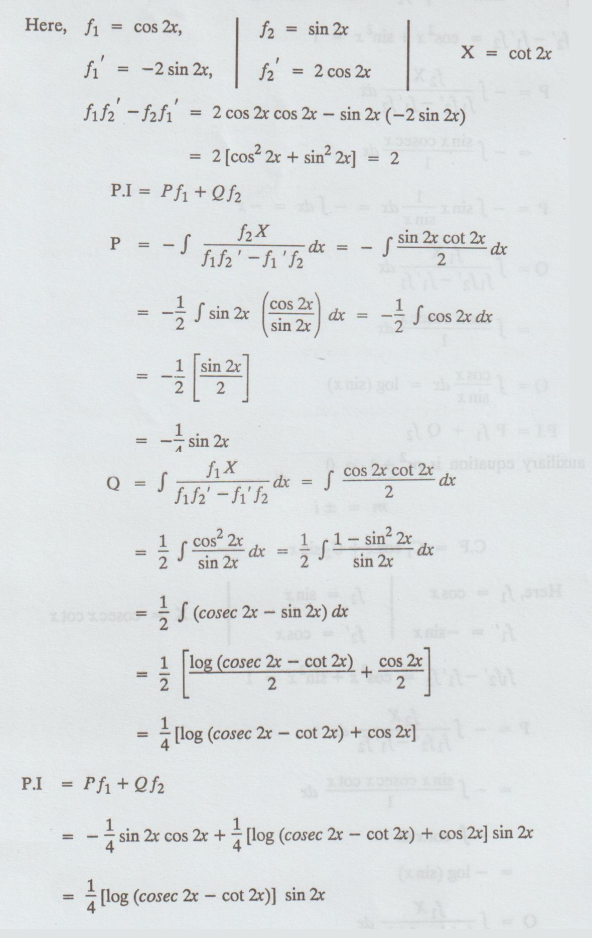
y = C.F + P.I.

= C₁ cos 2x + C₂ sin 2x + ¼  [log (cosec 2x - cot 2x)] sin 2x

 

5.2.11 Solve (D² + a²) y = cot ax by the method of variation of parameters.

Solution: Hint: f1f2' -f1' f2 = a

 

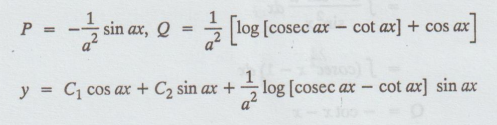
Example 5.2.12. Solve d2y/dx2 + y = cosec x cot x using the methd of variation of parameters. [A.U. N/D 2007] [A.U A/M 2015 R8]

Solution: Given: d2y/dx2 + y = cosec x cot x

i.e., (D² + 1) y = cosec x cotx

The auxiliary equation is m² + 1 = 0

m = ±i

C. F = C₁ cos x + C₂ sin x

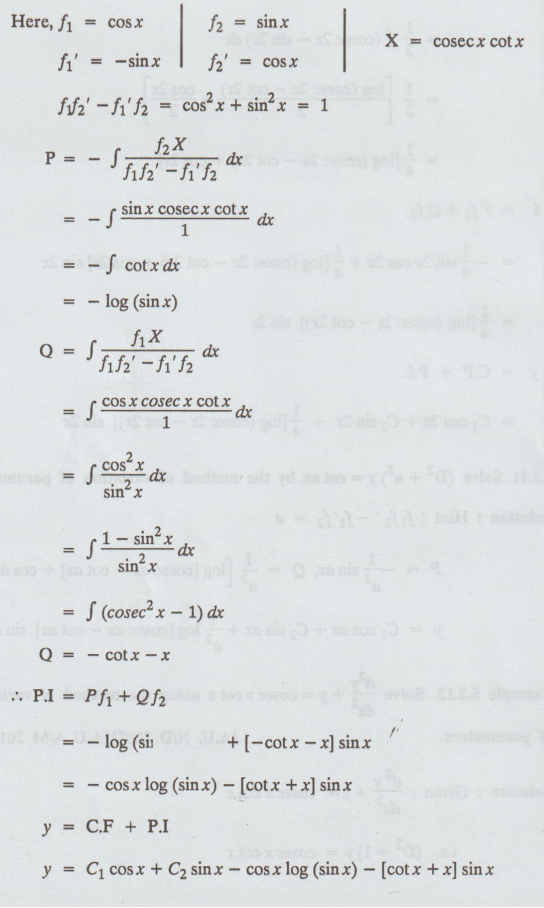
y = C₁ cosx + C₂ sinx – cosx log (sin x) – [cotx +x]sin x

 

Example 5.2.13. Solve by the method of variation of parameters d2y/dx2 + y = x sin x [A.U Nov. 2001, A.U Model Qn.] [A.U M/J 2010 R-8]

Solution: Given: d2y/dx2 + y = x sin x

ie., (D²+1) y = x sinx

The auxiliary equation is m² + 1 = 0

m = ±i

C. F. = C₁ cos x + C₂ sin x

= C₁f₁+ C₂f₂

Here,

y = A cos x + B sin x – x²/4 cos x + x/4 sin x , where A = C₁ + 1/8, B = C₂

Note: See also page no. 5.35 and 5.36

 

Example 5.2.14. Solve by method of variation of parameters y''= 4/x y' +4/x²y = x+ 1 [A.U. A/M 2008]

Solution: Given: y''= 4/x y' +4/x²y = x+ 1

i.e., x²y'' - 4xy' + 4y = x⁴ + x²

i.e., [x² D² - 4xD + 4]y = x⁴ + x²..........(1)

Put x = e^z

log x = log e^z

= z

So that, xD = D'

x²D² = D' (D' - 1)

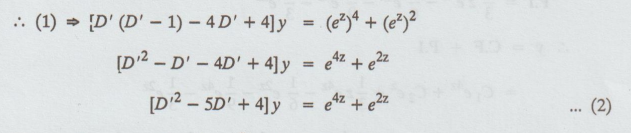
The auxiliary equation is m² - 5m + 4 = 0

(m-4) (m-1) = 0

m = 4, m = 1

C.F = C₁e^4z + C₂ e^z

Here

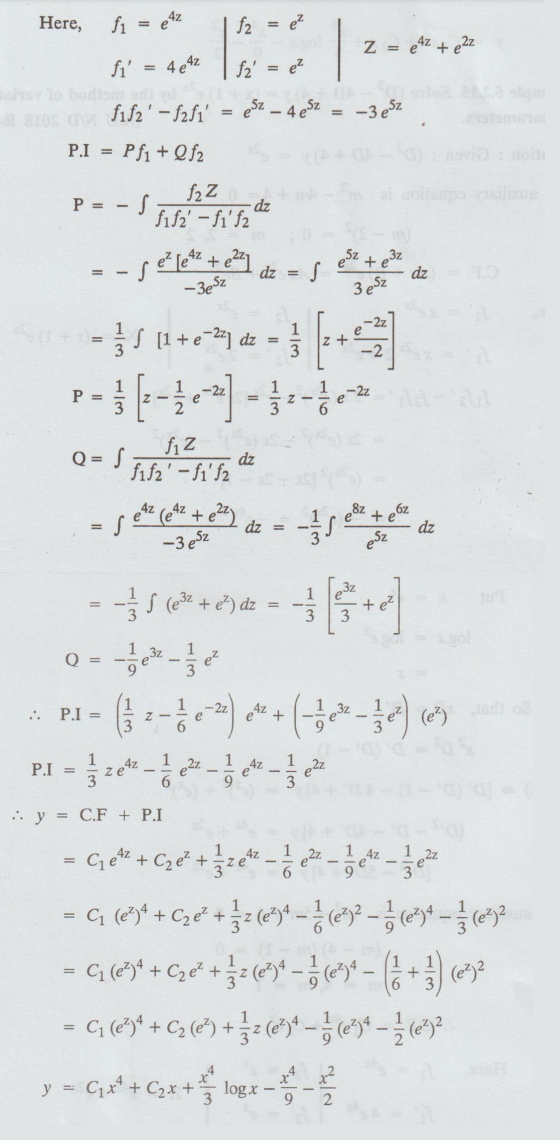
y = C₁x⁴ + C₂x+ x4/3 log x – x⁴/9 – x²/2+

 

Example 5.2.15. Solve (D² - 4D + 4) y = (x + 1) e^2x by the method of variation of parameters. [A.U N/D 2018 R-17]

Solution: Given: (D² - 4D + 4) y = e^2x

The auxiliary equation is m² - 4m + 4 = 0

(m-2)² = 0; m = 2,2

C.F = (Ax + B)e^2x  = Axe^2x + Be2x

Here

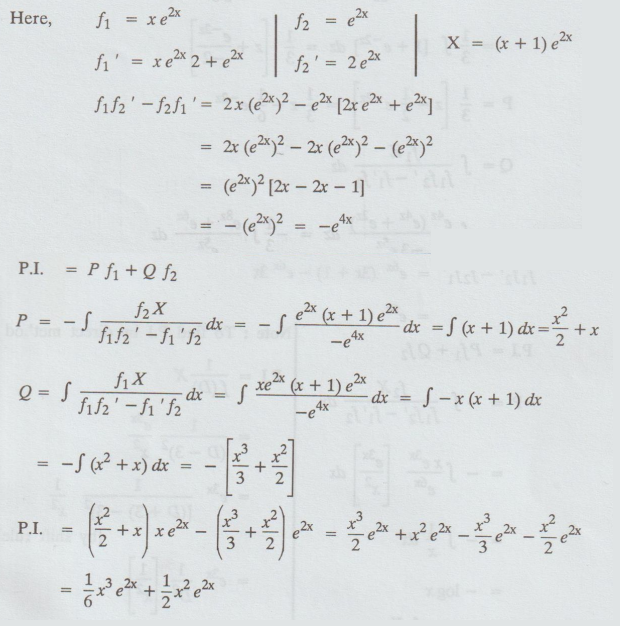
y = C.F + P.I.

y = (Ax + B) e^2x + 1/6 x³ e^2x + ½ x² e^2x

 

Example 5.2.16 Using the method of variation of parameters, solve  d²y/dx² – 6 dy/dx + 9y= e^3x /x²

Solution: Given: d²y/dx² – 6 dy/dx + 9y= e^3x /x²

i.e., D²y - 6Dy + 9y = e^3x/x²

[D² - 6D + 9] y = e^3x /x²

The auxiliary equation is m² - 6m +9 = 0

 (m − 3)² = 0; m = 3, 3

C.F = (C₁+ C₂x) e^3x

Here,

 

Example 5.2.17. Solve (D² + 2D + 5) y = e^-x tan x.

Solution: Given: (D² + 2D + 5) y =  e^-x tan x

The auxiliary equation is m² + 2m + 5 = 0

M = -2 ± √4 – 20 /2 = -1±  12i

C.F= e^-x [C₁ cos 2x + C₂ sin 2x]

= C₁e^-x cos 2x + C₂ e^-x sin 2x

= C₁f₁ + C₂f₂

Here

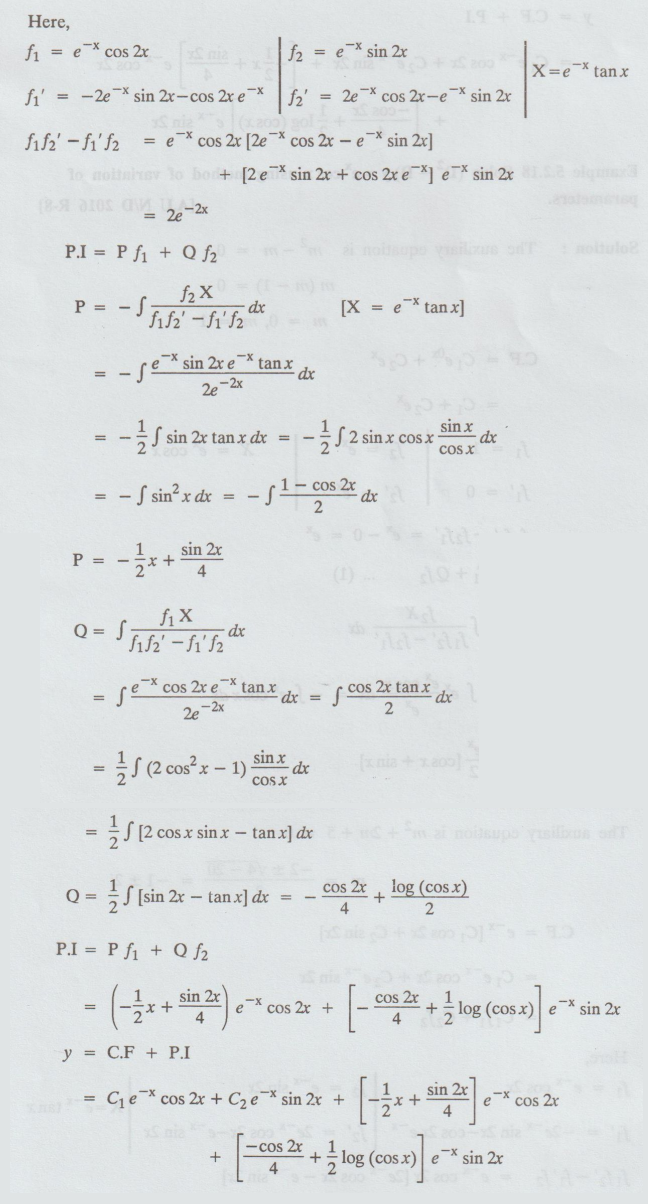
Example 5.2.18 Solve (D² - D) y = e^x cos x using method of variation of parameters. [A.U N/D 2016 R-8]

Solution : The auxiliary equation is m² - m = 0

m (m − 1) = 0

m = 0, m = 1

C.F = C₁e^0x + C₂ e^x

= C₁ + C₂e^x

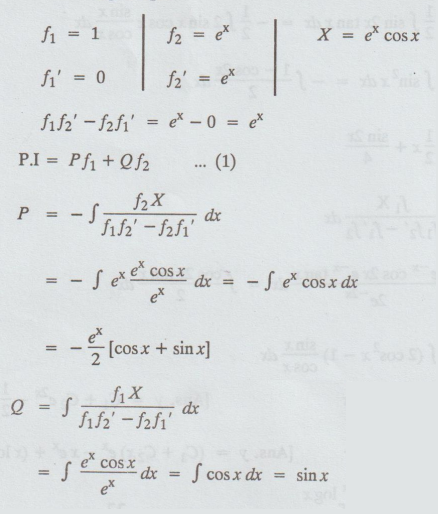
P.I = -e^x/2 [cos x + sin x ] + sin x e^x

y = C.F + P.I

y = C₁ + C₂ e^x -e^x/2 [cos x + sin x ] + sin x e^x