(a) Problems based on r.h.s. of the given differential equation is zero

I. (a) PROBLEMS BASED ON R.H.S. OF THE GIVEN DIFFERENTIAL EQUATION IS ZERO.

 

Example 5.1.1. (a) Solve (D² - 5D+6) y = 0

Solution: Given: (D² - 5D+6) y = 0

The auxiliary equation is m² - 5m + 6 = 0

i.e., m = 2, m = 3

C.F. = Ae^2x + Be^3x

The general solution is given by y = C.F

i.e., y = Ae^2x + Be^3x

 

Example 5.1.1(b) Solve (D² + 6D + 9) y = 0   [A.U M/J 2016 R-8]

Solution: Given: (D² + 6D +9) y = 0

The auxiliary equation is m2 + 6m + 9 = 0 ⇒ m = −3, m = −3

y =  C.F = (Ax + B) e^-3x

Note: Solving quadratic equations and cubic equations use your calculator f_x 991MS,

 

Example 5.1.1(c) Solve (D² + 2D + 1) y = 0  [A.U M/J 2014 R-13]

Solution: Given: (D² + 2D + 1) y = 0

The auxiliary equation is m² + 2m + 1 = 0 ⇒ m = −1, −1

y = (Ax + B)e^-x

 

Example 5.1.2. Solve d²y / dx² – 6 dy/dx +13y = 0.

[A.U N/D 2009, N/D 2003, M/J 2007]

Solution:

Given: d²y / dx² – 6 dy/dx +13y = 0.

The auxiliary equation is m² - 6m + 13 = 0  i.e.,(D² – 6D + 13) y = 0

Hence, the solution is y = e^3x [A cos (2x) + B sin (2x)].

 

Example 5.1.3 Solve (D² + 1) y = 0, given y (0) = 0, y' (0) = 1. [A.U April, 1996]

Solution :

Given: (D² + 1) y = 0

The auxiliary equation is m² + 1 = 0 ⇒ m² = -1 m = ± i

y = A cosx + B sin x

i.e., y (x) = A cos x + B sin x … (1)

Given: y (0) = 0 ⇒ y (0) = A = 0

y(x) = - A sin x + B cos x

Given: y' (0) = 1 ⇒ y' (0) = B = 1

(1) ⇒ y (x) = sin x

Note: The above problem is called an initial value problem (I.V.P), because all the conditions are given at a single point i.e., x = 0.

 

Example 5.1.4 (a) Solve (D² +1) y = 0 given y (0) = 1, y (π/2) = 0

Solution: Given (D² + 1) y = 0

The auxiliary equation is m² + 1 = 0 ⇒ m² = -1 m = ± i

y  = A cos x + B sin x

i.e., y(x) = A cosx + B sin x … (1)

Given y (0) = 1 ⇒ y (0) = A = 1

Given: y (π/2) = 0 ⇒ y (π / 2) = B = 0

 (1) ⇒ y (x) = cos x

Note: The above problem is called a boundary value problem (B.V.P), because the conditions are given at more than one point i.e., x = 0 and x = π/2

 

Example 5.1.4(b) Solve (D²+ D + 1) y = 0

 [A.U M/J 2016 R-13]

Solution: Given: (D² + D + 1)y = 0

The auxiliary equation is m² + m + 1 = 0 ⇒ m = -1/2 ± √3/2 i

 

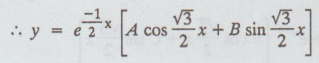
Example 5.1.5. Solve d³ y / dx³ – 6 d²y / dx² + 11 dy/dx – 6y = 0.

Solution: Given: d³ y / dx³ – 6 d²y / dx² + 11 dy/dx – 6y = 0.

i.e., (D³ – 6D² + 11D – 6) y = 0

The auxiliary equation is m³ - 6m² + 11m - 6 = 0

i.e., m = 1, m = 2, m = 3

All these roots are real and different.

Hence, the solution is y = Ae^x + Be^2x + Ce^3x

 

Example 5.1.6. Solve (D³ - 3D² + 3D - 1) y = 0 [A.U D15/J16 R-13]

Solution: Given: (D³ - 3D² + 3D - 1) y = 0

The auxiliary equation is m³ - 3m² + 3m - 1 = 0

i.e., m = 1 (thrice)

Hence, the solution is y = e^x [A+ Bx + Cx²]

 

Example 5.1.7 Solve (D³ + D² + 4D + 4) y = 0

[A.U A/M 2015 R-13]

Solution: Given: (D³ + D² + 4D + 4) y = 0

The auxiliary equation is m³ + m² + 4m + 4 = 0

⇒ m = -1, ± 2i

y = Ae^-x + e^0x [B cos 2x + C sin 2x]

= Ae^-x + B cos 2x + C sin 2x

 

Example 5.1.8 Solve : (D³ + 1) y = 0

 [A.U N/D 2018 R-17]

Solution: Given: (D³ + 1)y = 0

The auxiliary equation is m³ + 1 = 0

⇒ (m.+ 1) (m² - m + 1) = 0

 

Example 5.1.9. (a) Solve (D⁴ + 4D³ + 8D² + 8D + 4) y = 0.

Solution: Given: (D⁴ + 4D³ + 8D² + 8D + 4) y = 0

The auxiliary equation is

m⁴ + 4m³ + 8m2 + 8m² + 4 = 0

(m²) ² + (2m) ² + (2) ² + 2 (m²) (2m) + 2 (2m) (2) + 2 (2) (m²) = 0

[a² + b² + c² + 2ab + 2 bc + 2 ca = (a + b + c) ²]

⇒ (m² + 2m + 2) ² = 0

m = -2 ± √ 4 – 8 = -1 ± i (twice)

y = e-x [(C₁ + C₂x) cos x + (C₃+ C₄x) sin x]

 

Example 5.1.9 (b) If 1 ± 2i, 1 ± 2i are the roots of the auxiliary equation corresponding to a fourth order homogeneous linear differential equation F (D) y = 0, find its solution. [A.U M/J 2016 R-13]

Solution :

Given: m = 1 ± 2i [twice]

y = ex [(C₁+ 2x) cos 2x + (C₃ + C₄x) sin 2x]

 

Example 5.1.9 (c) Solve (D⁴ + 1) y = 0

 [A.U N/D 2016 R-8]

Solution: Given: (D⁴ + 1) y = 0

The auxiliary equation is m⁴ + 1 = 0 ⇒ m⁴  = −1 = e^iπ

 

Example 5.1.9 (d) Solve (D⁴ - 2D² + 1) y = 0[A.U. N/D 2019, R-17]

Solution: Given:

(D⁴ - 2D² + 1) y = 0

⇒ (D² -1)²  y = 0

The auxiliary equation is (m² - 1)² = 0

⇒ m² - 1 = 0 ⇒ m² = 1 ⇒ m = ±1

m = 1, 1, -1, -1

y = e^x (C₁x + C₂) + e^-x (C₃x + C₄)