Probability and complex function: Unit V: Ordinary Differential Equations
(b) problems based on legendre's linear differential equation
Solved Example Problems | Ordinary Differential Equations
where k's are constants and Q is a function of x is called Legendre's linear differential equations. Such equations can be reduced to linear equations with constant coefficients by putting
III. (b) PROBLEMS
BASED ON LEGENDRE'S LINEAR DIFFERENTIAL EQUATION
(EQUATION REDUCIBLE
TO LINEAR FORM)
An
equation of the form
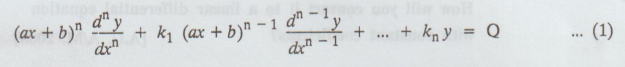
where
k's are constants and Q is a function of x is called Legendre's linear
differential equations. Such equations can be reduced to linear equations with
constant coefficients by putting
ax
+ b = ez
(i.e.,) z = log (ax + b )
If
D' = d/dz , then (ax + b)D = aD'
(ax+b)2 D2 = a2
D' (D' - 1) and so on.
After
making these substitutions in (1), it reduces to a linear differential equation
with constant coefficients.
Legendre's
linear differential equation can be reduced to the Euler homogeneous linear
forms also, by putting ax + b = t and then solved by the Euler's method.
Example 5.3.24. Solve (x + 2)2d2y/dx2
– (x+2)dy/dx + y = 3x + 4 [A.U.
Nov. 2001] [A.U A/M 2019 R-17] [A.U. N/D 2019, R-17]
Solution: Given:
[(x+2)2 D2 - (x + 2) D + 1]y =3x + 4 .....(1)
Put
x + 2 = ez ⇒
x = ez - 2
log
(x+2)= z
(x+2)
D = D'
(x
+ 2)2 D2 = D' (D' - 1)
[D'
(D' — 1) — D' + 1]y = 3 (ez - 2) + 4
[D'2-D'
- D' + 1]y = 3ez -6 + 4
[D'2
- 2D' + 1]y = 3ez - 2
The
auxiliary equation is m2 - 2m + 1 = 0
(m
− 1)2 = 0 ⇒
m = 1, 1
C.F
= (Az + B) ez =[A log (x + 2) + B] (x + 2)
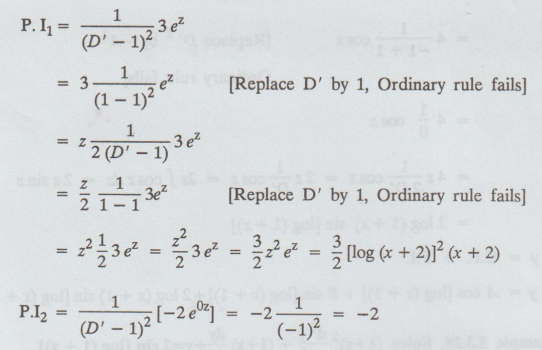
y
= C.F+ P. I1 + P. I2
y
= [A log (x + 2) + B] (x + 2) + 3/2 [log (x + 2)]2 (x + 2) − 2
Example 5.3.25. Solve [(x + 1)2
D2 + (x + 1) D + 1] y = 4 cos [log (x + 1)][A.U. Nov. 2001] [A.U N/D
2011 R-8] [A.U Jan. 2018 R-17]
Solution:
Given: [(x + 1)2 D2 + (x + 1) D + 1]y = 4 cos [log (x +
1)]
Put
1 + x =ez
z
= log (1 + x)
(x+1)D
= D'
(x
+ 1)2 D2 = D' (D' -1)
[D' (D' + D' + 1]y = 4 [cos z]
[D'2
- D' + D' + 1]y = 4 cos z
[D'2 + 1]y = 4 cos z
The
auxiliary equation is m2 + 1 = 0
m
= ± i
C.F.
= [A cos z + B sin z]
=
A cos [log (x + 1)] + B sin [log (x + 1)]
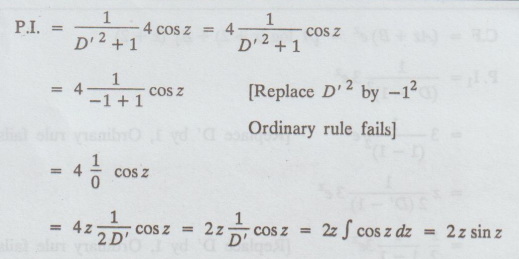
=
2 log (1 + x) sin [log (1 + x)]
y
= C.F. + P.I.
y
= A cos [log (x + 1)] + B sin [log (x + 1)] + 2 log (x + 1) sin [log (x + 1)]
Example 5.3.26. Solve (1+x)2
d2y/dx2 + (1 + x)dy/dx + y = 2 sin [log (1 + x)] [A.U A/M 2011 R-8, A/M 2017 R-13]
Solution: Given:
[(1 + x)2 D2 + (1+x) D + 1]y = 2 sin [ log (1 + x)
Put
1+ x= ez
z
= log (1 + x)
(x
+ 1) D = D'
(x+1)2
D2 = D' (D' - 1)
[D'
(D' - 1) + D' + 1]y = 2 sin z
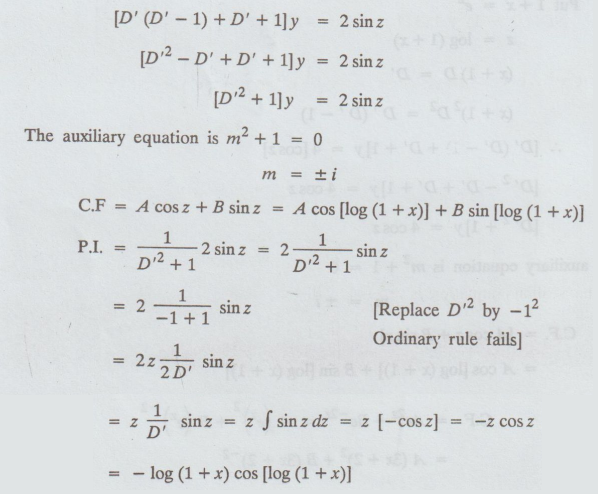
y
= C.F + P.I
y
= A cos [log (1+x)] + B sin [log (1 + x)] - log (1+ x) cos [log (1+x)]
Example 5.3.27. Solve (3x+2)2
D2 + 3 (3x + 2)D - 36 = 3x2 + 4x + 1 [A.U M/J 2013 R-8]
Solution:
Given: [(3x+2)2 D2 + 3 (3x+2) D - 36] y = 3x2
+ 4x + 1
Put
3x + 2 = ez
log
(3x + 2) = Z
3x
= ez – 2
x
=1/3ez – 2/3
Let

Example 5.3.28. Solve (2x+3)2
d2y/dx2 - (2x+3)dy/dx - 12y = 6x [A.U N/D 2002, Jan.
2005]
Solution:
Given: (2x+3)2 d2y/dx2 - (2x+3)dy/dx - 12y =
6x
i.e.,
[(2x+3)2 D2 - (2x + 3) D - 12]y = 6x
Put
2x + 3 = ez
log
(2x+3)= Z
2x
= ez - 3
x
= ez/2 – 3/2
Let
(2x+3) D = 2D'
(2x+3)2 D2 = 22
D' (D'-1) = 4D' (D'-1))

Example 5.3.29 TrAnsform the
equation (2x+3)2 d2y/dx2 - 2(2x+3)dy/dx - 12 y = 6x into
a linear differential equation with constant coefficients. [A.U M/J 2012] [A.U
A/M 2015 R-13]
Solution :
Given: (2x+3)2 d2y/dx2 - 2(2x+3)dy/dx - 12 y = 6x dx2
i.e.,
[(2x+3)2 D2 - 2 (2x+3) D - 12] y = 6x ....(1)
Put
2x + 3 = ez
log
(2x+3)= z
2x
= ez – 3 , x = ez/2
– 3/2
Let
(2x+3)
D = 2 D'
(2x+3)2
D2 = 22 D' (D' - 1) = 4D' (D' -1)
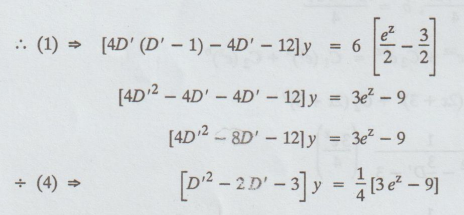
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (b) problems based on legendre's linear differential equation
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
