Probability and complex function: Unit V: Ordinary Differential Equations

(c) Problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2

Solved Example Problems | Ordinary Differential Equations

Home | All Subjects | EEE Department | Probability and complex function
Next >>

Probability and complex function: Unit V: Differential equations : problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2 : Example

I. (c) problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax

⇒ Replace D2 by -a2

 

Example 5.1.20. Find the P.f. of (D2 + 4) y = cos 2x

[AU, May 2001]

Solution: Given: (D2 + 4) y = cos 2x


 

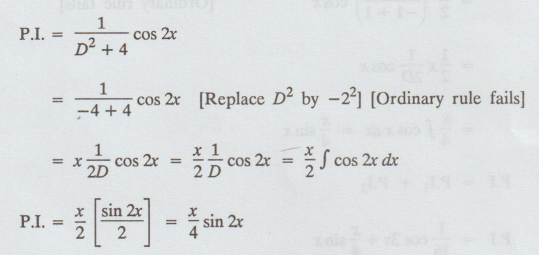
Example 5.1.21. Find the P.I. of (D2 + 1) y = sin x

Solution: Given: (D2 + 1)y = sin x


 

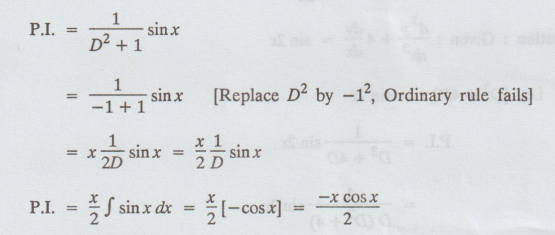
Example 5.1.22. Find the particular integral of (D2 + 1) y = sin x sin 2x

Solution: Given: (D2 + 1) y = sin 2x sin x



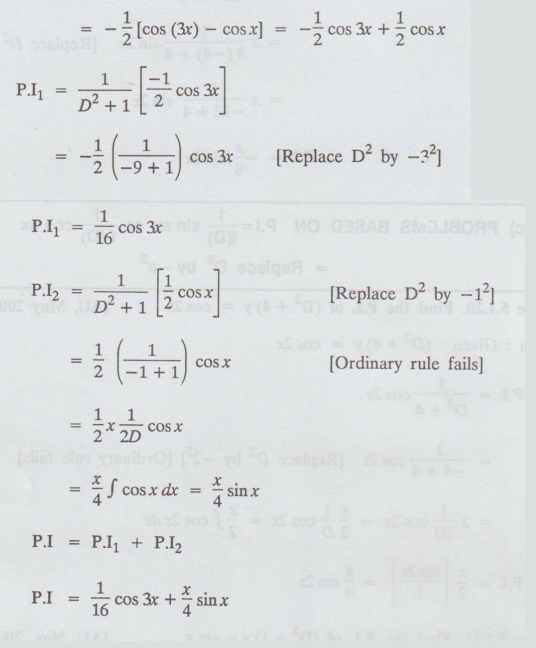
Example 5.1.23. Find the P.I. of d3y / dx3 + 4 dy/dx = sin 2x

Solution: Given: d3y / dx3 + 4 dy/dx = sin 2x

i.e., [D3 + 4D]y = sin 2x


 

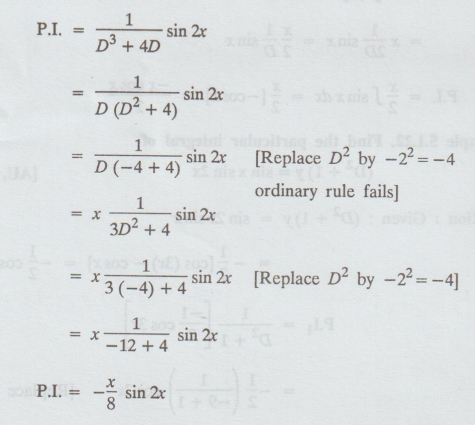
Example 5.1.24. Solve d2y / dx2 + 3 dy/dx + 2y = sin 3x.

Solution :


 

Example 5.1.25. Find the P.I. of (D3 + 1) y = cos (2x − 1)

Solution :


 

Example 5.1.26. Solve (D2 + a2)2 y = sin ax

Solution: Given: (D2+ a2) 2y= sin ax

The auxiliary equation is (m2 + a2)2 = 0


 

Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (c) Problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2

Home | All Subjects | EEE Department | UNIT: Probability and complex function
Next >>

Related Topics


Ordinary Differential Equations - Introduction

Higher order linear differential equations with constant coefficients

(a) Problems based on r.h.s. of the given differential equation is zero - Solved Example Problems | Ordinary Differential Equations

(b) Problems based on P.I.= 1/f(D) eax ⇒ Replace D by a - Solved Example Problems | Ordinary Differential Equations

(c) Problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2 - Solved Example Problems | Ordinary Differential Equations

(d) problems based on R.H.S = eax + sin ax(or) eax + cos ax - Solved Example Problems | Ordinary Differential Equations

(e) problems based on R.H.S = xn - Solved Example Problems | Ordinary Differential Equations

(f) Problems based on R.H.S. = eax X - Solved Example Problems | Ordinary Differential Equations

(g) problems based on f(x) = x V type - Solved Example Problems | Ordinary Differential Equations

(h) problems based on eax integral e-ax - Solved Example Problems | Ordinary Differential Equations

(i) General ode problems - Solved Example Problems | Ordinary Differential Equations

(i) Problems based on R.H.S = eax + xn + cos ax - Solved Example Problems | Ordinary Differential Equations

Exercise 5.1 (Ordinary Differential Equations) - Problems with Answer

Method of variation of parameters - Ordinary Differential Equations

Problems based on method of variation of parameters - Solved Example Problems | Ordinary Differential Equations

Related Subjects


Probability and complex function

Probability and complex function

MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation