Probability and complex function: Unit V: Ordinary Differential Equations

(e) problems based on R.H.S = xn

Solved Example Problems | Ordinary Differential Equations

Home | All Subjects | EEE Department | Probability and complex function
Next >>

Probability and complex function: Unit V: Differential equations: 1. (e) problems based on R.H.S = xn : Examples

1. (e) PROBLEMS BASED ON  R.H.S = xn

Note: The following formulae are important.

(1 + x)-1 = 1 – x + x2 – x3 + …

(1 + x)-1 = 1 + x + x2 + x3 + …

(1 + x)-2 = 1 – 2x + 3x2 – 4x3 + …

(1 + x)-2 = 1 – 2x + 3x2 + 4x3 + …

 

Example 5.1.30. Solve d2y / dx2 - 5 dy/dx + 6y = x2 + 3.

Solution :

Given : d2y / dx2 - 5 dy/dx + 6y = x2 + 3.

i.e., (D2 - 5D+6) y = x2 + 3

The auxiliary equation is m2 - 5m + 6 = 0

⇒ m = 3, m = 2


 

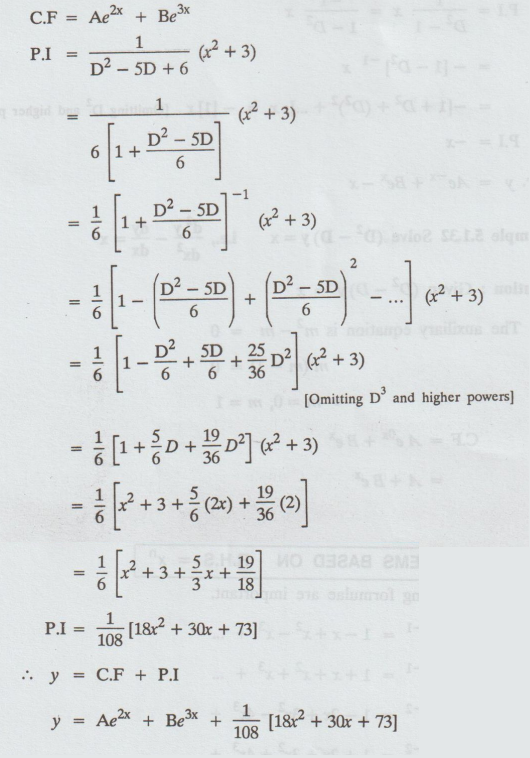
Example 5.1.31 Solve (D2 - D) y = x

Solution:

Given (D2 - D) y = x

The auxiliary equation is m2 – 1 = 0

m2 = 1

m = ± 1


 

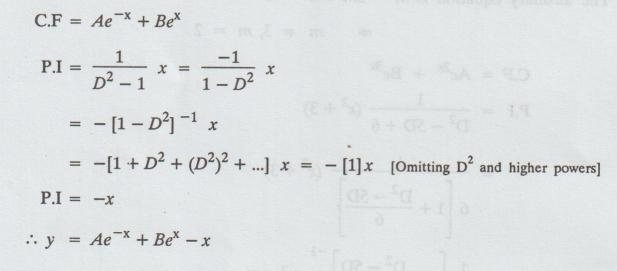
Example 5.1.31 Solve (D2 - D) y = x  i.e, d2y / dx2 – dy / dx = x

Solution:

Given (D2 - D) y = x

The auxiliary equation is m2 – m = 0

m(m – 1) = 0

⇒ m = 0, m = 1


 

Example 5.1.33. Solve (D3 - 3D2 - 6D+8) y = x

Solution: Given: (D3 - 3D2 - 6D+8) y = x

The auxiliary equation is (m3 - 3m2 - 6m+8) = 0

⇒ m = 1, m = -2, m = 4


 

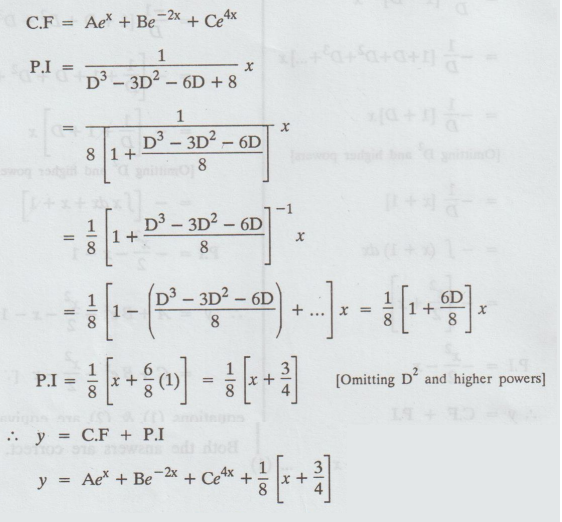
Example 5.1.34. Solve [D4 - 2D3 + D2] y = x3.

Solution:

 Given: [D4 - 2D3 + D2] y = x3

The auxiliary equation is m4 - 2m3 + m2 = 0

m2 (m2 - 2m + 1) = 0

m2 (m - 2m + 1) = 0

m2 (m-1)2 = 0

m = 0, 0, m = 1, 1


 

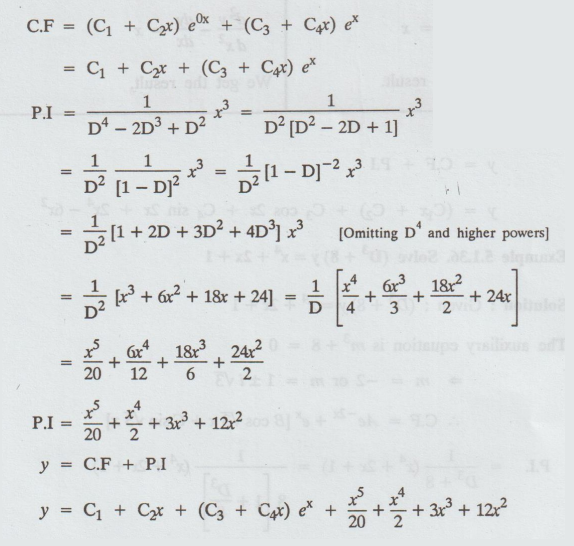
Example 5.1.35. Solve D2 (D2 + 4) y = 96x2

Solution: Given: D2 (D2 + 4) y = 96x2

The auxiliary equation is m2 (m2 + 4) = 0

m2 = 0, m2 + 4 = 0,

m = 0, 0 m = ± 2i


 

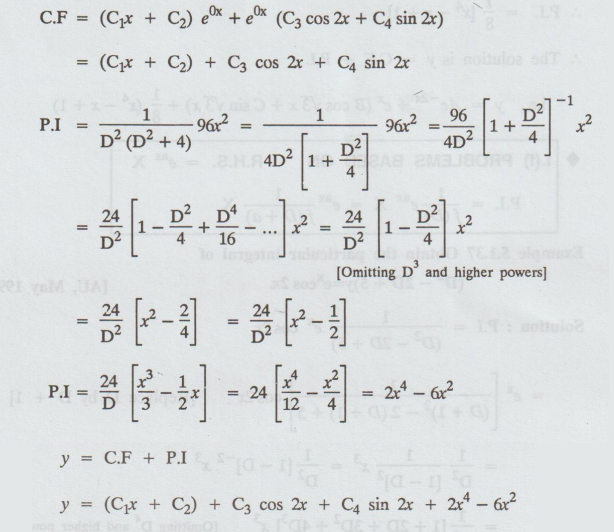
Example 5.1.36. Solve (D3 +8) y = x4 + 2x + 1

Solution: Given: (D3 +8) y = x4 + 2x + 1

The auxiliary equation is m3 + 8 = 0


 

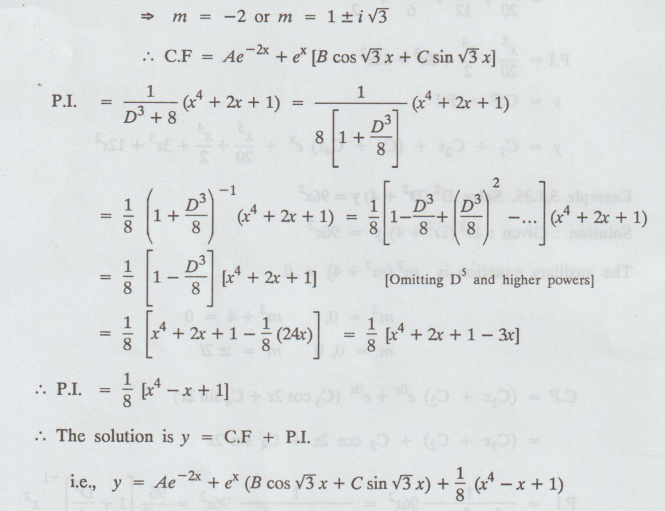
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (e) problems based on R.H.S = xn

Home | All Subjects | EEE Department | UNIT: Probability and complex function
Next >>

Related Topics


Ordinary Differential Equations - Introduction

Higher order linear differential equations with constant coefficients

(a) Problems based on r.h.s. of the given differential equation is zero - Solved Example Problems | Ordinary Differential Equations

(b) Problems based on P.I.= 1/f(D) eax ⇒ Replace D by a - Solved Example Problems | Ordinary Differential Equations

(c) Problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2 - Solved Example Problems | Ordinary Differential Equations

(d) problems based on R.H.S = eax + sin ax(or) eax + cos ax - Solved Example Problems | Ordinary Differential Equations

(e) problems based on R.H.S = xn - Solved Example Problems | Ordinary Differential Equations

(f) Problems based on R.H.S. = eax X - Solved Example Problems | Ordinary Differential Equations

(g) problems based on f(x) = x V type - Solved Example Problems | Ordinary Differential Equations

(h) problems based on eax integral e-ax - Solved Example Problems | Ordinary Differential Equations

(i) General ode problems - Solved Example Problems | Ordinary Differential Equations

(i) Problems based on R.H.S = eax + xn + cos ax - Solved Example Problems | Ordinary Differential Equations

Exercise 5.1 (Ordinary Differential Equations) - Problems with Answer

Method of variation of parameters - Ordinary Differential Equations

Problems based on method of variation of parameters - Solved Example Problems | Ordinary Differential Equations

Related Subjects


Probability and complex function

Probability and complex function

MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation