(g) problems based on f(x) = x V type

I(g) PROBLEMS BASED ON f(x) = x V TYPE

To find P.I, when f(x) = x V

1 / f(D) xV = x 1 / f(D) V – f(D) / [f(D)]² V

where V is any function of x and f' (D) is the derivative of f (D) w.r.to D.

Example 5.1.45(a) Find the particular integral of (D² - 4D) y = e^x x

[A.U N/D 2015 R-13]

Solution :

Example 5.1.45(b). Solve (D² + 4D + 3) y = e ^–x sin x + xe^3x.

Solution :

Given: (D² + 4D + 3) y = e ^–x sin x + xe^3x

The auxiliary equation is m² + 4m + 3 = 0

⇒ m = -1, m= = -3

C.F = Ae^-x + Be^-3x

Example 5.1.46 Solve: (D³ - 7D - 6) y = (1 + x) e^2x)

 [A.U N/D 2014]

Solution :

Given: (D³ - 7D - 6) y = (1 + x) e^2x)

The auxiliary equation is m³ - 7m - 6 = 0

Example 5.1.47. Solve (D³ - D) y = e^x x.

Solution:

Given: (D³ - D) y = e^x x.

The auxiliary equation is m³ – m = 0

m (m² − 1) = 0

m = 0, m² = 1

m = ± 1

Note: P.I = (1 / D³ – D) xe^x, we should not be applied x V type as calculation

of (1 / D³ – D)e^x  will come under the cases of failure. 

Example 5.1.48. Solve (D² + 4) y = x sin x

Solution: Given: (D² + 4) y = x sin x

The auxiliary equation is m² + 4 = 0

m = ± 2i

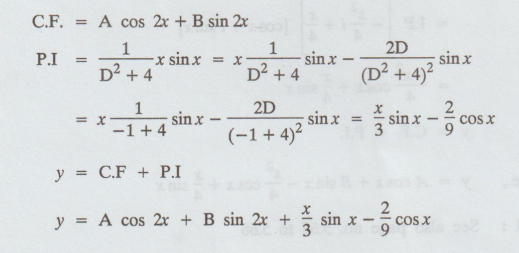
Example 5.1.49 Solve (D² + 1) y = x sin x

Solution: Given: (D² + 1)y = x sin x

The auxiliary equation is m² + 1 = 0; m = ±i

C.F= A cos x + B sin x

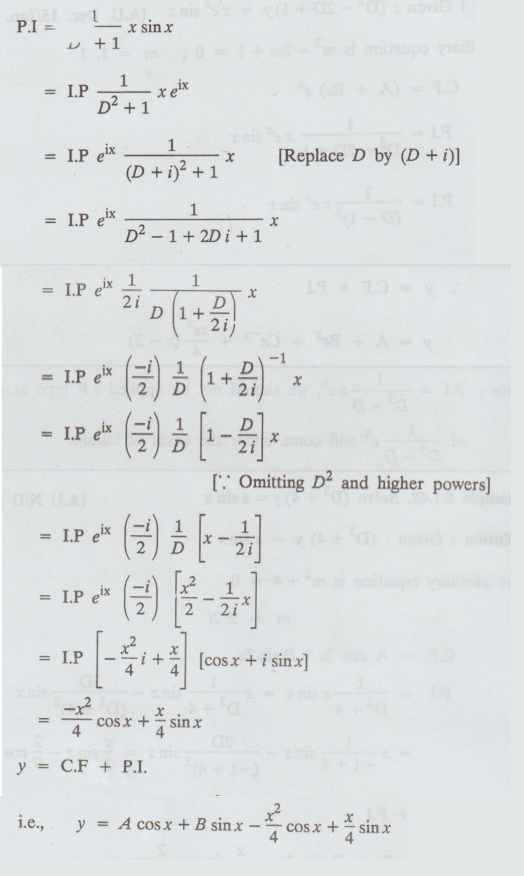
Note 1 : Had the question been (D² + 1) y = x sinx, then the above (XV) method should not be applied as calculation of 1 / D² + 1 sin x will come under the cases of failure.

Example 5.1.50. Solve (D² - 2D + 1) y = xe^x sin x

[A.U N/D 2013] [A.U. Dec. 15/Jan. 16 R-8]

Solution: Given: (D² - 2D + 1)y = xe^x sin x

The auxiliary equation is m² - 2m + 1 = 0; m = 1, 1

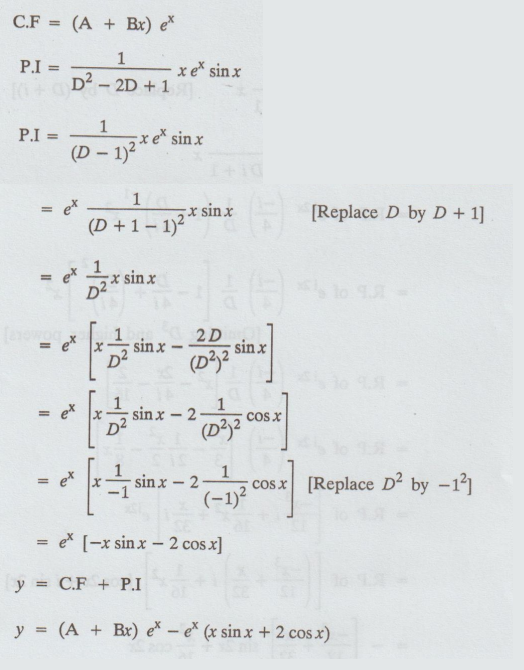
Example 5.1.51. Solve the equation (D² + 4) y = x² cos 2x. [A.U M/J 2009]

Solution: The auxiliary equation is m² + 4 = 0

The roots are m = ± i2

C.F = A cos 2x + B sin 2x

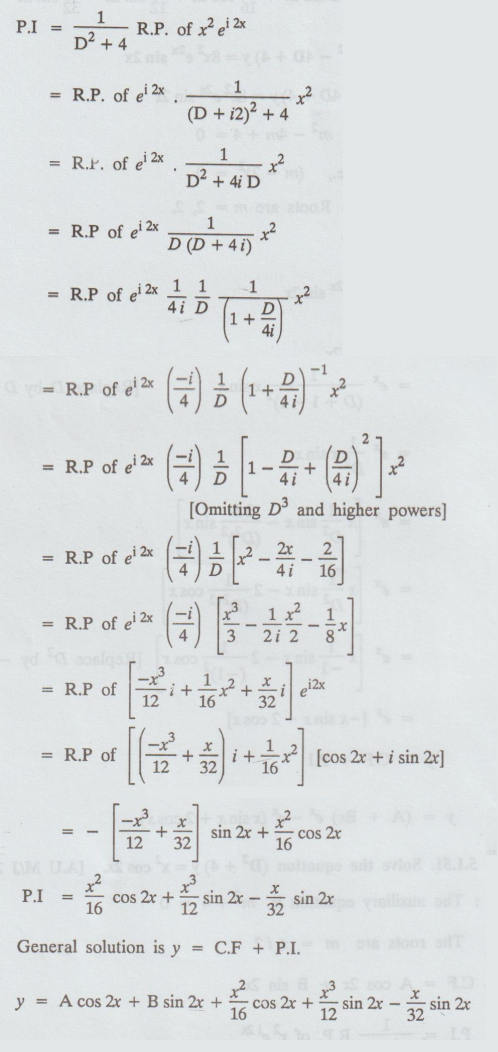
Example 5.1.52. Solve (D² - 4D + 4) y = 8x² e^2x sin 2x

Solution: Given: (D² - 4D + 4) y = 8x² e^2x sin 2x

The auxiliary equation is m² - 4m + 4 = 0

i.e., (m - 2)² = 0

Roots are m = 2, 2.

Example 5.1.53. Solve (D³ - 1) y = x sin x.

Solution: Given: (D³ - 1) y = x sinx

The auxiliary equation is m³ - 1 = 0

i.e., (m − 1) (m² + m + 1) = 0