Probability and complex function: Unit V: Ordinary Differential Equations

(i) General ode problems

Solved Example Problems | Ordinary Differential Equations

Home | All Subjects | EEE Department | Probability and complex function
Next >>

Probability and complex function: Unit V: Differential equations : general ode problems

 (i) GENERAL ODE PROBLEMS

 

Example 5.1.55. Solve d2y/dx2 – 6 dy/dx + 9y = 6e3x + 7e-2x – log 2

Solution:

Given: (D2 - 6D + 9) y = 6e3x + 7e-2x – log 2 e0x

The auxiliary equation is m2 - 6m + 9 = 0

 (m − 3)2 = 0

m = 3, 3

C.F = (C1 + C2x)e3x


 

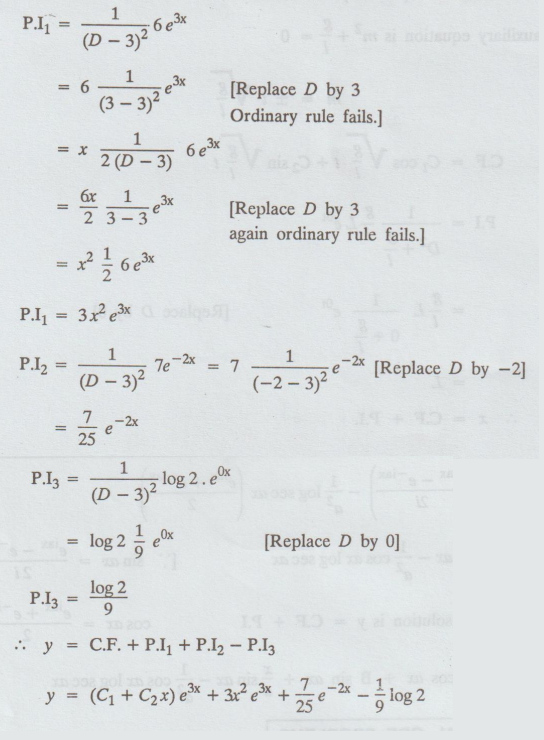
Example 5.1.56. Solve the differential equation d2x / dt2 + g/l x = g/l L

where g, l, L are constants subject to the conditions,

x = a, dx/dt = 0 at t = 0.

[Note: This is an I.V.P.]

Solution:


 

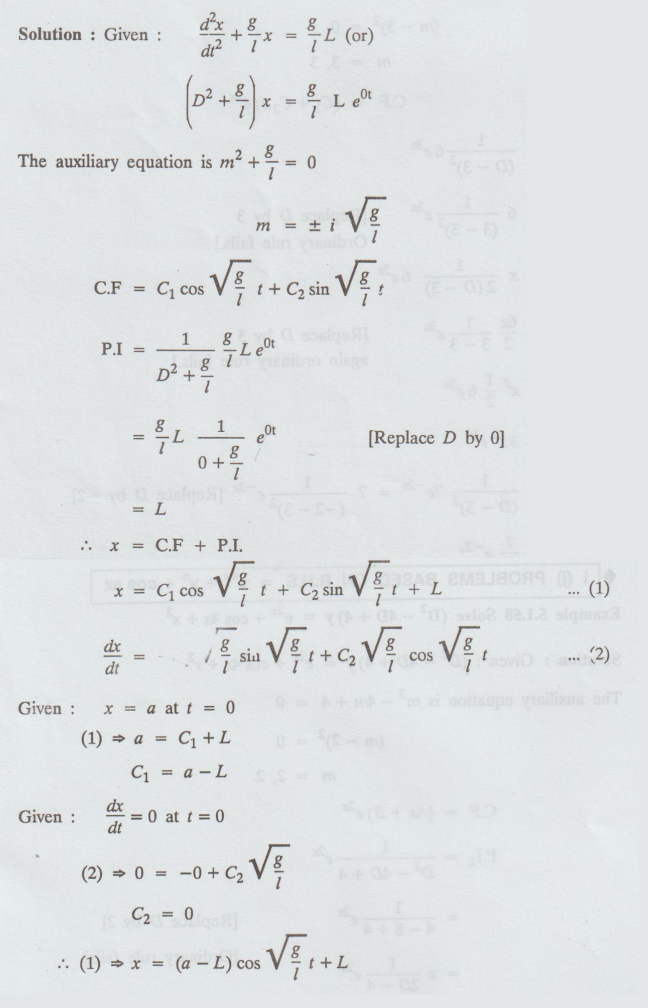
Example 5.1.57. Solve (D2 - 6D + 13) y = 2x

Solution: Given: (D2 - 6D +13) y = 2x

i.e., (D2 - 6D +13) y = e(log 2x) = ex log 2

(D2 - 6D +13) y = e(log 2x)

The auxiliary equation is m2 – 6m + 13 = 0


 

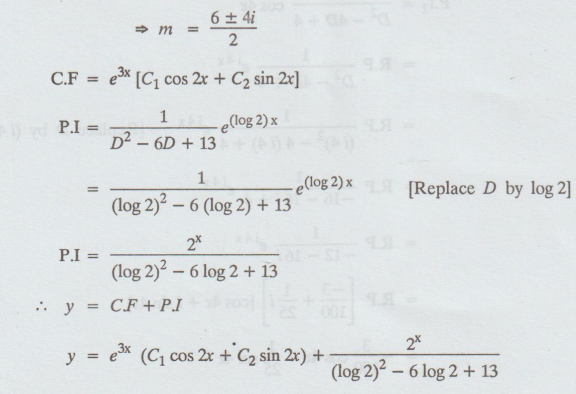
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (i) General ode problems

Home | All Subjects | EEE Department | UNIT: Probability and complex function
Next >>

Related Topics


Ordinary Differential Equations - Introduction

Higher order linear differential equations with constant coefficients

(a) Problems based on r.h.s. of the given differential equation is zero - Solved Example Problems | Ordinary Differential Equations

(b) Problems based on P.I.= 1/f(D) eax ⇒ Replace D by a - Solved Example Problems | Ordinary Differential Equations

(c) Problems based on P.I = 1 / f(D) sin ax or 1 / f(D) cos ax ⇒ Replace D2 by -a2 - Solved Example Problems | Ordinary Differential Equations

(d) problems based on R.H.S = eax + sin ax(or) eax + cos ax - Solved Example Problems | Ordinary Differential Equations

(e) problems based on R.H.S = xn - Solved Example Problems | Ordinary Differential Equations

(f) Problems based on R.H.S. = eax X - Solved Example Problems | Ordinary Differential Equations

(g) problems based on f(x) = x V type - Solved Example Problems | Ordinary Differential Equations

(h) problems based on eax integral e-ax - Solved Example Problems | Ordinary Differential Equations

(i) General ode problems - Solved Example Problems | Ordinary Differential Equations

(i) Problems based on R.H.S = eax + xn + cos ax - Solved Example Problems | Ordinary Differential Equations

Exercise 5.1 (Ordinary Differential Equations) - Problems with Answer

Method of variation of parameters - Ordinary Differential Equations

Problems based on method of variation of parameters - Solved Example Problems | Ordinary Differential Equations

Related Subjects


Probability and complex function

Probability and complex function

MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation