Probability and complex function: Unit V: Ordinary Differential Equations
(i) Problems based on R.H.S = eax + xn + cos ax
Solved Example Problems | Ordinary Differential Equations
Probability and complex function: Unit V: Differential equations : Examples
I (i) problems based on R.H.S = eax + xn +
cos ax
Example
5.1.58 Solve (D2 - 4D + 4) y = e2x + cos 4x + x2
Solution:
Given: (D2 - 4D + 4) y = e2x + cos 4x + x2
The
auxiliary equation is m2 – 4m + 4 = 0
(m − 2)2 = 0
m
= 2, 2
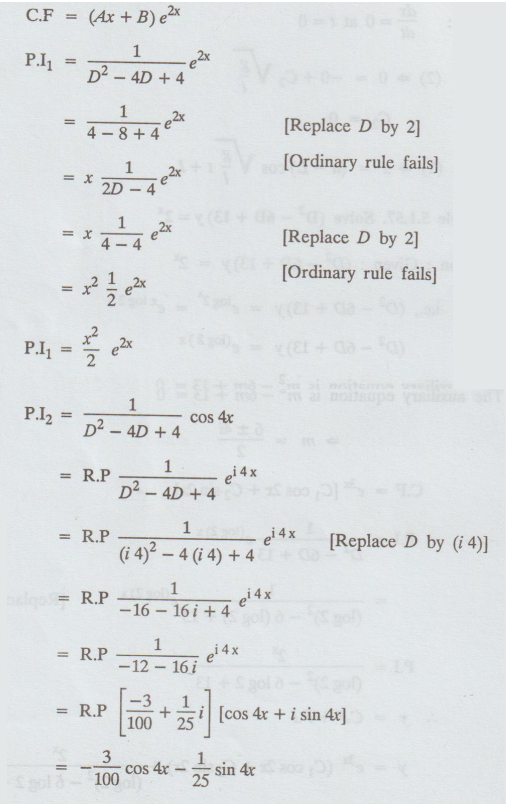
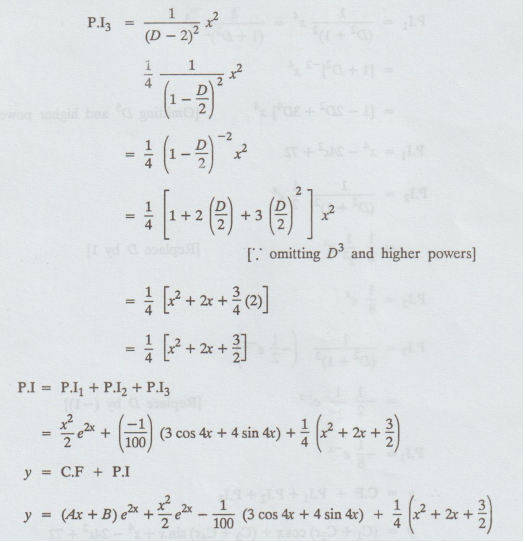
Example 5.1.59 Solve (D2+1)2
= x4 + sinh x
Solution:
Given. (D2 + I)2 = x4 + [ ex – e-x /2 ]
((D2
+ 1)2 = x4 + 1/2 ex
– 1/2 e-x
The
auxiliary equation is (m2 + 1)2 = 0
m2
+ 1 = 0, m2 + 1 = 0
m2
= -1, m2 = -1
m
= ± i, m2 = ± i
C.F
= C1+C2) cosx + (C3 + C4x) sinx
P.I1
=1/(D2 + 1)2 x4= [1/(1+ D2)2
x4
=
[1
+ D2]-2 x4
=
[1 - 2D2 + 3D4] x4
[Omitting D5 and higher powers]
P.I1
= x4 - 24x2 + 72
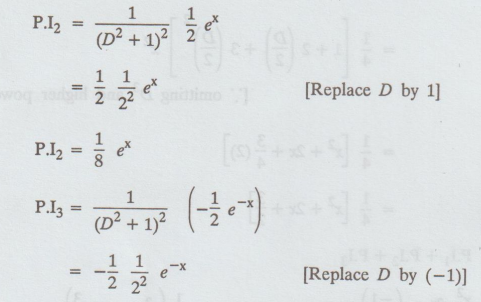
P.I3
= -1/8 ex
y
= C.F + P.I1 + P.I2+ P.I3
y
= (C1 + C2x) cosx + (C3 + C4x) sinx
+ x4 – 24x2 + 72 + 1/8 ex – 1/8 e-x
Example 5.1.60 Solve: (D4+
D3 + D2) y = 12x2 + 2 cos 2x cosx
Solution:
Given: (D4 + D3 + D2) y = 12x2 +
[cos (2 + 1)x + cos (2-1) x]
i.e.,
[D4 + D3 + D2ly = 12x2 + cos 3x +
cos x
The
auxiliary equation is m4 + m3 + m2 = 0
m2
[m2 + m + 1] = 0
m2
= 0 , m2 + m + 1 = 0
m
= 0, 0 and m = -1/2 ± √3i/2
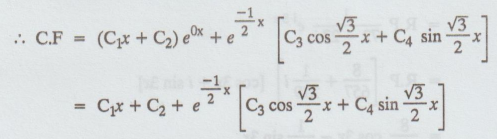
P.I1
= 1/D4 + D3 + D2 12 x2
=
12/D2 1/ 1 + D+D2 ]x2
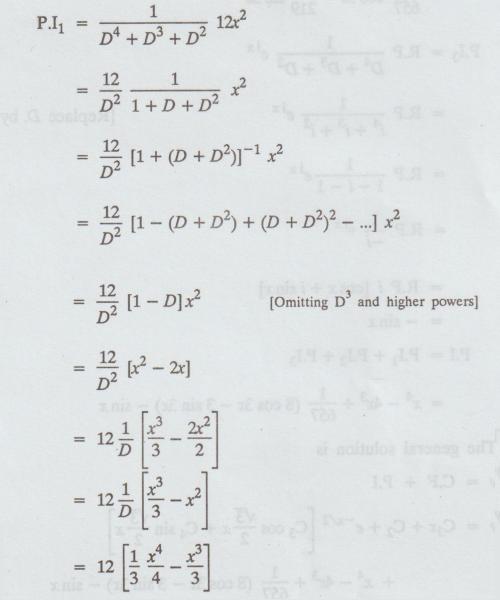
P.I1
= x4 - 4x3
P.I2 = 1/D4 + D3 + D2
cos 3x
P.I2 =R.P. 1/D4 + D3 +
D2 ei3x [Replace D
by (i 3)]
=
R.P 1/(i 3)4 + (i 3)3 + (i 3)2 ei3x
= RP 1/81 -27i – 9 ei3x
=
R.P 1/72 - 27i ei3x
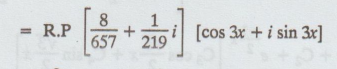
=
8/657 cos 3x – 1/219 sin 3x
P.I3
= R.P 1/ D4 + D3 + D2 eix
= R.P 1/i4 +i3 + i2
eix [Replace D by i]
=
R.P 1/1 – i – 1 eix
=R.P
1/-i eix
=
R.P i [cos x + i sin x]
=
-sin x
P.I
= P.I1+ P.I2 + P.I3
=
= x4 - 4x3 + 1/657 (8 cos 3x - 3 sin 3x) - sin x
The
general solution is
y
= C.F + P.I
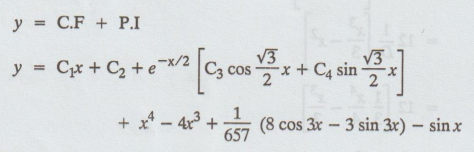
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Solved Example Problems | Ordinary Differential Equations - (i) Problems based on R.H.S = eax + xn + cos ax
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
