3.1 (b) newton's method [or Newton-Raphson method]

3.1 (b) NEWTON'S METHOD [or Newton-Raphson method]

Newton's algorithm is widely used because, in the near neighbourhood of a root, it is more rapidly convergent than any of the methods discussed so far. The method is quadratically convergent, by which we mean that the error of each step approaches a constant k times the square of the error of the previous step. The net result of this is that the number of decimal places of accuracy nearly doubles at each iteration. This method is also based on a linear approximation of the function, but it is useful for tangent to the curve.

Graphical description :

Starting from a single initial estimate, xo, that is not too far from a root, we move along the tangent to its intersection with the x axis, and take that as the next approximation. This is continued until either the successive x-values are sufficiently close or the value of the function is sufficiently near zero.

The angle of inclination of the tangent line to the curve at x = xo as one of its acute angles.

Pitfalls of Newton-Raphson method

Although the Newton-Raphson method is often very efficient, there are situations where it performs poorly.

Example :

Thus, after the first poor prediction, the technique is converging on the true root of 1, but at a very slow rate.

There is no general convergence criterion for Newton-Raphson. Its convergence depends on the nature of the function and on the accuracy of the initial guess. The only way is to have an initial guess that is "sufficiently" close to the root.

Note: 1. The error at any stage is proportional to the square of the error in the previous stage.

2. The method is also called method of tangents.

3. The order of convergence of the Newton-Raphson method is atleast 2 or the convergence of N-R. method is quadratic.

Newton's method fails, if f(x₀) / f'(x₀) is not small enough. This happens if the graph of the function y = f (x) near the root is rather flat. Sometimes though the curve is not rather flat but a wrong choice of initial approximation may lead to the failure of the Newton's method.

Another case of failure is the situation where two roots of the equation are close together.

Comparison of Newton's method with the Regula-Falsi method

Regula-Falsi is surely convergent while Newton's method is conditionally convergent. On the other hand, once the Newton's method converges, it converges faster. In Regula falsi method, we calculate only one more value of function at each step, while in Newton's method, we require two calculations at each step.

Therefore, Newton's method generally requires less number of iterations while Regula-Falsi method requires more time for computations at each iteration.

Criterion for convergence

Sufficient condition :

1. Find the positive root of x⁴ - x = 10 correct to three decimal places using Newton-Raphson method.  [AU May 1996, AU A/M 2010]

Solution :

Here , x2 = x3 = 1.856

Hence, the better approximate root is 1.856.

2. Using Newton's iterative method, find the root between 0 and 1 of x³ = 6x - 4 correct to two decimal places. [A.U May 2000] [A.U M/J 2008, AU M/J 2012, A.U A/M 2017 R-08]

Solution :

Note: Fix 2 decimal places in your calculator.

Here, x₂ = x₃ = 0.73

3. Find the real positive root of 3x cos x - 1 = 0 by Newton's method correct to 6 decimal places. [A.U A/M 2007, 2019 (R-17) (R-13), 2017 (R-13), 2016, 2021 (R-17)] [A.U N/D 2009, 2014, 2020 (R-17), 2021 (R-17)]

Solution :

Note: (1) Fix 6 decimal places in your calculator.

 (2) Change degree mode to radian mode in your calculator.

4. Find by N-R method, the root of log10 x = 1.2.  [M.U. Oct., 1995] [A.U N/D 2016 R-13]

Solution :

Note : Fix 4 decimal places in your calculator.

5. Find the root of cos x = x e^x by Newton-Raphson method.  [M.U. April, 1996]

Solution :

Note :

(1) Fix 4 decimal places in your calculator.

(2) Change degree mode to radian mode in your calculator.

Hence, the better approximate root is 0.5178.

6. Find to 4 decimals by Newton's method, a root x^sin2 – 4 = 0

Solution :

Note : (1) Fix 4 decimal places in your calculator.

(2) Change degree mode to radian mode in your calculator.

7. Solve by Newton's method, a root of e^x - 4x = 0. [M.U. April, 1997]

Solution :

Note: Fix 4 decimal places in your calculator.

Hence, the better approximate root is 0.3574.

8. Find a root of x log10x - 1.2 = 0 by N.R method correct to three

decimal places. [A.U. Nov./Dec 2004] [A.U M/J 2007] [A.U CBT M/J 2010, Tvli M/J 2010, CBT N/D 2010] [A.U A/M 2015 (R8-10)] [A.U N/D 2016 R-13]

Solution :

Note : Fix 4 decimal places in your calculator.

Here, x₂ = x₃ = 2.741.

[Hence, the better approximation is 2.741

9. Evaluate √15 using Newton-Raphson's formula. [A.U A/M. 2014]

Solution :

Here, x₀ = X₁ = 3.873

Hence, the better approximate root is 3.873

10. Using N-R method, solve x log₁₀ x = 12.34 start with x₀ = 10. [Anna, A/M 2004]

Solution :

Note: Fix 3 decimal places in your calculator.

Here, x₂ = x₃ = 11.595.

Hence, the better approximate root is 11.595.

11. Write down Newton-Raphson formula for finding √a where a is a positive number and hence find √5.

Solution:

Here, x₂ = x₃ = 2.2361

Hence, the approximate value of √5 = 2.2361

[Correct to four decimal places]

12. Obtain Newton's iterative formula for finding √N where N is a positive real number. Hence evaluate. √142. [Anna, May 1999]

Solution: We know that, the iterative formula for √N is

Here, x₂ = x₃ = 11.9164

Hence, the value of √142 = 11.9164

[correct to four decimal places]

Generalised Newton's method

If a is a root of f (x) = 0 with multiplicity K, then the iteration formula will be

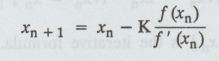
It means that 1 / K f'(x) is the slope of the line through (x_n, y_n) and intersecting the axis of x at (x_n+1, 0).

Since, a is a root of f (x) = 0 with multiplicity K, it implies that K is also a root of f'(x) = 0 with multiplicity (K-1) and it is a root of O with multiplicity (K-2) and so on.

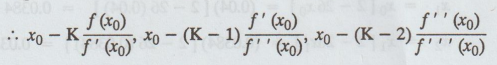
will have the same value, if the initial approximation xo is chosen close to the actual root.

13. Find the iterative formula for finding the value of 1 / N where N is a  real number, using Newton-Raphson method. Hence evaluate 1 / 26 correct to 4 decimal places. [Anna, Nov. 1996] [A.U CBT A/M 2011] [A.U. N/D 2012] [A.U M/J 2013]

Solution :

Hence, the value of 1/26 = 0.0385 [correct to four decimal places]

14. Find the double root of x³-x²-x+1 = 0 choosing x₀ = 0.8.

Solution:

Hence, the approximate root is 1