A General Form of LC Oscillator Circuit

A General Form of LC Oscillator Circuit

• It uses BJT, FET or op-amp in its amplifier stage, with gain of amplifier stage as Av.

• The feedback network uses three impedances Z v Z2 and Z3.

• An amplifier stage provides 180° phase shift while the feedback network contributes additional 180° phase shift to satisfy Barkhausen condition.

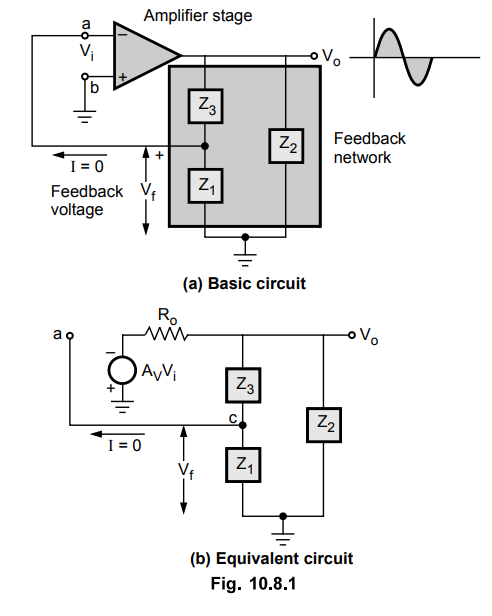
• The Fig. 10.8.1 (a) shows the basic form of LC oscillator while the Fig. 10.8.1 0?) shows the equivalent circuit assuming infinite input impedance of an amplifier stage.

Analysis of amplifier stage :

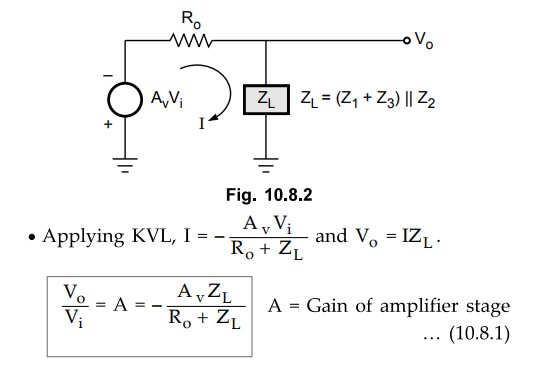
• Let R_o be the output impedance of the amplifier stage.

• As I = 0 due to infinite input impedance, Z₁ and Z₃ appear in series and the combination in parallel with Z₂ as shown in the Fig. 10.8.2.

Analysis of feedback stage :

• To calculate β, consider feedback stage as shown in the Fig. 10.8.3.

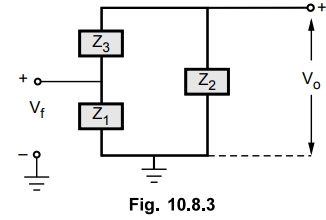
• By voltage division in parallel circuit,

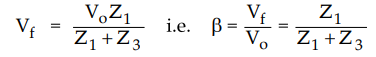
• But as feedback network introduces 180° phase shift, use negative sign.

Expression of the loop gain :

• According to Barkhausen condition loop gain –Aβ is,

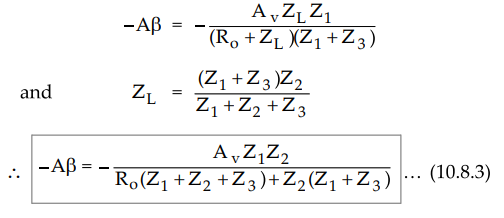
The impedances Z₁ Z₂, Z₃ are pure reactive elements either L or C.

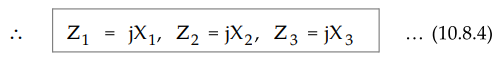
Thus the loop gain becomes,

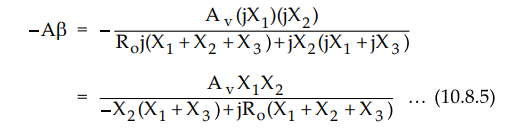
• To have 0° phase shift for the loop gain, the imaginary part must be zero.

• According to Barkhausen condition loop gain  -Aβ must be positive and greater than equal to 1. As A_V is positive, -Aβ will be positive only when X₁ and X₂ have same sign.

• Thus X₁ and X₂  must be of same type, either inductive or capacitive. And as X₁ + X₃ = -X₂ i.e. X₃ = -(X₁ + X₂)  the element X₃ must be opposite type of reactance to X₁ and X₂.

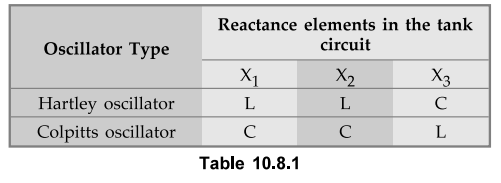
1. Types of LC Oscillators

• In LC oscillators, if X₁ and X₂ are inductive, X₃ must be capacitive and if X₁ and X₂ are capacitive, then X₃ must be inductive. This decides the two types of LC oscillators as,

Review Question

1. Discuss and explain the basic circuit of an LC oscillator and derive the condition for the oscillations.