Adders

Adders

AU : Nov.-l0, May-15, 16

• Digital computers perform various arithmetic operations. The most basic operation, no doubt, is the addition of two binary digits. This simple addition consists of four possible elementary operations, namely,

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10₂

• The first three operations produce a sum whose length is one digit, but when the last operation is performed sum is two digits. The higher significant bit of this result is called a carry and lower significant bit is called sum. The logic circuit which performs this operation is called a half-adder. The circuit which performs addition of three bits (two significant bits and a previous carry) is a full-adder.

1. Half Adder

• The half-adder operation needs two binary inputs : Augend and addend bits; and two binary outputs : stun and carry. The truth table shown in Table 3.11.1 gives the relation between input and output variables for half-adder operation.

Limitations of Half-Adder :

• In multidigit addition we have to add two bits along with the carry of previous digit addition. Effectively such addition requires addition of three bits. This is not possible with half-adder. Hence half-adders are not used in practice.

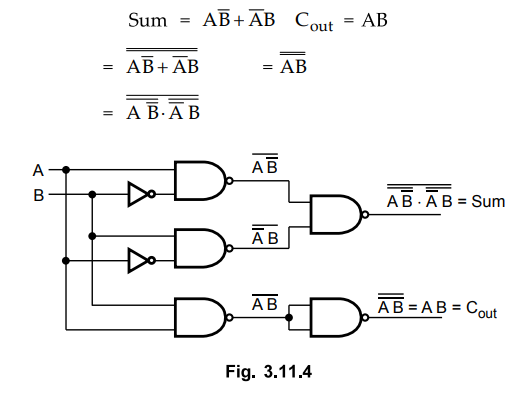
Ex. 3.11.1 Draw half adder using NAND gates.

Sol. : For half adder :

2. Full Adder

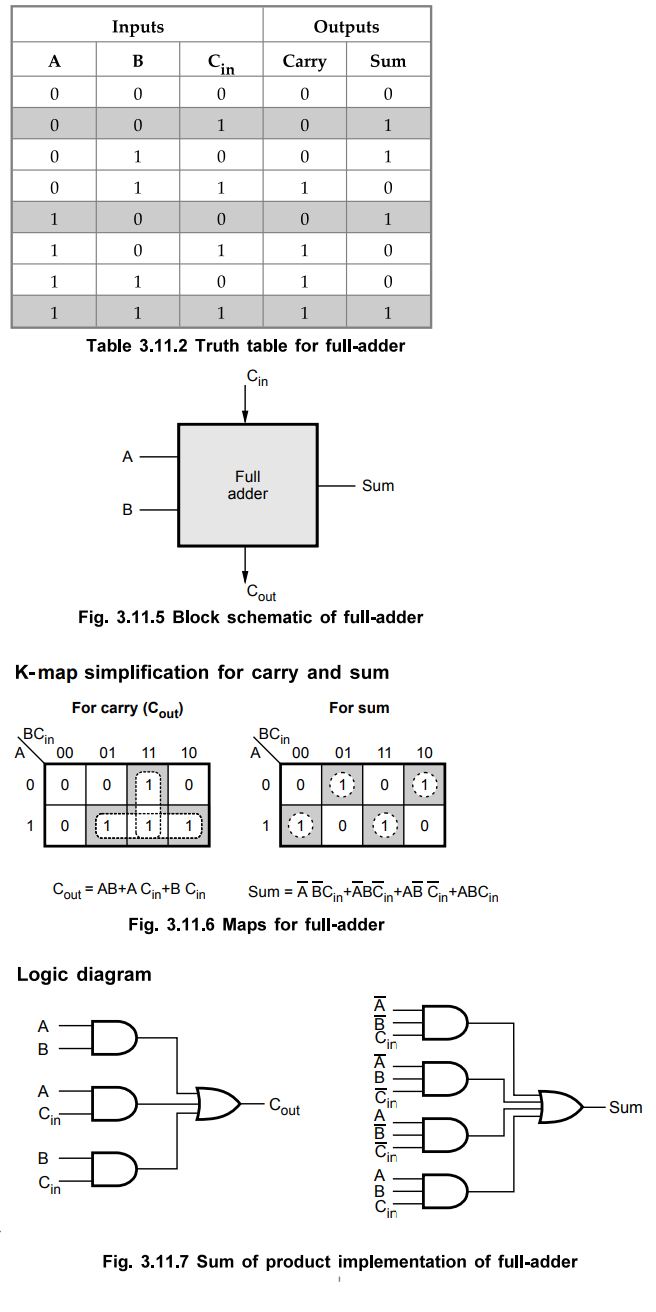
• A full-adder is a combinational circuit that forms the arithmetic sum of three input bits. It consists of three inputs and two outputs. Two of the input variables, denoted by A and B, represent the two significant bits to be added. The third input Cin, represents the carry from the previous lower significant position. The truth table for full-adder is shown in Table 3.11.2.

The Boolean function for sum can be further simplified as follows :

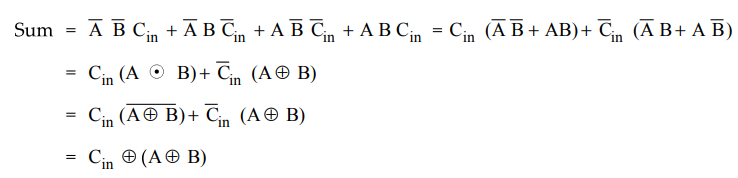
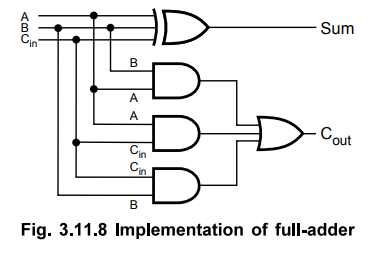
With this simplified Boolean function circuit for full-adder can be implemented as shown in the Fig. 3.11.8.

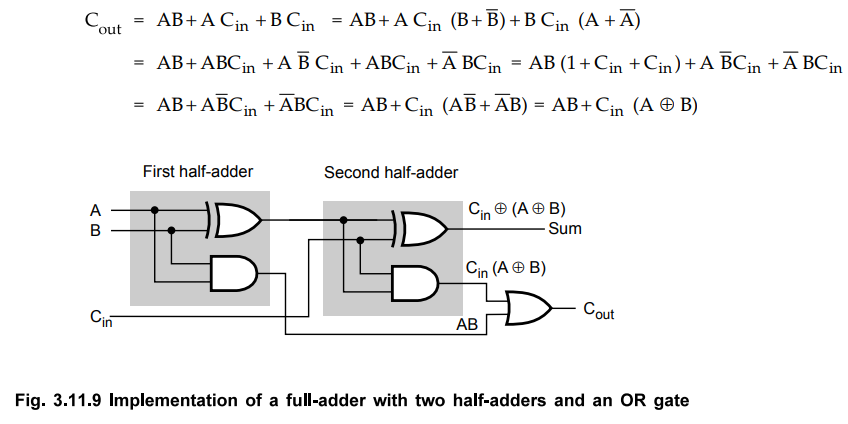
A full-adder can also be implemented with two half-adders and one OR gate, as shown in the Fig. 3.11.9. The sum output from the second half-adder is the exclusive-OR of C_in and the output of the first half-adder, giving

Review Questions

1. Define half adder and full adder.

2. Draw a block diagram of half adder. Write truth table. Draw logic diagram.

3. Write a truth table for half adder, reduce the equation using K-map and design half adder using logic gates.

4. Define full adder. Draw logic circuit and truth table of full adder.

5. Design a full adder using two half-adders and an OR gates.