Alternator On Load

Alternator On Load

Consider again two alternators running in parallel with each alternator supplying one half of active power and one half of reactive power. Each alternator supplies a load current of I such that total load current is 21. It is assumed that E1 = E2 while the operating power factor is cos and terminal voltage V. The power triangles for both the alternators can be represented as shown in Fig. 3.14.3

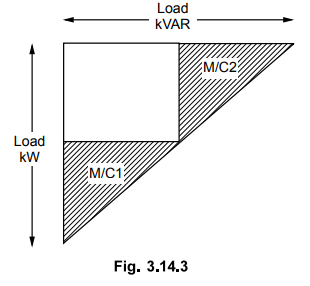
where both active and reactive powers divided equally giving apparent power triangles same.

If now excitation to alternator no. 1 is increased then its induced e.m.f. E₁ will increase which will raise the terminal voltage 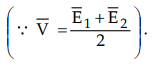. Now the difference in induced e.m.f.s will set up a circulating current I_SY = E₁ – E₂ / 2Z that flows in local circuit. This current is superimposed on original current distribution.

From the circuit diagram it can be seen that current ISY is vectorially added to the load current of alternator no. 1 and subtracted from the load current of alternator no. 2. Now the load currents will be changed to I₁ and I₂ with change in power factors. The new power factors are cos and cos ϕ₁. This is shown in the Fig. 3.14.4.

It can be seen from the Fig. 3.14.4 that cos ϕ₁ is reduced whereas cos ϕ₂ is increased. The armature currents for the two machines are changed but their active components are not changed. Thus changes in kW loading of the two alternators is negligible but reactive power kVAR₁ from first alternator is increased whereas kVAR2 supplied by second alternator is decreased which can be seen from power triangles. 

3. Phasor Diagram

The effect of change in excitation on the performance of the two alternators can be explained with the help of phasor diagram shown in the Fig. 3.14.5.

Again the two alternators are working in parallel. If now excitation of alternator 1 is increased so that its induced e.m.f. E₁ is increased to E₁ which will try to increase the terminal voltage V. But the terminal voltage V can be kept constant by decreasing the excitation of other alternator. The increase in E₁ and decrease in E2 are adjusted in such a way that E sin 8 remains constant. The difference between E₁ and E₂ will give rise to circulating current I_SY. This current must be added to I₁ and subtracted from I₂ which will give new armature currents I₁  and I₂

Induced e.m.f. are given by,

It can be seen that there is increase in magnitude of I₁ but its active component I₁ cos ϕ₁ is unaltered. Similarly I₂ is decreased in magnitude but its active component I₂ cos ϕ₂ is unaffected. Thus the load current, terminal voltage and load power factors are unchanged.

From the Fig. 3.14.5 it is clear that the alternator 1 operates at a poor p.f. which delivers greater reactive power than alternator 2 operating at a better p.f. Since the mechanical power input to the two alternators is not disturbed, the active power output is remaining same. Thus change in excitation causes only the kVAR sharing of the two alternators without disturbing kW sharing of the two machines. 

Thus the load current, the load terminal voltage and the load power factor remain unchanged but armature currents, induced e.m.f.s and operating power factors for each of the alternator is changed.

Key Point By varying the field excitation with the help of rheostats the distribution of reactive power shared by the alternators and their terminal voltage can be controlled.

4. Division of Load between Two Alternators

The division of load between the two alternators can be calculated as follows.

 From the Fig. 3.14.6 it can also be seen that

Substituting the above values in equation (3.14.1)

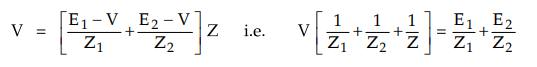
From the Fig. 3.14.6 it can also be seen that

Subtracting above two equations,

Substituting this value in equation,

Key Point When two e.m.f.s are unequal in magnitude the second term of above equation represents the circulating current under loaded conditions.

At no load (i.e. Z = ∞ ) the circulating current is given by,

I_SY = E₁ – E₂ / Z₁ + Z₂

This expression is already derived in previous section.

Review Question

1. Explain the effect of change in excitation on the load sharing of two alternators running in parallel. AU : May-04, Marks 6