Alternators Connected to Infinite Bus Bar

Alternators Connected to Infinite Bus Bar

We have already seen that synchronous generators do not operate individually in a generating station but they are interconnected so that total generating capacity will be high. When number of alternators are interconnected forming a system which may be treated as an infinite bus. Infinite bus bar is one which keeps constant voltage and frequency although the load varies. Thus it may behave like a voltage source with zero internal impedance and infinite rotational inertia. Any alternator switched on to or off, the infinite bus does not cause any change in the voltage and frequency of the system.

The characteristics of a synchronous generator on infinite bus bars are quite different from those when it is connected to another alternator and both are in parallel. When two alternators are connected in parallel we have seen that a change in the excitation changes the terminal voltage and p.f. is determined by load. However change in excitation for an alternator connected to infinite bus bar will not change the terminal voltage but the power factor only is affected whereas the power developed by an alternator depends only on mechanical power input.

Now we will consider the effect of excitation and driving torque on the performance of an alternator which is connected to infinite bus bar. In all the further discussion we will take zero losses for the machine.

1. Effect of Excitation

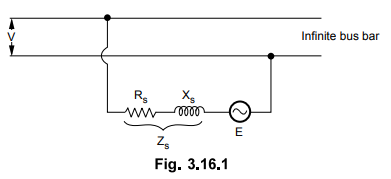
Let us consider the cylindrical rotor alternator as shown in Fig. 3.16.1 connected to infinite busbar.

The voltage equation can be written as

where          E = Induced e.m.f. or excitation e.m.f.

V = Constant bus voltage

I - Armature current

Z_s - Synchronous impedance

The same equation neglecting the armature resistance can be rewritten as,

Again we will consider the two cases one with alternator on no load and other with alternator on load.

a. Alternator on No Load

Since we are considering the losses to be zero the power angle δ will be zero. Thus the power transferred from or to the bus is zero

Now if the excitation is properly adjusted at no load then induced e.m.f. E will be equal to bus voltage V and no current will flow. This is shown in Fig. 3.16.2.

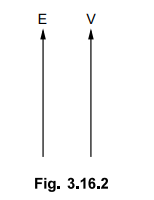
This is floating condition of alternator.

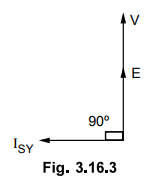
Now if the alternator is under excited then induced e.m.f. E will be less than V. This will cause circulating current IgY to flow which will lead E by angle of 90°. Due to this it produces magnetizing m.m.f. which will try to increase field m.m.f. to maintain alternator terminal voltage equal to the bus bar voltage. This is shown in following Fig. 3.16.3.

Similarly if alternator is over excited then induced e.m.f. E will be more than V which will again cause a circulating current I_SY to flow. The power angle δ is zero. This current lags E by 90^o. This will produce demagnetizing armature m.m.f. which will counterbalance the effect of increased field m.m.f and again the terminal voltage of an alternator will be equal to constant bus bar voltage V. This is represented in Fig. 3.16.4

It can be seen that in both the cases considered above, no active power is delivered since I_SY is in quadrature with V and load angle δ is also zero. But alternator takes reactive power from bus since E < V and delivers it to bus if E > V.

b. Alternator on Load

Now let us consider that alternator is supplying power to an infinite bus which has induced e.m.f. E, power angle δ and working at unity power factor with current I.

With mechanical power input to the alternator remaining constant, the power given by EV /X_s sin δ will remain constant. If by varying excitation induced e.m.f. E is increased to E₁ then the load angle will also change from δ to δ₁. From the phasor diagram it can be determined as E₁ sin δ₁ = E sin δ as V and X_s are constant. The drop due to synchronous reactance also increases and armature current increases from I to I_1. This current has two components one real component and other quadrature component. This quadrature component is nothing but demagnetizing component. This will result in lagging power factor cos ϕ₁

Similarly if the excitation is decreased so that induced e.m.f. reduces from E to E₂ with corresponding change in power angle from δ to δ₂. The armature current in this case will be I₂ which has real component and magnetizing component which results in leading power factor cos ϕ₂ . This can be represented in the phasor diagram shown in Fig. 3.16.5.

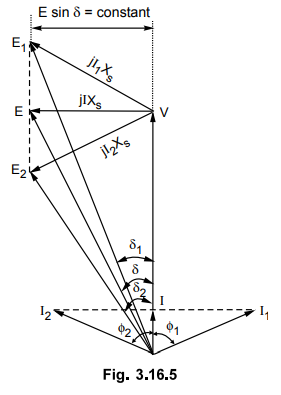
From the phasor diagram it can be seen that

I₁ cos ϕ₁ = I₂ cos ϕ₂ = I

Multiplying by V throughout,

V I₁ cos ϕ₁ = V I₂ cos ϕ₂ = V I

This indicates that power delivered to the bus will remain constant. Thus by changing the field excitation the active power is unaltered. But change in excitation results in corresponding operating power factor as shown in phasor diagram.

Key Point : An under excited alternator operates at leading power factor whereas an over excited alternator operates at lagging power factor.

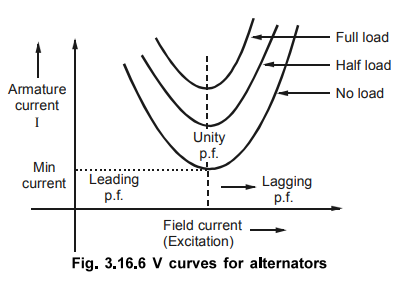
It can also be seen that armature current is minimum at unity power factor. For over excited alternator as E1 cos δ > V therefore as seen from case (i) i.e. no load condition alternator delivers reactive power to the bus where as for underexcited alternator E₂ cos δ < V,          alternator takes reactive power from the bus. This variation of excitation and armature current can be plotted as shown in Fig. 3.16.6. This is known as V curves for synchronous generators by virtue of their shape.

2. Effect of Driving Torque

As already discussed in the previous section the driving torque of an alternator can be changed by throttle opening in steam power plants and by gate opening in case of hydrogeneration. Let us see the effect of driving torque on performance of alternator with the help of phasor diagram as shown in Fig. 3.16.7.

The voltage equation remains same as

The load angle is δ. Now if the driving torque of alternator is increased keeping excitation constant then output EV / X_s sin δ also increases as δ is changing, but E, V and X_s are constant. The angle δ increases so as to balance between increased mechanical input and the power  EV / X_s sin δ . Thus the tip of phase E follows a curved path. The maximum value of δ will be 90° for which armature current is I₁ leading the bus bar voltage V by power factor angle ϕ₁.

Thus with increase in input the alternator delivers more power to infinite bus. The frequency and terminal voltage of an alternator remains same as it is connected to infinite bus bar.

If driving torque is decreased, the power angle δ must decrease correspondingly. If it becomes zero, no power is transferred to the infinite bus. The prime mover will only supply the losses.

If driving torque is reversed or if the prime mover is decoupled from the shaft E shifts and lags behind V, then 8 will be reversed and the operation of machine will change from synchronous generator to synchronous motor as now . The synchronous motor operates at a leading p.f. indicating that it is delivering reactive power to infinite bus.

Example : A 3 phase, 11 kV, 2 MV A, turbo alternator is delivering full load at 0.8 pf lagging. It has a synchronous reactance of 20 % and the resistance is negligible. If the excitation is increased by 25 % keeping the input power constant, calculate the new current and the powerfactor. The machine is connected to infinite bus bars. 

Solution :

Example for Practice

Example 3.16.2 A 6600 V, 1200 kVA, 3-phase alternator is delivering full-load at 0.8 p.f. lagging. Its reactance is 25 % and resistance negligible. By changing the excitation, the e.m.f. is increased by 30 % at this load. Calculate the new values of current and power factor. The machine is connected to infinite busbars.

[Ans.: 0.3687 lagging, I_a2 = 227.758 A]

Reivew Question

1. Explain the effect of change in excitation and driving torque on an alternator connected to infinite bus bar.