Anna university solved problem

ANNA UNIVERSITY SOLVED PROBLEM

Problem 2.3

Use Fermi distribution function to obtain the value of F(E) for E-E_F=0.01 eV at 200 K. do (A.U. May 2015)

Given data

E – E_F = 0.01 eV = 0.01 × 1.6 × 10^-19 J = 1.6 × 10^-21 J

Temperature T = 200 K

Boltzmann's constant k = 1.38 × 10^-23 JK^-1

Solution

We know that F (E):

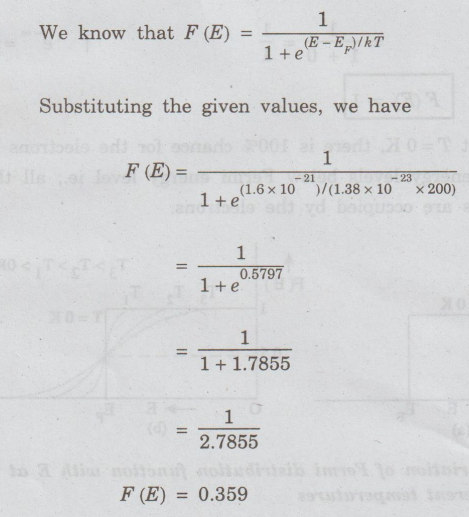
=1 / 2.7855

F (E) = 0.359

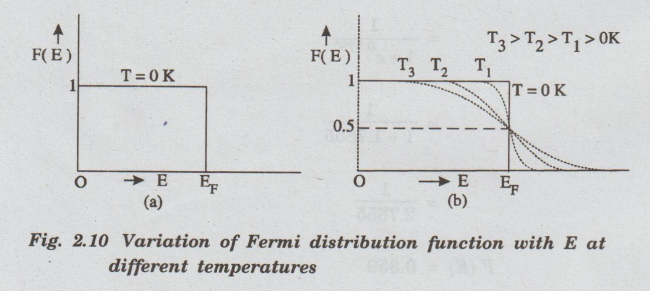
Effect of Temperature on Fermi Function

The dependence of Fermi - distribution function on temperature and its effect on the occupancy of energy level is shown in fig. 2.10 (a) and (b). 2.10 (a)

Case (i) Probability of occupation for E <E_F at T=0 K

When T = 0 K and E < E_F then applying the values in the expression, we have

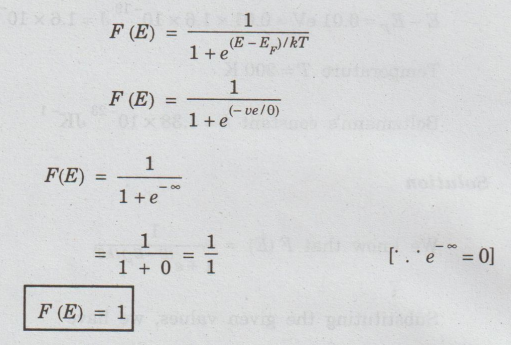
F(E) = 1

Thus at T=0 K, there is 100% chance for the electrons to occupy the energy levels below Fermi energy level ie., all the energy levels are occupied by the electrons.

Case (ii) Probability of occupation for E > E_F at T=0 K

When T = 0 K and E > E_F, then applying the values in the expression F (E) =

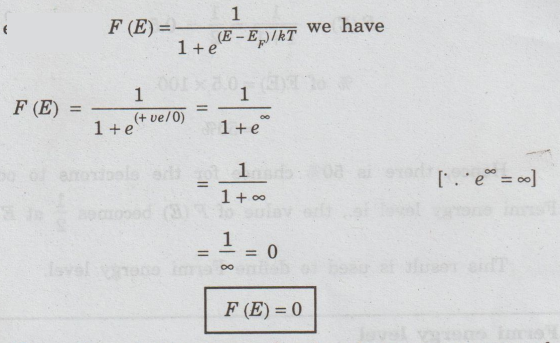
F (E) = 0

Thus, there is 0% chance for the electrons to occupy the energy level above Fermi energy level ie., all the energy levels above Fermi energy level are not occupied by the electrons (empty).

From the above two cases, at T= 0K the variation of F (E) for different energy values become a step function as shown in fig 2.10(a).

Case (iii) Probability of occupation at ordinary temperature

At ordinary temperature, the value of the probability function starts reducing from 1 for energy values E slightly less than E_F.

With the increase of temperature, i.e., T >0 K, Fermi function F (E) varies with E as shown in fig. 2.10(b).

At any temperature other than OK and E=E_F

F(E) = 1 / 1+e⁰

F(E) = 1/ 1+1 = ½ =0.5  e⁰ = 1

% of F(E)=0.5 × 100

= 50%

Hence, there is 50% chance for the electrons to occupy Fermi energy level ie., the value of F (E) becomes ½ at E = E_F

This result is used to define Fermi energy level.

Fermi energy level

• It is the energy level at any finite temperature above 0K at which the probability of electro occupation is ½ or 50%.

• It is also the energy level of maximum energy of the filled states at 0 K.

 Further for E> E_F the probability value falls off rapidly to zero (Fig 2.10(b)).

Case (iv) At high temperature

When kT >> E_F or T → ∞, the electrons lose their Baal vir quantum mechanical character. Now, Fermi distribution east function reduces to classical Boltzmann distribution.

Uses of Fermi distribution function

• It gives the probability of an electron occupancy for a given energy level at a given temperature.

• It is very useful to find the number of free electrons per unit volume at a given temperature.

• It is used to find Fermi energy of the metal.