Electric Circuit Analysis: Unit IV: Three phase circuits
Balanced delta connected load
Three phase circuits
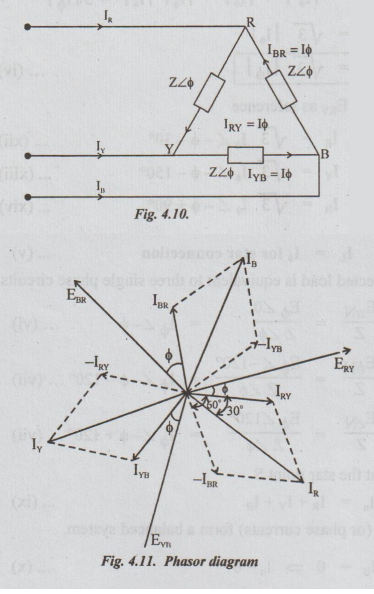
Fig.4.10 shows a balanced delta - connected load of impedance Z in each phase.
BALANCED DELTA CONNECTED LOAD
Fig.4.10
shows a balanced delta - connected load of impedance Z in each phase.
Z
= | Z| ∠ϕ
The
phasor diagram is also shown in fig.4.10.
Assume
the phase sequence to be RYB. Taking ERY as reference
Expression
for total power in a 3 phase balanced circuit
Let
E ϕ
= Voltage per phase
I
ϕ
= Current per phase
cos
ϕ Power factor of the balanced load
Total
average power W = 3 E ϕ Iϕ cos ϕ … (i)
Usually,
this expression is expressed in terms of line voltage and line current as
below:
Case
(1):
Star connected load:
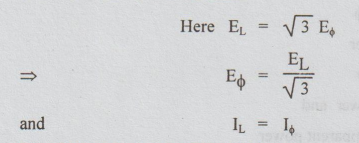
Substituting
these values in equation (i)
Case
(2): Delta connected load:
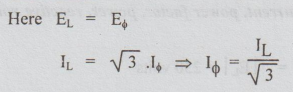
Putting
these values in equation (i), we get
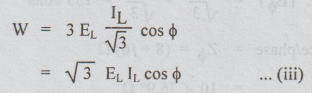
EL
and IL are in volts and amperes respectively.
Then
the power W is in watts. Dividing both sides of the equation (iii) by 1000, we
get:
W
/ 1000 = √3EL IL /
1000 cos ϕ
W/1000
is actual power or average power or a real power or true power. (denoted by P)
in KW.
√3EL
IL / 1000 is apparent power (denoted by S) and measured in KV
amperes (KVA).
KW
= KVA cos ϕ ... (iv)
From
equation (iv), we can draw the power triangle which is shown below:
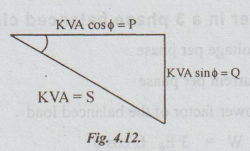
It
is right-angled triangle from which we get the relation S = P + jQ
⇒ S = √ P2 +
Q2 …. (v)
Here
P = KVA cos ϕ
=
active power
Q
= KVA sin ϕ
=
reactive power and
S
= KVA = apparent power
Electric Circuit Analysis: Unit IV: Three phase circuits : Tag: : Three phase circuits - Balanced delta connected load
Electric Circuit Analysis: Unit IV: Three phase circuits
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation