Barkhausen Criterion for Oscillators

Barkhausen Criterion for Oscillators

• For an oscillator, there is no input (Vs = 0) hence feedback voltage Vf must be sufficient to maintain the oscillations.

• To ensure this, oscillator must satisfy the criterion called Barkhausen criterion.

• Consider an inverting amplifier producing 180° phase shift between input and output.

• To ensure positive feedback, there must be further 180° phase shift between output Vo and feedback voltage Vf. Thus the feedback voltage is in phase with input ensuring positive feedback.

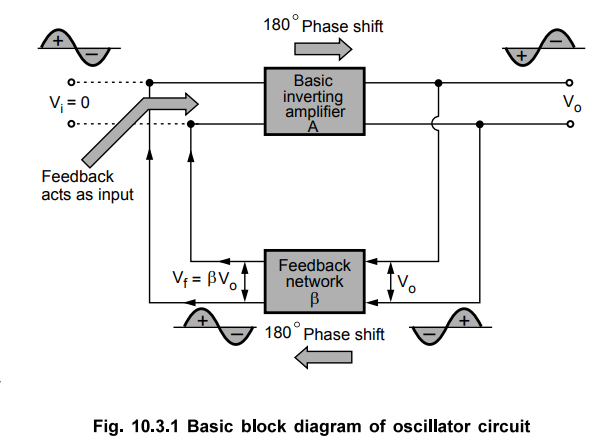
• The arrangement is shown in the Fig. 10.3.1 where fictitious voltage Vi is applied at the input of the amplifier.

• Vo = A Vi while Vf = - β Vo where negative indicates 180° phase shift between Vo and Vf.

V_f = -A β V_i

• For oscillator, V_i = 0 and V_f must drive the circuit hence V_f = V_i

• The condition -A β = 1 is called Barkhausen condition.

• From equation (10.3.1) we can write, A β = -1 + j0 hence equating magnitudes,

| A β | = 1    ... (10.3.2)

• And to have phase of Vf same as phase of Vf i.e. positive feedback, total phase shift around a loop must be 180° by forward path +180° by feedback path i.e. 360°.

• The two conditions discussed above, required to work the circuit as an oscillator are called Barkhausen criterion for oscillation.

The Barkhausen criterion states that :

1. The total phase shift around a loop, as the signal proceeds from input through amplifier, feedback network back to input again, completing a loop, is precisely 0° or 360°, or of course an integral multiple of 2π radians.

2. The magnitude of the product of the open loop gain of the amplifier (A) and the feedback factor β is unity i.e. | A β | =1.

• Satisfying these conditions, the circuit works as an oscillator producing sustained oscillations with constant frequency and amplitude.

• In reality no input is required. To overcome energy loss initially | A β | is adjusted slightly greater than 1 and then circuit adjusts itself to get | A β | = 1, to produce oscillations.

1. Effect of |Aβ |  on Oscillations

• When total phase shift around a loop is 0° or 360° and |A β | > 1 then the output oscillations are of increasing amplitude as shown in the Fig. 10.3.2 (a), making system unstable.

• When total phase shift around a loop is 0° or 360° and |A β | < 1 then oscillations are damped with decreasing amplitude as shown in the Fig. 10.3.2 (b).

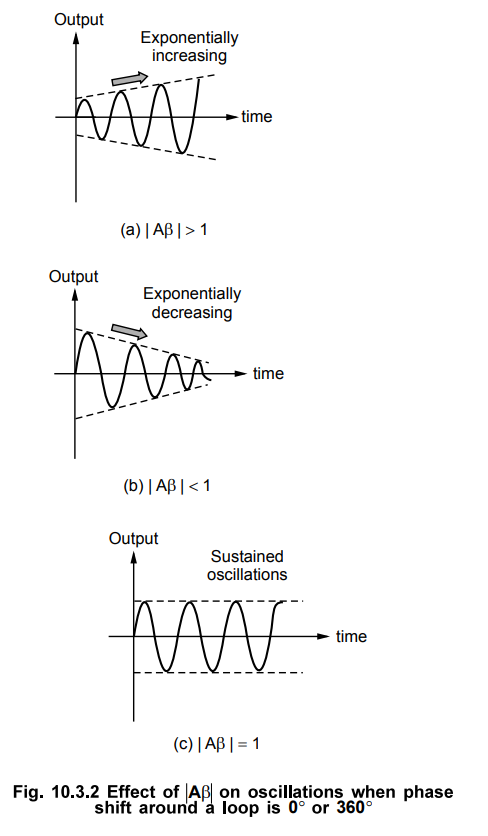 • When total phase shift around a loop is 0° or 360° and | A β | = 1 i.e. Barkhausen conditions are satisfied then circuit works as an oscillator producing sustained oscillations as shown in the Fig. 10.3.2 (c).

2. Frequency of Oscillations

• The frequency at which circuit satisfies both the Barkhausen conditions i.e.| A β | = 1 and ∠A β = 0° or 360° simultaneously is called frequency of oscillations.

3. Starting Voltage

• For oscillators, external input is zero then how oscillators produce output ?

• Every electronic component such as resistance has free electrons which move randomly inside the component.

• Such a random movement of free electrons in various directions produces a voltage called noise voltage.

• Such a noise voltage is amplified by the amplifier and fed back at the input.

• As this voltage is small, initially | A β | is slightly greater than one so that amplified noise voltage appears at the output.

• The part of this voltage is sufficient to drive the circuit and then circuit adjusts itself to get |A β| = 1 and starts working as an oscillator without any external input.

Review Question

1. Explain the Barkhausen criterion in detail.