Digital Logic Circuits: Unit II: Combinational Circuits
Boolean Algebra
Terminology, Postulates and Laws, Boolean Theorems, Truth table, Example Problems
• In 1854, George Boole introduced a systematic treatment of logic and developed for this purpose an algebraic system now called Boolean algebra. • Boolean algebra is a system of mathematical logic. It differs from both ordinary algebra and the binary number system.
Review of Boolean Algebra
•
In 1854, George Boole introduced a systematic treatment of logic and developed
for this purpose an algebraic system now called Boolean algebra.
•
Boolean algebra is a system of mathematical logic. It differs from both
ordinary algebra and the binary number system.
1. Boolean Algebra Terminology
Variable
:
The symbol which represent an arbitrary elements of an Boolean algebra is known
as variable. Any single variable or a function of several variables can have
either a 1 or 0 value. For example, in expression Y = A + BC, variables A, B
and C can have either a 1 or 0 value, and function Y also can have either a 1
or 0 value; however its value depends on the value of Boolean expression.
Constant
:
In expression Y = A + 1, the first term A is a variable and have value either a
1 or 0. The second term has a fixed value 1. So 1 is a constant here. The
constant term may be 0 or 1.
Complement
:
A complement of a variable is represented by a "bar" over the letter.
For example, the complement of a variable A will be denoted by 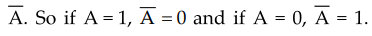 .
Sometimes a prime symbol (') is used to denote the complement. For example, the
complement of A can be written as A'.
.
Sometimes a prime symbol (') is used to denote the complement. For example, the
complement of A can be written as A'.
Literal
:
Each occurrence of a variable in Boolean function either in a complemented or an
uncomplemented form is called a literal.
Boolean
function : Boolean expressions are constructed by connecting
the Boolean constants and variables with the Boolean operations. These Boolean
expressions are also known as Boolean formulas. We use Boolean expressions to
describe Boolean functions. For example, if the Boolean expression 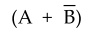 C is used to describe the function f, then
Boolean function is written as
C is used to describe the function f, then
Boolean function is written as
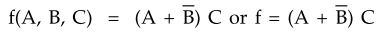
2. Fundamental Postulates and Laws Boolean Algebra
The
postulates of a mathematical system form the basic assumption from which it is
possible to deduce the theorems, laws and properties of the system. Boolean
algebra is formulated by a defined set of elements, together with two binary
operators, + and • , provided that the given postulates are satisfied.
•
Closure (a) : Closure with respect to the operator +
: When two binary elements are operated by operator + The result is a unique
binary element.
•
Closure (b) : Closure with respect to the operator.
(dot) : When two binary elements are operated by operator • (dot), the result
is a unique binary element.
•
An identity element with respect to +, Designated by 0: A + 0 = 0 + A = A
•
An identity element with respect to ,
Designated by 1 : A .1 = 1.A = A
•
Commutative with respect to + : A + B = B + A
•
Commutative with respect to .: A . B = B . A
•
Distributive property of . over + :
A
.(B + C) = (A . B) + (A . C)
•
Distributive property of + over . :
A
+ (B . C) = (A + B) . (A + C)
•
Associative property of + :
A
+ (B + C) = (A + B) + C
•
Associative property of •: (A . B) . C = A . (B . C)
•
For every binary element, there exists complement element. For example, if A is
an element, we have
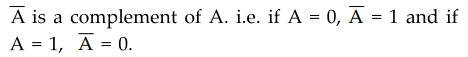
•
There exists at least two elements, say A and B in the set of binary elements
such that A ≠B.
From
the above discussion we can summarize the Huntington's postulates of Boolean
algebra as shown in Table. 3.1.1.

3. Boolean Theorems
a.
Duality
The
principle of duality theorem says that, starting with a Boolean relation, you
can derive another Boolean relation by
1.
Changing each OR sign to an AND sign
2.
Changing each AND sign to an OR sign and
3.
Complementing any 0 or 1 appearing in the expression.
For
example : Dual of relation 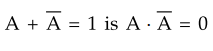
b.
Basic Theorems
The
Table 3.1.2 lists the five basic theorems of Boolean algebra four of its
postulates. The postulates and theorems are listed in pairs and designated by
part (a) and part (b). One part may be obtained from the other by using
principle of duality.

c. DeMorgan's Theorems
•
DeMorgan suggested two theorems that form an important part of Boolean algebra.
In the equation form, they are:
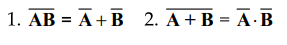
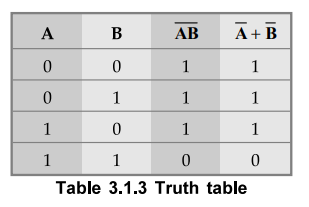
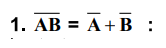 The complement of a product is equal to
the sum of the complements. This is illustrated by truth Table 3.1.3.
The complement of a product is equal to
the sum of the complements. This is illustrated by truth Table 3.1.3.
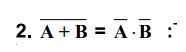 The complement of a sum is equal to the
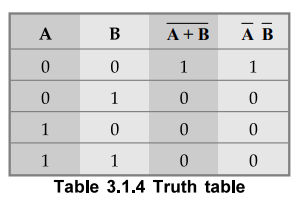
product of the complements. The truth Table 3.1.4 illustrates this law.
The complement of a sum is equal to the
product of the complements. The truth Table 3.1.4 illustrates this law.
Examples for Understanding
Ex.
3.1.1 Simplify : x + x'y.
AU
: Dec.-07, May-10, Marks 2
Sol.
:
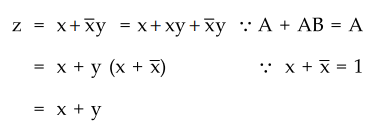
Ex.
3.1.2 Simplify the expression 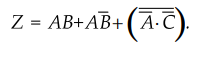
AU
: May-15, Marks 2
Sol.
:
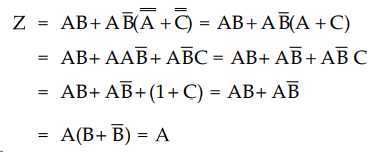
Ex.
3.1.3 Prove the following Boolean identities.
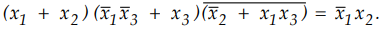
AU
: May-03, 08, Marks 8
Sol.
:
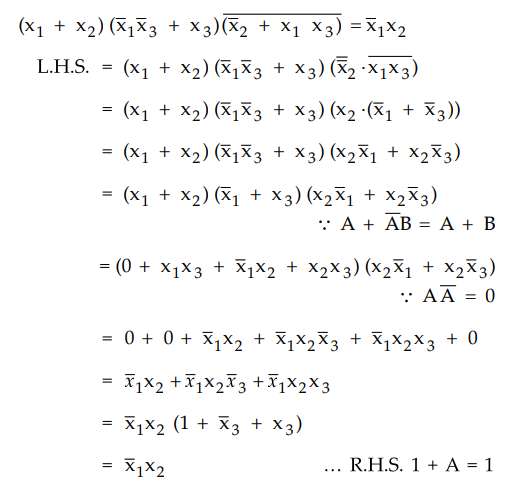

Examples
for Practice
Ex.
3.1.5 Simplify the following Boolean expressions to a minimum number of
literals : AU : Dec.-05, Marks 2

Ex.
3.1.6 Simplify the following Boolean expression,
AU
: May-05, Marks 2
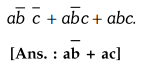
Ex
. 3.1.7 Simplify the following Boolean expressions to a minimum number of
literals:
AU
: Dec.-05, Marks 2
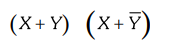
[Ans.
: X]
Review Questions
1. What are Boolean variables ?
2. Define the following terms : Boolean variable, complement,
literal.
3. State the fundamental postulates of Boolean algebra
4. State various laws of Boolean algebra.
5. State the associative law of Boolean algebra.
AU : May-08, Marks 2
6. Explain the principle of duality with the help of example
7. State and prove DeMorgan’s theorem.
DAU : ec.-08, Marks 8
8. Write brief note on the following : DeMorgan’s theorem.
AU : Dec.-ll, Marks 4
Digital Logic Circuits: Unit II: Combinational Circuits : Tag: : Terminology, Postulates and Laws, Boolean Theorems, Truth table, Example Problems - Boolean Algebra
Related Topics
Related Subjects
Digital Logic Circuits
EE3302 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
