Boundary Conditions between Conductor and Free Space

Boundary Conditions between Conductor and Free Space

AU : May-10, 18, Dec.-13, 18

• Consider a boundary between conductor and free space. The conductor is ideal having infinite conductivity. Such conductors are copper, silver etc. having conductivity of the order of 10⁶ S/m and can be treated ideal. For ideal conductors it is known that,

1. The field intensity inside a conductor is zero and the flux density inside a conductor is zero.

2. No charge can exist within a conductor. The charge appears on the surface in the form of surface charge density.

3. The charge density within the conductor is zero.

• Thus 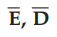 and ρv within the conductor are zero. While ρ S is the surface charge density on the surface of the conductor.

• To determine the boundary conditions let us use the closed path and the Gaussian surface.

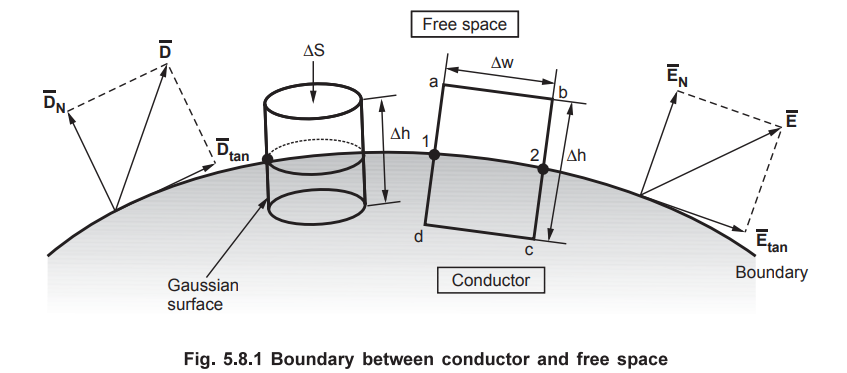
• Consider the conductor free space boundary as shown in the Fig. 5.8.1.

 

1. 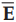 at the Boundary

• Let  be the electric field intensity, in the direction shown in the Fig. 5.8.1, making some angle with the boundary. This  can be resolved into two components :

1. The component tangential to the surface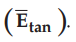

2. The component normal to the surface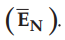 

It is known that,

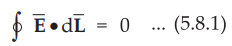
• The integral of 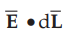 carried over a closed contour is zero i.e. work done in carrying unit positive charge along a closed path is zero.

• Consider a rectangular closed path  as shown in the Fig. 5.8.1. It is traced in clockwise direction as a-b-c-d-a and hence 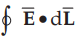 can be divided into four parts.

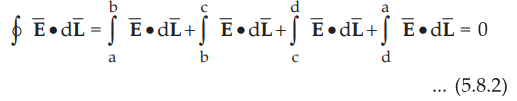
• The closed contour is placed in such a way that its two sides a-b and c-d are parallel to tangential direction to the surface while the other two are normal to the surface, at the boundary.

• The rectangle is an elementary rectangle with elementary height A and elementary width Aw. The rectangle is placed in such a way that half of it is in the conductor and remaining half is in the free space. Thus ^/2 is in the conductor and Δh/2 is in the free space.

• Now the portion c-d is in the conductor where  = 0 hence the corresponding integral is zero.

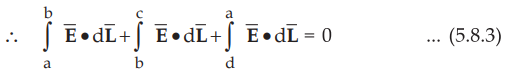
• As the width Aw is very small, E over it can be assumed constant and hence can be taken out of integration.

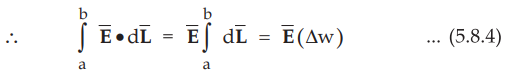
• But Δw is along tangential direction to the boundary in which direction

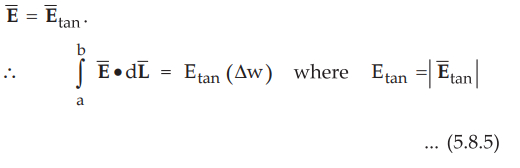
• Now b-c is parallel to the normal component so we have 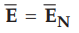 along this direction. Let .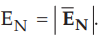

• Over the small height  Δh, E_N can be assumed constant and can be taken out of integration.

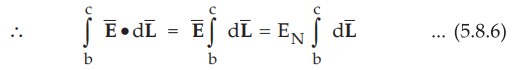
• But out of b-c, b-2 is in free space and 2-c is in the conductor where  = 0.

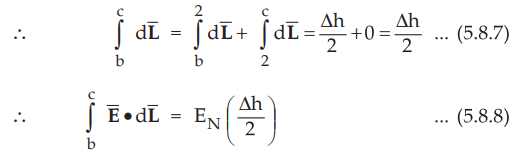
• Similarly for path d-a, the condition is same as for the path b-c, only direction is opposite.

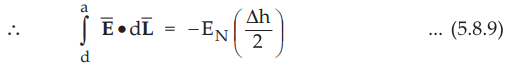
Substituting equation (5.8.4), (5.8.8) and (5.8.9) in (5.8.3) we get,

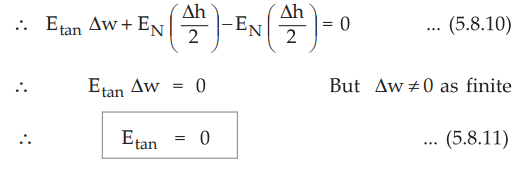
• Thus the tangential component of the electric field intensity is zero at the boundary between conductor and free space.

Key Point : Thus the  at the boundary between conductor and free space is always in the direction perpendicular to the boundary.

• Thus the tangential component of electric flux density is zero at the boundary between conductor and free space.

Key Point : Hence electric flux density  is also only in the normal direction at the boundary between the conductor and the free space.

 

2. D_N at the Boundary

• To find normal component of , select a closed Gaussian surface in the form of right circular cylinder as shown in the Fig. 5.8.1. Its height is Ah and is placed in such a way that Δh/2 is in the conductor and remaining Δh/2 is in the free space. Its axis is in the normal direction to the surface.

• According to Gauss's law,

• The surface integral must be evaluated over three surfaces,

i) Top, ii) Bottom and iii) Lateral.

• Let the area of top and bottom is same equal to ΔS.

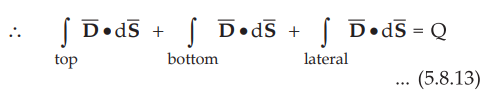
• The bottom surface is in the conductor where  = 0 hence corresponding integral is zero.

• The top surface is in the free space and we are interested in the boundary condition hence top surface can be shifted at the boundary with Δh → 0.

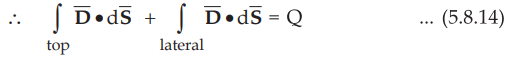
• The lateral surface area is 2 π r Δh where r is the radius of the cylinder. But as Δh → 0, this area reduces to zero and corresponding integral is zero.

• While only component of  present is the normal component having magnitude D_N The top surface is very small over which D_N can be assumed constant and can be taken out of integration.

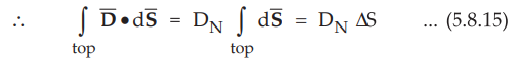
From Gauss's law,

D_N ΔS = Q  ... (5.8.16)

• But at the boundary, the charge exists in the form of surface charge density ρS C / m².

Q = ρS ΔS …. (5.8.17)

Equating equation (5.8.16) and (5.8.17),

D_N ΔS = ρS ΔS

D_N  = ρS ... (5.8.18)

• Thus the flux leaves the surface normally and the normal component of flux density is equal to the surface charge density.

D_N  = Ɛ₀ E_N  = ρS ... (5.8.19)

EN = ρS / Ɛ₀ ... (5.8.20)

Key Point : Note that as the tangential component of , the surface of the conductor is an equipotential surface. The potential difference along any path on the surface of the conductor is  the potential difference is zero. Thus all points on the conductor surface are at the same potential.

 

3. Boundary Conditions between Conductor and Dielectric

• The free space is a dielectric with Ɛ = Ɛ₀. Thus if the boundary is between conductor and dielectric with Ɛ = Ɛ₀ Ɛ_r.

 

Ex. 5.8.1 A potential field is given as V = 100 e^-5x sin 3y cos 4z V.

Let point P (0.1, π/12, π/24) be located at a conductor free space boundary. At point P, find the magnitudes of,

 

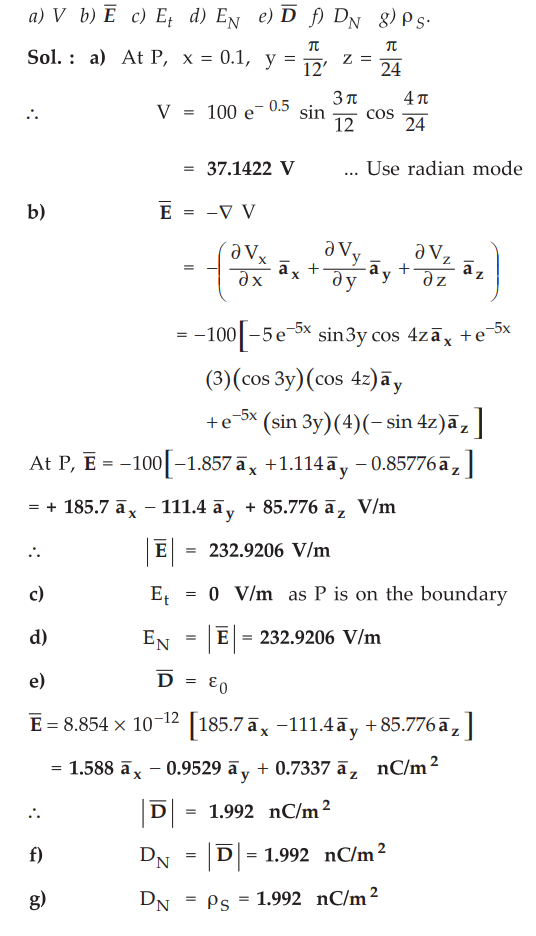
Examples for Practice

Ex. 5.8.2 The electric field intensity at a point on the surface of a conductor is given by

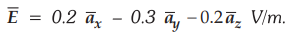
Find the surface charge density at that point.

[Ans.: 3.6506 pC/m²]

Ex. 5.8.3 Given the potential V = 10 (x² + xy) and a point P(2, - 1, 3) on a conductor to free space boundary find 

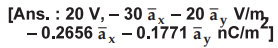
Review Question

1. Explain and derive the boundary conditions for a conductor free space interface.