Parallel Plate Capacitor

Parallel Plate Capacitor

AU : May-95, 04, 06, 10, 14, 17

• A parallel plate capacitor is shown in the Fig. 5.13.1. It consists of two parallel metallic plates separated by distance 'd'. The space between the plates is filled with a dielectric of permittivity Ɛ. The lower plate, plate 1 carries the positive charge and is distributed over it with a charge density + ρs. The upper plate, plate 2 carries the negative charge and is distributed over its surface with a charge density - ρs. The plate 1 is placed in z = 0 i.e. xy plane hence normal to it is z direction. While upper plate 2 is in z = d plane, parallel to xy plane.

• Let A = Area of cross section of the plates in m²

• This is magnitude of charge on any one plate as charge carried by both is equal in magnitude. To find potential difference, let us obtain   between the plates.

• Assuming plate 1 to be infinite sheet of charge,

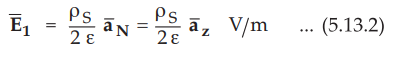
• The  is normal at the boundary between conductor and dielectric without any tangential component.

• While for plate 2, we can write

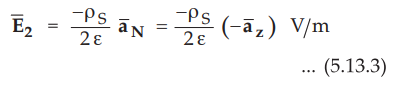
• The direction of  is downwards i.e. in -  direction.

In between the plates,

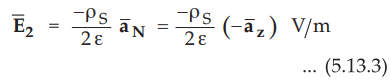
The potential difference is given by,

It can be seen that the value of capacitance depends on,

1. The permittivity of the dielectric used.

2. The area of cross section of the plates.

3. The distance of separation of the plates.

It is not dependent on the charge or the potential difference between the plates.

Ex. 5.13.1 Determine the value of capacitance between 2 square plates cross sectional area 1 sq. cm separated by 1 cm placed in a liquid whose die-electric constant is 6 and the relative permittivity of free space is 8.854 pF/m.

AU ; May-04, Marks 4

Sol. :

Ex. 5.13.2 A parallel plate capacitor has an area of 08 m2, separation of 0.1 mm with a dielectric for which £r = 1000 and a field of 10⁶ V/m.

Calculate C and V.

Solution :

Ex, 5.13,3 The relative permittivity of dielectric in a parallel plate capacitor varies linearly from 4 to 8. If distance of separation of plates is 1 cm and area of cross section of plates is 12 cm2, find the capacitance.

Sol. : The arrangement is shown in the Fig. 5.13.2.

The Ɛr varies linearily from 4 to 8, along x direction. The equation for linear behaviour is,

Ex. 5.13.4 The capacitance of the condenser formed by the two parallel metal sheets, each 100 cm in area separated by a dielectric 2 mm thich is 2 × 10^-4 µF. A potential of 20 kV is applied to it. Find :

a) Electric flux b) Potential gradient in kV/m c) The relative permittivity of the material and d) Electric flux density.

AU : May-95, 06, Marks 8

Sol. :

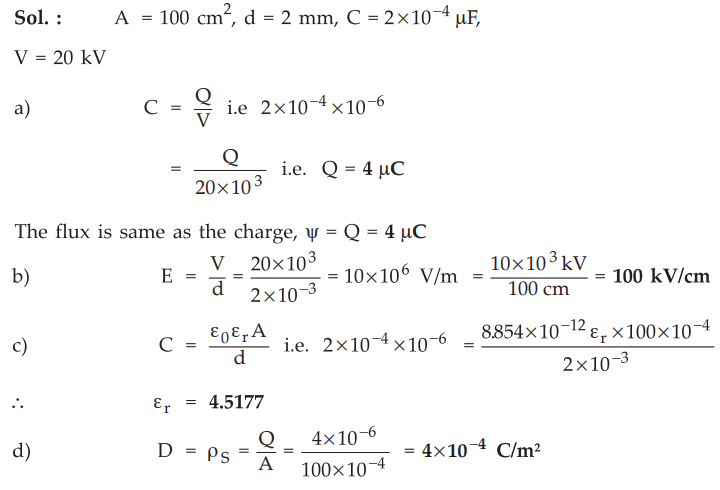
Ex. 5.13.5 Find the capacitance between two parallel conductors, mtrs. Both wire are carrying the current in opposite direction.

Sol. : The arrangement of the conductors is shown in the Fig. 5.13.3. 

The conductors are carrying currents in opposite directions. Consider point P at a distance x from the conductor A. The fields acting at point P due to both the conductors are in same directions. The magnitudes of the fields at point P due to both the conductors are,

Examples for Practice

Ex. 5.13.6 The capacitance of the condenser formed by the two parallel metal sheets, each 100 cm2 in area separated by a dielectric 2 mm thich is 2 × 10^-4 µF. LIF. A potential of 20 kV is applied to it. Find :

a) Electric flux b) Potential gradient in kV/m c) The relative permittivity of the material and d) Electric flux density.

[Ans.: 4 iiC, 100 kV/cm, 4.5177, 4 x 10 4 C/m2]

Ex, 5.13.7 The electric field intensify in polystyrene (Ɛ_r = 2.55) filling the space between the plates of a parallel plate capacitor is 10 kV/m. The distance between the plates is 1.5 mm. Calculate : i) The surface charge density of free charge on the plates ii) The potential difference between the plates.

[Ans.: 2.2577 × 10^-7 C/m²,15 V]

Ex. 5.13.8 Find the capacitance of a parallel plate capacitor if A = 1 m2, distance between the plates is 1 mm, voltage gradient is 10s V/m and charge density on the plate is 2 µC / m².       

[Ans.: 20 nF]

Review Question

1. Derive the expression for a capacitance of a parallel plate capacitor.