Boundary Conditions between Two Perfect Dielectrics

Boundary Conditions between Two Perfect Dielectrics

AU : May-07,08,10,12,13,17,18, Dec.-04,05,08,ll,12,13,14,17,18

• Let us consider the boundary between two perfect dielectrics. One dielectric has permittivity Ɛ₁ while the other has permittivity Ɛ₂. The interface is shown in the Fig. 5.9.1.

• The  are to be obtained again by resolving each into two components, tangential to boundary and normal to the surface.

• Consider a closed path abcda rectangular in shape having elementary height Ah and elementary width Aw, as shown in the Fig. 5.9.1. It is placed in such a way that Δh/2 is in dielectric 1 while the remaining is dielectric 2. Let us evaluate the integral of 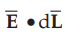  along this path, tracing it in clockwise direction as a-b-c-d-a.

 

• Both 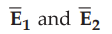 in the respective dielectrics have both the components, normal and tangential.

• Now for the rectangle to be reduced at the surface to analyse boundary conditions, Δh → 0. As  become zero as these are line integrals along Δh and Δh → 0. Hence equation (5.9.2) reduces to,

• Now a-b is in dielectric 1 hence the corresponding component of   is Et_an1 as a-b direction is tangential to the surface.

• While c-d is in dielectric 2 hence the corresponding component of   is E_tan2 as c-d direction is also tangential to the surface. But direction c-d is opposite to a-b hence corresponding integral is negative of the integral obtained for path a-b.

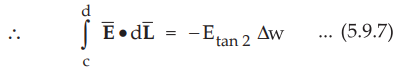
Substituting equation (5.9.6) and (5.9.7) in (5.9.5) we get,

E_tan1 Δw - E_tan2 Δw = 0

E_tan1 = E_tan2 … (5.9.7)

• Thus the tangential components of field intensity at the boundary in both the dielectrics remain same i.e. electric field intensity is continuous across the boundary.

• The relation between  is known as,

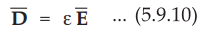
• Hence if D _{tan 1} and D _{tan 2} are magnitudes of the tangential components of   in dielectric 1 and 2 respectively then,

• Thus tangential components of   undergoes some change across the interface hence tangential   is said to be discontinuous across the boundary.

• To find the normal components, let us use Gauss's law. Consider a Gaussian surface in the form of right circular cylinder, placed in such a way that half of it lies in dielectric 1 while the remaining half in dielectric 2. The height Δh → 0 hence flux leaving from its lateral surface is zero. The surface area of its top and bottom is ΔS.

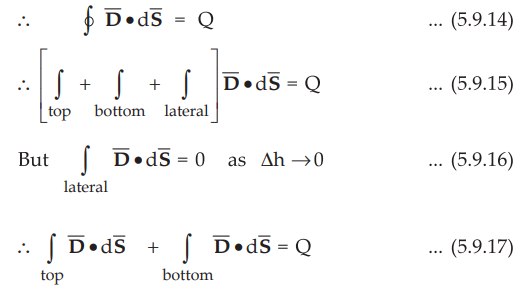
• The flux leaving normal to the boundary is normal to the top and bottom surfaces.

|   | = D_N1 for dielectric 1 and D_N2 for dielectric 2.

• And as top and bottom surfaces are elementary, flux density can be assumed constant and can be taken out of integration.

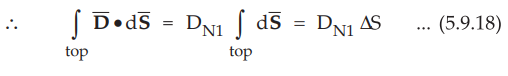
• For top surface, the direction of D_N is entering the boundary while for bottom surface, the direction of D_N is leaving the boundary. Both are opposite in direction, at the boundary.

• There is no free charge available in perfect dielectric hence no free charge can exist on the surface. All charges in dielectric are bound charges and are not free. Hence at the ideal diectric media boundary the surface charge density ρs can be assumed zero.

 

• Hence the normal component of flux density   is continuous at the boundary between the two perfect dielectrics.

• The normal components of the electric field intensity  are inversely proportional to the relative permitivities of the two media.

 

1. Refraction of   at the Boundary

• The directions of   change at the boundary between the two dielectrics.

• This is called law of refraction. Thus the angles θ₁ and θ₂ are dependent on permitivities of two media and not on .

• Thus if Ɛ₁ > Ɛ₂, then θ₁ > θ₂.

• The magnitude of   in region 2 can be obtained as,

To find the angles θ₁ and θ₂, with respect to normal use the dot product if normal direction to the boundary is known.

 

Ex. 5.9.1 The region with z < 0 is characterised by

Ɛ_r2 = 2 and z > 0 by Ɛ_r1 = 5. If

Sol. : The two media are separated by z = 0 plane and ±  are the directions of normal to the surface.

 

Ex. 5.9.2 Consider the boundary between two media. Show that the angles between the normal to the boundary and the conductivities on either side of the boundary satisfy the relation

 tan θ₁ / tan θ₂ = σ₁ / σ₂

Sol. : The arrangement is shown in the Fig. 5.9.4.

 

• The electric field intensities are  in media 1 and 2 respectively.

• As per boundary conditions,

E_tan1 = E_tan2

• While  are current densities in the two media. Similar to flux densities  the boundary condition for current densities  states that J_N1 = J_N2

 

Ex. 5.9.3 A dielectric-free space interface has the equation 3x + 2y + z = 12 m. The origin side of the interface has Ɛn = 3.0 a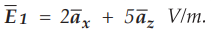nd  Find

AU : Dec.-05, Marks 10

Sol. : The interface is shown in the Fig. 5.9.5 by its intersections with axes.

 

... Unit normal vector on free space side

 

Ex. 5.9.4 The interface between a dielectric medium having relative permittivity 4 and free space is marked the y = 0 plane. If the electric field next to the interface in the free space region is given by 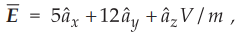 , determine   field on the other side of the interface.

AU : Dec.-11, Marks 8

Sol. : The normal direction to the y = 0, plane is  hence out of   is the normal component of 

 

 

Examples for Practice

Ex. 5.9.5 A boundary exists at z = 0 between two dielectrics Ɛ_r1 = 2.5 in region z < 0 and Ɛ_r2 = 4 in the region z > 0. The field in the    region         of Ɛ_r1  is

Find :

i) Norma! component of E}

ii) Tangential component of E1

iii) Angle between and normal to the surface (given a1 ≤ 90°)

iv) Normal component of D2

v) Tangential component of D2

vi) Angle a2 between E2 and normal to the surface

Ex. 5.9.6 A unit vector directed from region 1 to region 2 at the planar boundary between two perfect dielectrics is given as 

Ex. 5.9.7 Given that:

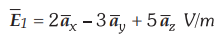
at the charge free dielectric interface as shown in Fig. 5.9.7 below.

Find and angles θ₁ θ₂.

Review Questions

1. Derive the conditions at a boundary between the interface of the two dielectrics in electric field.

AU : Dec.-04,05,08,12,13,17,18, May-07,08,10,17,18, Marks 8

2. Explain the law of refraction at dielectric-dielectric interface.

3. At an interface separating dielectric l(Ɛrl) and dielectric 2(Ɛr2) show that the tangential component of   is continuous across the boundary, whereas the normal component of   is discontinuous at the boundary.

AU : May-13, Dec.-14, Marks 10