Calculation of area by offsets from base line

CALCULATION OF AREA BY OFFSETS FROM BASE LINE

This method is convenient to determine the area between a base line and a long irregular boundary. The area can be determined by the following 

RULES:

1. RULE I: MID-ORDINATE RULE

See Fig. 46.

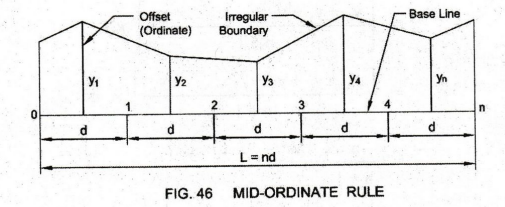
In this method, the Base Line is divided into a number of equal divisions (n) of length (d).

It is assumed that the boundary between successive Offsets (Ordinates) is a straight line.

Ordinates (offsets) yı, y2, y3, ... . Yn are measured from the middle point of each division.

Total length of the base line = L = nd

Area = Average Ordinate Length × Length of the Base Line

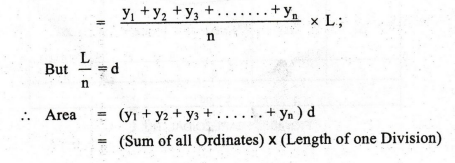
 (Sum of all Ordinates) × (Length of one Division)

2. RULE II: MEAN ORDINATE RULE or AVERAGE ORDINATE RULE

See Fig. 47.

This method makes the same assumption as the previous method.

In this method, the Ordinates (Perpendicular Offsets) yo, y1, y2, .... Yn are drawn at each point of the division of the base line.

Total length of the base line = L = nd; where n is the Number of divisions into which the base line is divided and d is the Length of each division

Total Number of Ordinates (Offsets) = n +1

Area = Average Ordinate Length × Length of the Base Line

The above two methods are not accurate. More accurate methods are given below.

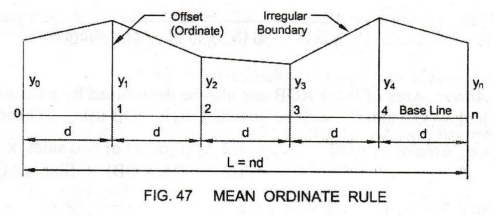
3. RULE III: TRAPEZOIDAL RULE

See Fig. 48.

In this method, the area between the boundary and the base line is assumed to consist a number of Trapeziums.

On this assumption, the area between the boundary and the base line is calculated.

The rule is more accurate than the previous two rules which are the approximate versions of the trapezoidal rule.

Total length of the base line = L = nd; where n is the Number of divisions into which the base line is divided and d is the Length of each division

Total Number of Ordinates (Offsets) = n + 1

Thus, the Trapezoidal Rule is stated as: "Add the average of the end ordinates (offsets) to the sum of the intermediate ordinates (offsets). Multiply the result by the common distance between the ordinates (offsets) to get the required area."

4. RULE IV: SIMPSON'S RULE

Simpson's Rule assumes that the short lengths of the boundary between the ordinates are curved lines and are considered as portions of parabolic arcs.

See Fig. 49.

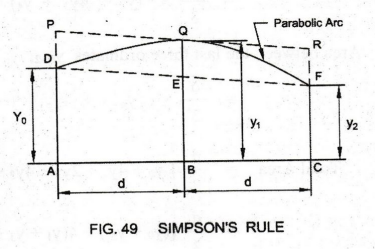
Area between the baseline AC and the vil parabolic arc DQF = (Area of the trapezoid ACFD) + (Area of the segment between the parabolic arc DQF and the corresponding chord DF). Let yo, yı and y2 be the three consecutive ordinates (offsets) drawn at regular intervals of d.

Through Q draw a line PR parallel to the chord DF to cut the ordinates yo and y2 produced at the points P and R.

Simpson's Rule is applicable only if the number of ordinates (offsets) is odd as shown in Fig. 50.

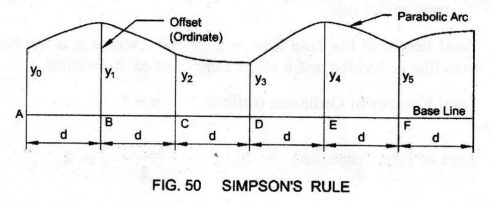
But, if the number of ordinates is even, the area of the last trapezoid is calculated separately and added to the area obtained by Simpson's Rule.

Thus, Simpson's Rule is stated as follows:

Total Area = d/3 [(First Ordinate + Last Ordinate) + 4(Sum of Odd Ordinates) + 2(Sum of Even Ordinates)]

Note

1. If the number of ordinates is even, say, 8, then the area A, for the first seven ordinates only is obtained using Simpson's Rule.

A₁ = d/3 [(y₀ + y₆) + 4(y₁ + y₂ + y₃) + 2(y₂ + y₄)]

and A₂ = Area of Last Trapezoid = 1/2  (y₆ + y₇) d;

Total Area A = A₁ + A₂

2. Interval between ordinates (offsets) should be equal.

3. If yo or yn is equal to zero, that is also included in the Simpson's Rule.

Comparison of Rules

1. Results obtained by Simpson's Rule are more accurate than by Trapezoidal Rule.

2. Results obtained by Simpson's Rule are greater or less than by Trapezoidal Rule, according as the curve of the boundary is concave or convex towards the base line.

PROBLEM 1

The following perpendicular offsets in meters were taken at 10 meter intervals from a survey line to an irregular boundary line: 0, 4, 7, 9, 12, 15, 14, 8 and 3. Determine the area enclosed between the chain line and the boundary line by. (i) Mean Ordinate Rule, (ii) Trapezoidal Rule and (iii) Simpson's Rule. (UQ)

Solution

(i) Area by Mean Ordinate Rule

Area = n / n+1 (y₀ + y₁ + y₂ …… + y_n ) d; In this, Number of Ordinates = 9,

Number of Divisions = n = 8 and Length of each Division = d = 10 m

Sum of all the 9 Ordinates = 0 + 4 + 7 + 9 + 12 + 15 + 14 + 8 + 3 = 72 meters

Area = (8/9) (72 × 10) m² = 640 m²

(ii) Area by Trapezoidal Rule

Area = d [y₀ + y_n / 2 + y₁ + y₂ …… + y_n-1 ]

= 10 [ 0+3 / 2 + 4 + 7 + 9 + 12 + 15+ 14 + 8] m² = 10 × 70.5 m² = 705 m²

(iii) Area by Simpson's Rule: (Number of Ordinates/Offsets is 9, that is Odd.)

Total Area = d/3 (First Ordinate + Last Ordinate) + 4(Sum of Odd Ordinates) + 2(Sum of Even Ordinates)]; In this, d= 10, First Ordinate = 0, Last Ordinate = 3, Odd Ordinates = 4, 9, 15,8 and Even Ordinates = 7, 12, 14.

Total Area = 10/3 [(0 + 3) + 4(4 + 9 + 15 + 8) + 2(7 + 12 + 14)] m²

= 10/3 [3 + 4(36) + 2(33)] m² = 710 m²

PROBLEM 2

The following series of perpendicular offsets were taken from a chain line to a curved boundary line at 5 meter intervals: 0, 3.25, 4.10, 6.45, 8.90, 5.75, 8.50 and 0. Determine the area enclosed between the survey line and the boundary line by (i) Trapezoidal Rule and (ii) Simpson's Rule. (UQ)

Solution

(i) Area by Trapezoidal Rule

Area = d [ y₀ + y _n / 2 + y₁ + y₂ + …. + y_n-1]

In this, d = 5 m, Number of Ordinates = 8, Number of Divisions = n = 7,

Area = 5 [ 0 + 0 / 2 + 3.25 +4.10 + 6.45 + 8.90 +5.75 + 8.50 ]

= 5 [ 0 + 0 / 2 + 3.25 + 4.10 + 6.45 + 8.90 + 5.75 + 8.50]

= 5 × 36.95 = 184.75 m²

(ii) Area by Simpson's Rule

Number of Ordinates/Offsets is 8, i.e., Even. Simpson's Rule can be applied, only if the number of ordinates is odd. Therefore, in this problem, the last ordinate/offset (0) is ignored to calculate the area A₁. Then, the area A₂ of the trapezium between the last two ordinates is calculated.

PROBLEM 3

The following perpendicular offsets were taken at 10 meters intervals from a survey line to an irregular boundary line:

3.25, 5.60, 4.20, 6.65, 8.75, 6.20, 3.25, 4.20 and 5.65.

Calculate the area enclosed between the survey line, the irregular boundary line and the first and last offsets, by the application of (i) Average Ordinate Rule, (ii) Trapezoidal Rule and (iii) Simpson's Rule. (UQ)

Results

(i) Average Ordinate Rule: 424.44 sq m = 4.2444 ares.

(ii) Trapezoidal Rule : 433 sq m = 4.33 ares.

(iii) Simpson's Rule : 439.67 sq m = 4.3967 ares.

PROBLEM 4

A series of offsets were taken from a chain line to a curved boundary line at intervals of 15 meters in the following order:

0, 2.65, 3.80, 3.75, 4.65, 3.60, 4.95 and 5.85.

Compute the area between the chain line, the curved boundary and the end offsets by (i) Average Ordinate Rule, (ii) Trapezoidal Rule and (iii) Simpson's Rule. (UR)

Results

(i) Average Ordinate Rule: 383.91 sq m

(ii) Trapezoidal Rule : 394.87 sq m

(iii) Simpson's Rule : 309.25 + 81.0 = 3.8391 ares. = 3.9487 ares. = 390.25 sq m

= 3.9025 ares.