Capacitance of a Co-axial Cable

Capacitance of a Co-axial Cable

AU : May-05, 14, Dec.-03, 06, 08

• Consider a co-axial cable or co-axial capacitor as shown in the Fig. 5.14.1.

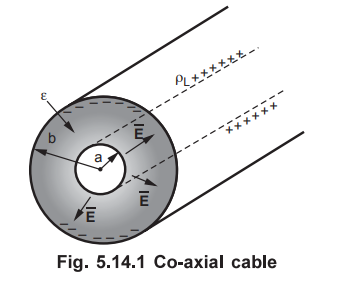
 Let a = Inner radius, b = Outer radius

• The two concentric conductors are separated by dielectric of permittivity Ɛ.

• The length of the cable is L m.

• The inner conductor carries a charge density + ρL C/m on its surface then equal and opposite charge density - ρL C/m exists on the outer conductor.

Q = ρL × L

• Assuming cylindrical co-ordinate system,   will be radial from inner to outer conductor, and for infinite line charge it is given by,

•   is directed from inner conductor to the outer conductor. The potential difference is work done in moving unit charge against   i.e. from r = b to r = a.

• To find potential difference, consider  in radial direction which is dr 

Ex. 5.14.1 Determine the capacitance of concentric cylinders with mixed dielectrics.

AU : Dec.-08, Marks 8

Sol. : Consider the concentric cylinders with different dielectrics as shown in the Fig. 5.14.2. The dielectric interface is parallel to the   hence the configuration can be treated as two capacitors in parallel. Each dielectric occupies one half of the space between the cylinders hence carries half as much charge as a full cylinder would carry. Hence from the result of capacitance of co-axial cable,

Ex. 5.14.2 Conducting cylinders at p = 2 cm and p = 6 cm are at potentials of 100 V and 0 V respectively. The region between the cylinders is filled with an inhomogeneous perfect dielectric for which ƐR = 0.3 /( ρ + 0.04).

Find i) D(ρ) ii) E(ρ) iii) V(ρ) iv) Capacitance per metre length.

Sol . :

Let ρL be the charge density on the inner cylinder. Assuming infinite length, the electric field intensity due to it is given by,

Examples for Practice

Ex. 5.14.3 Find the capacitance of a 20 cm co-axial cable having an inner conductor with 0.0295 inches diameter and an outer conductor with inside diameter of 0.116 inches and a polyethylene dielectric with Ɛr = 2.26.

[Ans.: 18.365 pF]

Review Question

1. Derive the electric field and potential distribution and the capacitance per unit length of a co-axial cable.

AU : Dec.-03, 06, Marks 16