Classical free electron (cfe) theory of metals

CLASSICAL FREE ELECTRON (CFE) THEORY OF METALS

The classical free electron theory of metals was proposed by P. Drude in the year 1900 to explain the electrical conduction in metal. This theory was further extended by H. A. Lorentz in the year 1909.

We know that an atom consists of a central nucleus with positively charged protons surrounded by the electrons of negative charge.

The electrons in the inner shells are called core electrons and those in the outermost shell are called valence electrons (Fig. 2.1).

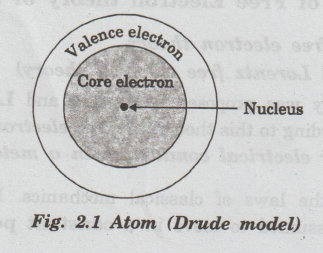
In a metal, when the valence electrons of each atom detach from the orbit, then they move freely throughout the metal. These electrons are known as free or conduction electrons.

Postulates of classical free electron theory

1. According to this theory, a metal consists of very large number of free electrons. These electrons move freely throughout the volume of the metal. The movement of the free electrons is mainly ano responsible for the electrical conduction in the metal.

2. Drude assumed that the free electrons in the metal form an electron gas. They move randomly in all possible directions just like the gas molecules move in a container.

The arrangement of atoms in a metal is viewed as an array of atoms (ions) surrounded by a gas of free electrons. Here, the mutual repulsion between the electrons is neglected. (Fig. 2.2)

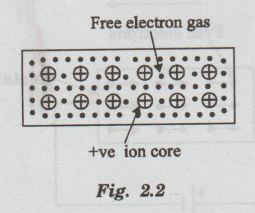
3. In absence of an electrical field, the free electrons (electron gas) move in all directions in a random manner.

They collide with other free electrons and positive. ion core during the motion. This collision is known as elastic collision (Fig 2.3).

As the motion is random, the resultant velocity in any particular direction is zero.

4. When the electrical field is applied the electrons get some amount of energy. These electrons begin to move towards the positive potential (in opposite direction to the applied electrical field).

They continue to collide with positive ion cores fixed bein the lattice. As a result, the free electrons acquire a constant average velocity known as drift velocity ass (Fig. 2.4).

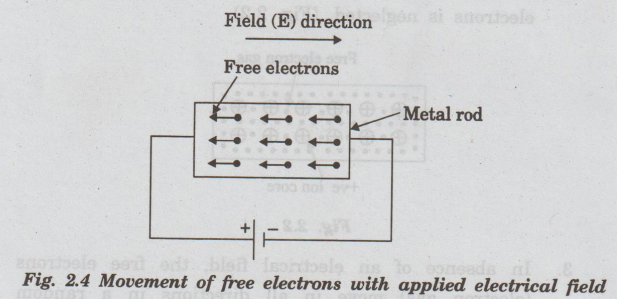
5. The velocity and the energy distribution of free electrons are governed by classical Maxwell distribution function.

6. Since the electrons are assumed to be a perfect gas, they obey the laws of kinetic theory of gases.

Therefore, the free electrons are assigned with mean free path, mean collision time and average velocity.

Drift velocity (v_d)

It is defined as the average velocity acquired by the free electrons of a metal in a particular direction by the application of an electrical field.

It is expressed as

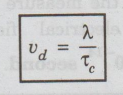
where λ  - mean free path

τc -  collision time.

Mean free path (λ)

The average distance travelled by a free electron between any two successive collisions is known as mean free path. It is represented by λ.

It is the product of drift velocity of free electrons (v_d) and collision time (τ_c).

λ = v_d τ_c

Collision time (τ_c)

The average time taken by a free electron between any two successive collisions is known as collision time of the electron.

It means that the electron on an average travels for a time τ before its next collision.

It is given by

τ_{c  =} λ / V_d

where λ - mean free path

V_d - drift velocity

Relaxation time (τ)

The average time taken by a free electron to reach its equilibrium state from its disturbed state due to the application of an external electrical field is called relaxation time.

In other words, it is the measure of time that the electrons relax when the electrical field is the electrical field is removed. It is approximately equal to 10^-14 second.

For isotropic material such as metal collision time (τ_c) = relaxation time (τ).