Code Converters

Code Converters

AU : Dec.-03, 11, 14, 15, 16, June-09, Hay-10, 11, 15, 16

• There is a wide variety of binary codes used in digital systems. Some of these codes are Binary-Coded-Decimal (BCD), Excess-3, Gray and so on. Many times it is required to convert one code to another.

• Let us see the procedure to design code converters :

Step 1 : Write the truth table showing the relationship between input code and output code.

Step 2 : For each output code bit determine the simplified Boolean expression using K-map.

Step 3 : Realize the code converter using logic gates.

Examples for Understanding

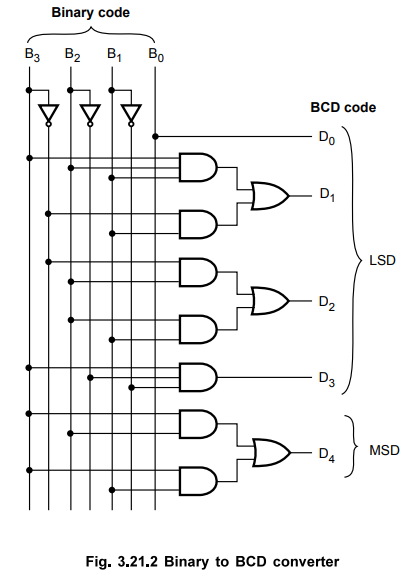
Ex. 3.21.1 Design a 4-bit binary to BCD converter.

Step 1 : Form the truth table relating binary and BCD code.

Input code : Binary code : B₃ B₂ B₁ B₀ (B₀ LSB)

Output code : BCD (Decimal) code : D₄ D₃ D₂ D₁ D₀ (D₀ LSB)

Step 2 : K-map simplification for each BCD output

Step 3 : Realization of code converter

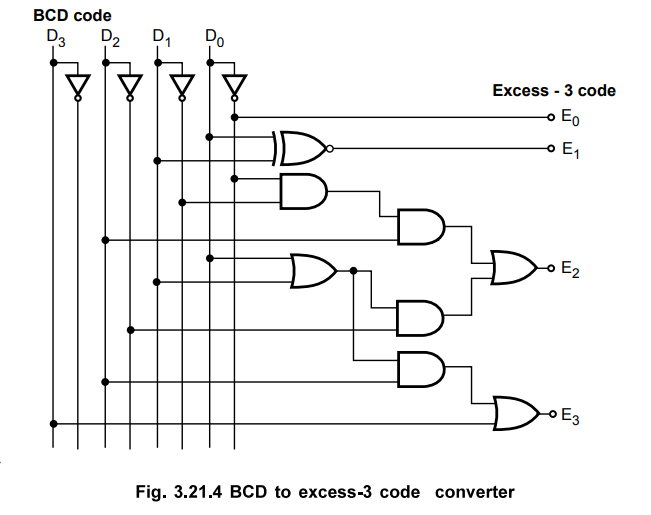
Ex. 3.21.2 Design a logic circuit to convert the 8421 BCD to Excess-3 code.

Sol. :

Step 1 : Form the truth table relating BCD and Excess-3 code.

Excess-3 code is a modified form of a BCD number. The Excess-3 code can be derived from the natural BCD code by adding 3 to each coded number. For example, decimal 12 can be represented in BCD as 0001 0010. Now adding 3 to each digit we get Excess-3 code as 0100 0101 (12 in decimal). With this information the truth table for BCD to Excess-3 code converter can be determined as shown in Table 3.21.2.

Input code : BCD code : D₃ D₂ D₁ D₀ (D₀ LSB)

Output code : Excess-3 code : E₃ E₂ E₁ E₀ (E₀ LSB)

Step 2 : K-map simplification for each Excess-3 code output.

Step 3 : Realization of code converter.

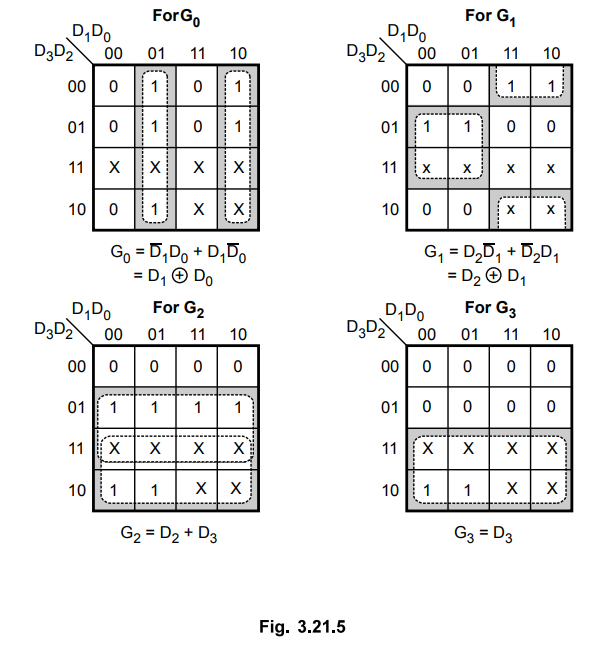
Ex. 3.21.3 Design a logic circuit to convert BCD to gray code.

Solution :

Step 1 : Form the truth table relating BCD and gray code.

Input code : BCD code : D₃ D₂ D₁ D₀ (D₀ LSB)

Output code : Gray code : G₃ G₂ G₁ G₀ (G₀ LSB)

Table 3.21.3 shows truth table for BCD to gray code converter.

Step 2 : K-map simplification

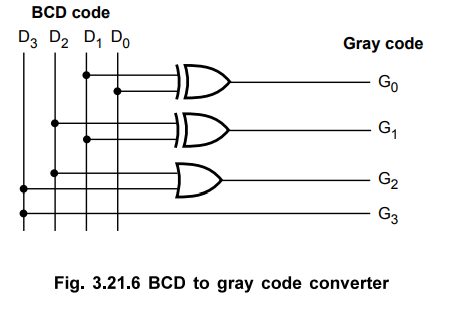
Step 3 : Realization of code converter.

Ex. 3.21.4 Design and implement a 8421 to Gray code converter. Realize the converter using only NAND gates.

AU : June-09, Marks 16, Dec.-14, 16, Marks 8

Sol. :

Step 1 : Form the Truth table relating 8421 binary code and BCD code

Input code : Binary code : B₃ B₂ B₁ B₀

Output code : Gray code : G₃ G₂ G₁ G₀

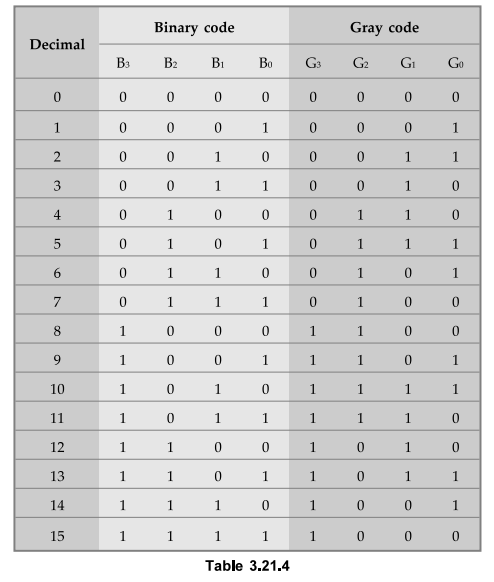
Step 2 : K-map simplification for each gray code output

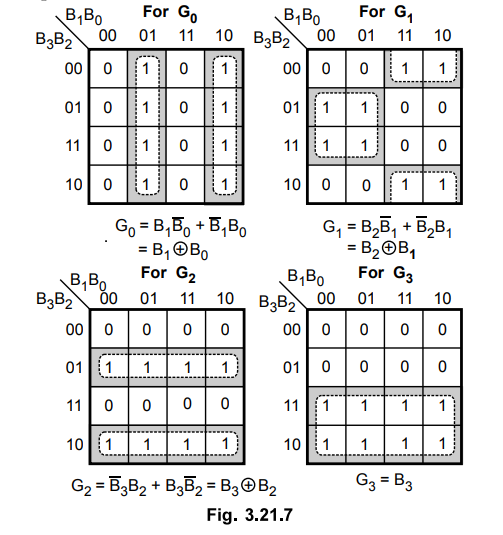
Step 3 : Realization of code converter using XOR-gates

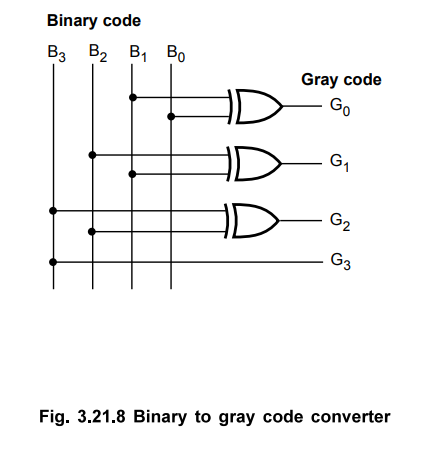
Step 4 : Realization of code converter using NAND gates

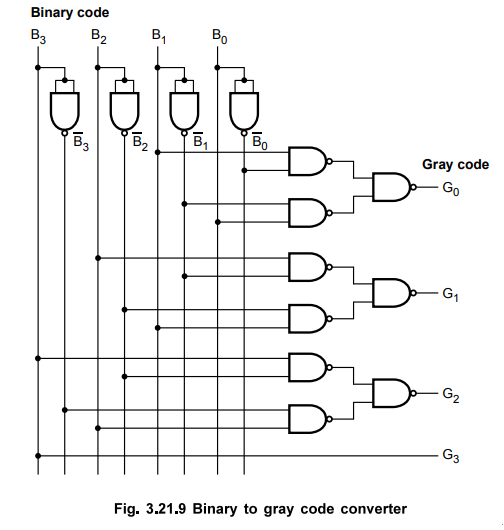
 For this converter we have derived the Boolean expressions for each gray code output in the Sum Of Product (SOP) form. We can implement SOP expression using AND-OR logic or NAND-NAND logic. Let us see the implementation of code converter using NAND-NAND logic.

Examples for Practice

Ex. 3.21.5 Design a logic circuit to convert excess-3 code to BCD code.

Ex. 3.21.6 Design a logic circuit to convert gray code to binary code.

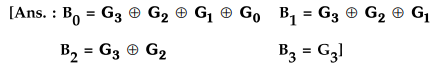
Review Question

1. Write brief note on binary to gray code converter.

AU : Dec.-11, Marks 4