Comparison of Conductor Material in Overhead System

Comparison of Conductor Material in Overhead System

AU : May-07, 13, Dec.-08

The selection of a particular type of a.c. or d.c. system for the transmission and distribution is based on comparison of amount of material i.e. copper necessary for the various systems. As mentioned earlier, the maximum stress in the overhead system exists between the conductor and earth. Hence comparison of material required is done assuming the maximum voltage between any conductor and earth being the same. The assumptions made for the comparison are :

1. The power (P) transmitted by all the systems is same.

2. The distance (l) over which the power is transmitted is same.

3. The power losses (W) in all the systems are same.

4. The maximum voltage (V_m) exists between any conductor and the earth, in all the systems.

Based on these assumptions, let us compare the various types of systems for the volume of copper required.

 

1. Two Wire D.C. System with One Line Earthed

The system is represented in the Fig. 7.16.1.

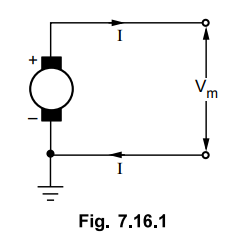
The maximum voltage between the conductors is Vm, as one terminal is earthed.

The volume of copper required for other systems is compared by taking volume of copper required for this system as base. Let it be constant K and volume of copper required for other systems can be expressed interms of K.

 

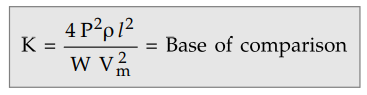
2. Two Wire D.C. System with Midpoint Earthed

The system is represented in the Fig. 7.16.2.

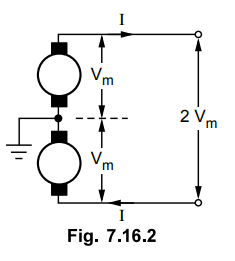
As power transmitted is same as P, the current in each conductor is,

I = P / 2V m

The total copper loss in both the lines is,

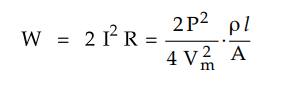
where A = Area of cross-section of each line

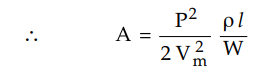
The total volume of copper required is,

Key Point Thus the volume of copper required in this system is one fourth the volume of copper required for two wire d.c. system with one line earthed.

 

3. Three Wire D.C. System

The system is represented as shown in the Fig. 7.16.3.

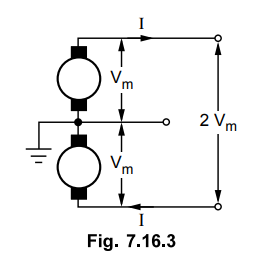
When the load is balanced, current through the third neutral wire is zero.

I = P / 2V_m

Let A = cross-section of outer conductors

The total copper loss is,

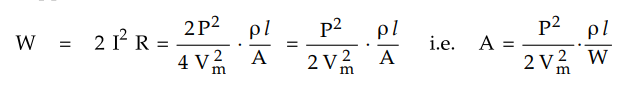
Let area of cross-section of the middle neutral wire is half of the area of cross-section of the outer conductor.

Hence the total volume of copper

= Volume of copper for outer wires + Volume of copper for neutral wire

Key Point Thus the volume of copper required in this system is 0.3125 times the volume of copper required for two wire d.c. system with one line earthed.

 

4. Two Wire Single Phase A.C. System with One Conductor Earthed

The system is represented in the Fig. 7.16.4. 

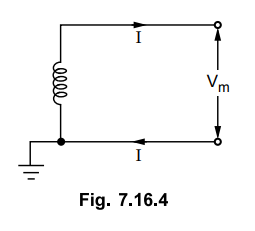
The maximum voltage between the conductors is V_m as one terminal is earthed and the r.m.s. value of voltage is V_m / √2. Let the power factor (p.f.) of the load be cos ϕ. Let the total power transmitted be P watts.

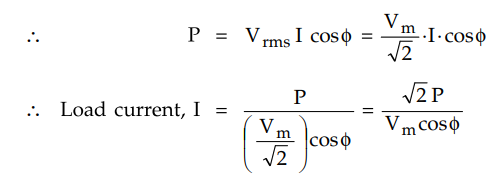
Let R be resistance of each conductor, then R = ρl / A

Here A is area of cross-section of conductor.

Total copper losses in both the conductors are,

Key Point Thus the volume of copper required in this system is1/cos²ϕ times the volume of copper required for two wire d.c. system with one conductor earthed.

 

5. Two Wire Single Phase A.C. System with Midpoint Earthed

The system is represented in the Fig. 7.16.5. 

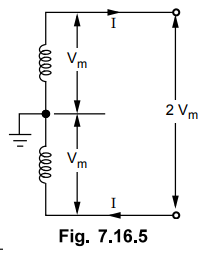
The voltage of the two wires with respect to earth is Vm. The voltage between the two wires is 2 Vm and its r.m.s. value is 2V_m / √2 = √2 V_m. Let the p.f. of load be cos ϕ.

Let the power transmitted be P watts. 

Thus the volume of copper required in this system is 1 / cos²ϕ times the volume of copper required for two wire d.c. system with one conductor earthed.

 

6. Three Wire Single Phase A.C. System

The system is represented in the Fig. 7.16.6. This system is similar to 3 wire d.c. system in principle.

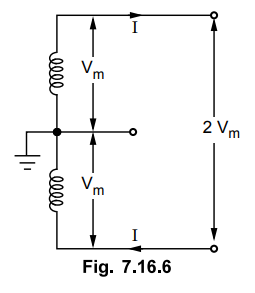
It consists of two outer wires and one neutral wire taken from the midpoint of the phase winding.

If the load is assumed to be balanced then the current in neutral will be zero. Let us consider this case.

Voltage between conductors = 2 Vm

R.M.S. value of voltage = 2 V_m / √2 = √2 V_m

Let the p.f. of load be cos ϕ and total power transmitted be P watts.

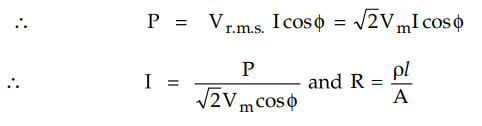
Total copper losses in both the conductors are,

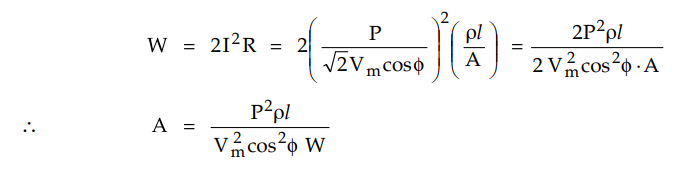
Let the area of cross-section of the middle neutral wire is half of the area of cross section of the outer conductor.

Hence total volume of copper required is given by,

Key Point Thus the volume of copper required in this system is 5/8cos² ϕ of times the volume of copper required for two wire d.c. system with one conductor earthed.

 

7. Three Wire Two Phase A.C. System

The system is represented as shown in Fig. 7.16.7. The voltages of the two windings are in quadrature with each other. From the junction of two phase windings, the neutral wire is taken. The total power transmitted gets divided equally between the two windings and each transmits one half of total power.

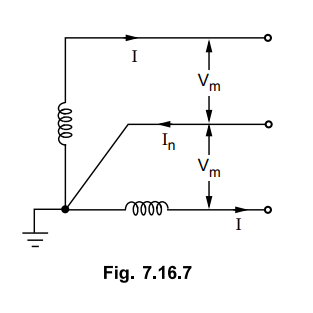
Let V_m be maximum voltage of any one winding with respect to neutral while its r.m.s. value is V_m / √2.

Let the p.f. of load be cos 4 and power transmitted by each outgoing conductor is P/2 where P is total power transmitted.

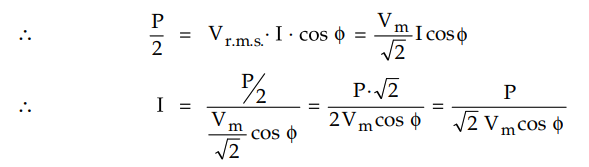
The current in neutral wire is the phasor sum of currents in outer wires. The currents are 90° apart (or in quadrature) from each other. The magnitude of the current in neutral wire is given as,

I_n = √I² + I² = √2.I

As the current in neutral wire is √2 times more than current in other conductors, the cross-section of neutral conductor must be increased by √2 to have same current density.

Resistance of neutral wire,

R_n = ρl / A_n

But as its cross-section is increased, its resistance is given as,

Here A is area of outer conductors and its resistance is,

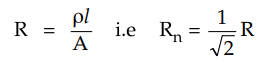
Total copper losses are given by,

W = Copper losses in outer conductors + Copper losses in neutral conductor

Key Point Thus the volume of copper required in this system is 1.457/cos² ϕ times the volume of copper required for two wire d.c. system with one conductor earthed.

 

8. Four Wire Two Phase A.C. System

The system is represented in the Fig. 7.16.8. The midpoints of the two windings are joined together. From the ends of two phase windings, four wires are taken.

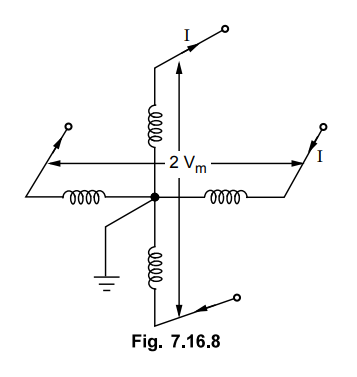
This system is equivalent to two independent single phase systems with each system transmitting half of total power.

Let V_m be maximum voltage of any one winding with respect to earth and voltage between conductors is 2V_m . The r.m.s. value of voltage is 2V_m / √ 2 = √2Vm.

Let p.f. of load be cos 0 and power supplied by each outgoing conductor is P/2. We have,

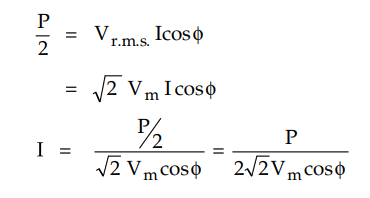
Let R be resistance of each conductor such that R = ρl / A where A is area of cross-section of conductor.

 

9. Three Phase Three Wire A.C. System

This is most commonly used system for the transmission. The three phase three wire star connected system with neutral earthed is shown in the Fig. 7.16.9.

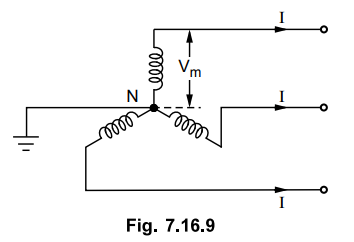
The maximum voltage between each line conductor and the neutral is V_m as shown in the Fig. 7.16.9.

The r.m.s. value of the voltage per phase is given by,

Vph = V_m / √2

The total power transmitted is P watts hence per phase power transmission is,

P_ph = P/3

Let cos ϕ be the load power factor

Key Point Thus the volume of copper required, depends on power factor of the load and it is 0.5/cos²ϕ times the volume of copper required bp two wire d.c. system with one line earthed. This system may be delta connected but irrespective of the method of connection star or delta, the result derived remains same. 

 

10. Three Phase Four Wire A.C. System

This system is popularly used for secondary distribution. The neutral is also made available for the connection of the load. The system is shown in the Fig. 7.16.10.

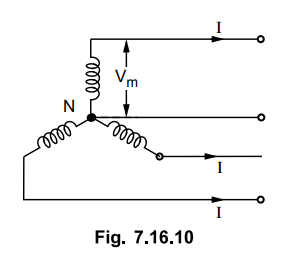
Assuming the load balanced, there is no current flowing through the neutral.

The cross-section area of neutral is half the cross-section of each conductor i.e. 0.5 A where A is cross-section of each conductor.

The maximum voltage between any conductor and voltage per phase is,

V_ph = Vm / √2

The power transmitted per phase is,

V_ph = P / 3

Hence all the calculations upto the copper losses and expression of A remain same as derived for three phase three wire system.

Key Point Thus the volume of copper required is 0.583/cos² ϕ times the volume of copper required by two wire d.c. system with one line earthed.

 

Example 7.16.1 A 50 km long transmission line supplies a load of 5 MV A at 0.8 p.f. lagging at 33 kV. The efficiency of transmission is 90 %. Calculate the volume of aluminium conductor required for the line when i) single phase, 2-wire system is used ii) 3-phase, 3 wire system is used. The specific resistance of aluminimum is 2.85 × 10^-8 Ω m.

Solution :  

Review Questions

1. Calculate the volume of the conductor material required for 1-ϕ, 2 wire a.c. system with one conductor earthed for overhead transmission system.

2. Prove that the volume cf copper material required by three phase three wire system is 0.5 / cos²ϕ times the volume of copper required by two wire d.c. system, irrespective of whether system is star or delta connected, in overhead type of transmission.

3. Compare the various overhead a.c. and d.c. systems based on the volume of copper required. State the assumptions used.

4. Find the ratio of volume of copper required to transmit a given power over a given distance by overhead system using :

i) D.C. 2 wire and 3 wire system, ii) 3ϕ, 3 wire AC system.