Composite Parallel Plate Capacitor (Mixed Dielectrics)

Composite Parallel Plate Capacitor (Mixed Dielectrics)

AU : May-05, 10, 18, Dec.-13, 16, 17

• The composite parallel plate capacitor is one in which the space between the plates is filled with more than one dielectric. Consider a composite capacitor with space filled with two separate dielectrics for the distances d₁ and d₂.

• This is shown in the Fig. 5.16.1. The dielectric interface is parallel to the conducting plates.

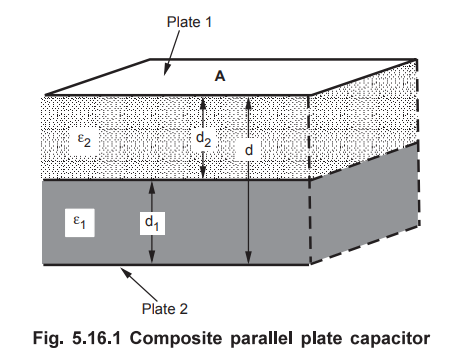
•  The space d₁ is filled with dielectric having permittivity Ɛ₁ while sp ace d₂ is filled with dielectric having permittivity Ɛ₂.

Let Q = Charge on each plate

 = Field intensity in region d₁

 = Field intensity in region d₂

• Both the intensities are uniform.

V₁ = E₁d₁

and    V₂ = E₂d₂

• where E₁ and E₂ are the magnitudes of the two intensities.

V = V₁ + V₂ = E₁d₁ + E₂d₂ ...(5.16.1)

At a dielectric - dielectric interface, the normal components of flux densities are equal i.e.

D_N1 = D_N2

Now  D₁ = Ɛ₁E₁    and    D₂ = Ɛ₂E₂

Substituting in equation (5.16.1),

V = (D₁ / Ɛ₁ ) d₁ + (D₂ / Ɛ₂ ) d₂ (5.16.2)

The magnitude of surface charge is same on each plate hence

ρS = D₁ = D₂ (5.16.3)

Substituting in equation (5.16.2)

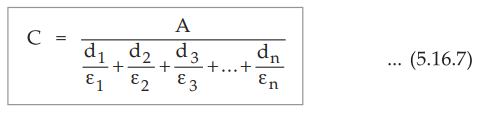
Thus the result can be generalized for a capacitor with n dielectrics as,

1. Dielectric Boundary Normal to the Plates

• Consider the composite capacitor in which dielectric boundary is normal to the conducting plates.

• The dielectric Ɛ₁ occupying area A₁ of the plates while the dielectric Ɛ₂ occupying area A₂, as shown in the Fig. 5.16.2.

• The total potential across the two plates is V and distance between the plates is d. Hence magnitude of  is,

E = V / d … (5.16.8)

• At the boundary, both  are tangential and for dielectric - dielectric interface tangential components are equal.

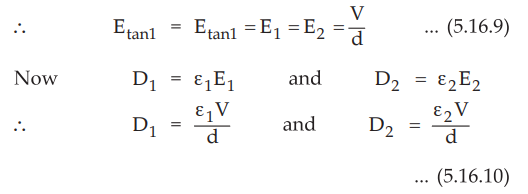
• On the plate the charge is divided into two parts.

• On area A₁, the charge density is ρ_S1 = D₁ while on area A₂, the charge density is ρ_S2 = D₂

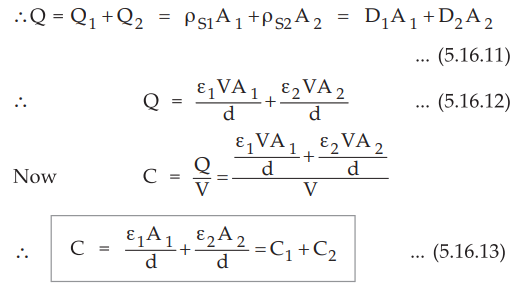
• Thus if dielectric boundary is parallel to the plates, the arrangement is equivalent to two capacitors in series for which While if the dielectric boundary is normal to the plates, the arrangement is equivalent to two capacitors in parallel for which C_eq = C₁ + C₂ |.

Ex. 5.16.1 A parallel plate capacitor with a separation of 1 cm has 29 kV applied, when air was the dielectric used. Assume that the dielectric strength of air as 30 kV/cm. A thin piece of glass with Ɛr = 6.5 with a dielectric strength of 290 kV/cm with thickness 0.2 cm is inserted. Find whether glass will break or air ?

Sol. : The arrangement is shown in the Fig. 5.16.3.

The dielectric strength of air is 30 kV/cm and Eair is more than that hence air will breakdown.

The dielectric strength of glass is 290 kV/cm and E_glass is less than that hence glass will not breakdown.

Ex. 5.16.2 Find the capacitance of a parallel plate capacitor with dielectric Ɛ_r1 = 1.5 and Ɛ_r2 = 3.5 each occupy one half of the space between the plates of area 2 m² and d = 10^-3 m

AU : Dec-16, Marks 7

Sol. :

The arrangement is shown in the Fig. 5.16.4

Ex. 5.16.3 : A parallel plate capacitor has a plate separation t. The capacitance with air only between the plates is C. When a slab of thickness t' and relative permitivity Ɛ' is placed on one of the plates, the capacitance is C show that

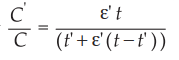
May-18, Marks 7

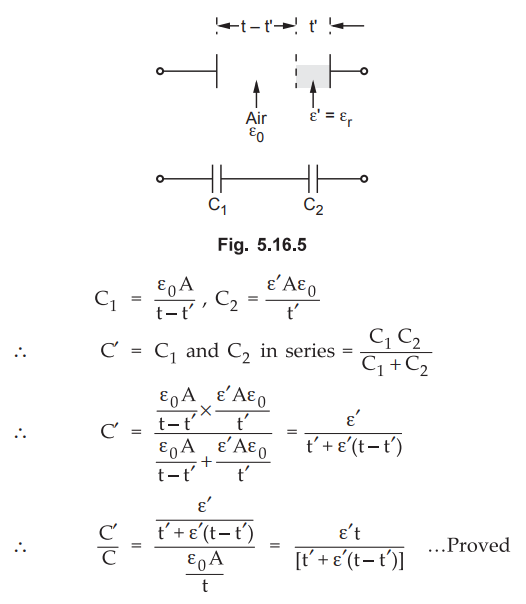
Sol. : With separation t and air as dielectric, the capacitor is,

C = Ɛ₀A / t

Due to slab inserted, the capacitor becomes as shown in the Fig. 5.16.5.

Exampels for Practice

Ex. 5.16.4 Determine the capacitance of each of the capacitors in Fig. 5.16.6. Consider Ɛ_r1  = 4, Ɛ_r2 =6, d = 2 mm, S = 20 cm².

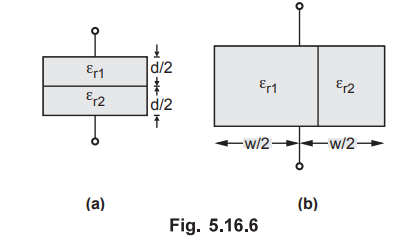
 [Ans.: 42.5 pF, 44.27 pF]

Review Questions

1. Deduce an expression for the capacitance of parallel plate capacitor having two dielectric media.

AU : May-10, 16, Marks 10, Dec.-13, Marks 16

2. Discuss in detail, the electric field in multiple dielectrics.

AU : Dec.-17, Marks 6