Conductors

Conductors

AU : May-08

• Let us study the behaviour and properties of the conductors. Under the effect of applied electric field, the available free electrons start moving. The moving electrons strike the adjacent atoms and rebound in the random directions. This is called drifting of the electrons. After some time, the electrons attain the constant average velocity called drift velocity (vd). The current constituted due to the drifting of such electrons in metallic conductors is called drift current. The drift velocity is directly proportional to the applied electric field.

The constant of proportionality is called mobility of the electrons in a given material and denoted as µe. It is positive for the electrons.

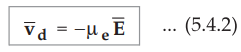
• The negative sign indicates that the velocity of the electrons is against the direction of field .

Now µ(mobility) Velocity / Field = m/s / V/m = m² / V- s

• Thus mobility is measured in square metres per volt-second (m²/V-s). The typical values of mobility are 0.0012 for aluminium, 0.0032 for copper etc.

• According to relation between  we can write,

• But in the material, the number of protons and electrons is same and it is always electrically neutral. Hence ρv = 0 for the neutral materials. The drift velocity is the velocity of free electrons hence the above relation can be expressed as,

where ρe = Charge density due to free electrons

• The charge density ρe can be obtained as the product of number of free electrons/m³ and the charge 'e' on one electron. Thus ρe = ne where n is number of free electrons per m³.

• Substituting equation (5.4.2) in (5.4.4) we get,

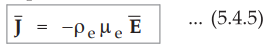
1. Point Form of Ohm’s Law

• The relationship between can also be expressed in terms of conductivity of the material.

• Thus for a metallic conductor,

where σ = Conductivity of the material

• The conductivity is measured in mhos per metre  The equation (5.4.6) is called point form of Ohm's law. The unit of conductivity is also called Siemens per metre (S/m). The typical values of conductivity are 3.82 × 10⁷ for aluminium,

5.8 × 10⁷ for copper etc. expressed in mho/m. For the metallic conductors the conductivity is constant over wide ranges of current density and electric field intensity. In all directions, metallic conductors have same properties hence called isotropic in nature. Such materials obey the Ohm's law very faithfully.

• Comparing the equation (5.4.5) and (5.4.6) we can write,

σ = -ρ_eµ_e …. (5-4.7)

• This is conductivity interms of mobility of the charge density of the electrons.

• The resistivity is the reciprocal of the conductivity. The conductivity depends on the temperature. As the temperature increases, the vibrations of crystalline structure of atoms increases. Due to increased vibrations of electrons, drift velocity decreases, hence the mobility and conductivity decreases. So as temperature increases, the conductivity decreases and resistivity increases.

2. Resistance of a Conductor

• Consider that the voltage V is applied to a conductor of length L having uniform cross-section S, as shown in the Fig. 5.4.1.

• The direction of  is same as the direction of conventional current, which is opposite to the flow of electrons. The electric field applied is uniform and its magnitude is given by,

E = V / L     ... (5.4.8)

• The conductor has uniform cross-section S and hence we can write,

• The current direction is normal to the surface S.

Thus, J = I / S = σ E       ... (5.4.10)

• And using equation (5.4.8) in (5.4.10) we get,

J = σV / L

where  σ = Conductivity of the material ... (5.4.11)

V = JL / σ = IL / σS = (L / σS)r …. (5.4.12)

R = V / I = L / σS …. (5.4.13)

• Thus the ratio of potential difference between the two ends of the conductors to the current flowing through it is resistance of the conductor.

• The equation (5.4.12) is nothing but the Ohm’s law in its normal form given by V = IR. The equation is true for the uniform fields and resistance is measured is ohms (Ω).

• For nonuniform fields, the resistance R is defined as the ratio V to I where V is the potential difference between two specified equipotential surfaces in the material and I is the current crossing the more positive surface of the two, into the material. Mathematically the resistance for nonuniform fields is given by,

• The numerator is a line integration giving potential difference across two ends while the denominator is a surface integration giving current flowing through the material.

• The resistance can also be expressed as,

R = L / σS = (ρcL / S)Ω... (5.4.15)

where ρc = 1/σ = Resistivity of the conductor in Ω -m

3. Properties of Conductor

• Consider that the charge distribution is suddenly unbalanced inside the conductor. There are number of electrons trying to reside inside the conductor. All the electrons are negatively charged and they start repelling each other due to their own electric fields. Such electrons get accelerated away from each other, till all the electrons causing interior imbalance, reach at the surface of the conductor.

• The conductor is surrounded by the insulating medium and hence electrons just driven from the interior of the conductor, reside over the surface. Thus,

1. Under static conditions, no charge and no electric field can exist at any point within the conducting material.

2. The charge can exist on the surface of the conductor giving rise to surface charge density.

3. Within a conductor, the charge density is always zero.

4. The charge distribution on the surface depends on the shape of the surface.

5. The conductivity of an ideal conductor is infinite.

6. The conductor surface is an equipotential surface.

Ex. 5.4.1 An aluminium conductor is 2000 ft long and has a circular cross-section with a diameter of 20 mm. If there is a d.c. voltage of 1.2 V between the ends find : a) The current density b) The current c) Power dissipated from the knowledge of circuit theory. Assume σ = 3.82 × 10⁷ mho/m for aluminium.

Sol . :

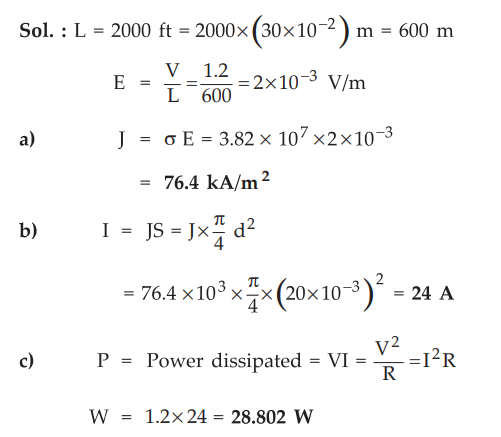
Examples for Practice

Ex. 5.4.2 A wire of diameter 1 mm and conductivity 5 × l0⁷ S/m has 10²⁹ free electrons/m³ when an electric field of 10 mV/m is applied. Determine :

i) The current density

ii) The current in the wire

iii) The charge density of free electrons.

[Ans.: 500 kA/m²,0.3926 A, -1.6 × 10¹⁰ C/m³]

Ex. 5.4.3 A copper conductor having a 0.8 mm diameter and length 2 cm carries a current of 20 A. Find the electric field intensity, the voltage drop and resistance for 2 cm length. Assume conductivity of copper as 5.8 × 10⁷ S/m.

[Ans.: 0.686 V/m, 0.0137 V, 6.86 × 10^-4 Ω]

Review Questions

1. Explain the properties of conductor.

AU : May-08, Marks 4

2. Derive the Ohm's law in point form.

3. Obtain the expression for resistance of a conductor.