Continuity Equation

Continuity Equation

• The continuity equation of the current is based on the principle of conservation of charge. The principle states that,

• The charges can neither be created nor be destroyed.

• Consider a closed surface S with a current density, then the total current I crossing the surface S is then given by,

• The current flows outwards from the closed surface. It has been mentioned earlier that the current means the flow of positive charges. Hence the current I is constituted due to outward flow of positive charges from the closed surface S. According to principle of conservation of charge, there must be decrease of an equal amount of positive charge inside the closed surface. Hence the outward rate of flow of positive charge gets balanced by the rate of decrease of charge inside the closed surface.

Let     Q_i = Charge within the closed surface

dQ_i / dt = Rate of decrease of charge inside the closed surface

• The negative sign indicates decrease in charge.

• Due to principle of conservation of charge, this rate of decrease is same as rate of outward flow of charge, which is a current.

• This is the integral form of the continuity equation of the current.

• The negative sign in the equation indicates outward flow of current from the closed surface. So the equation (5.3.2) is indicating outward flowing current I.

• If the current is entering the volume then

•  The point form of the continuity equation can be obtained from the integral form. Using the divergence theorem, convert the surface integral in integral form to the volume integral.

• For a constant surface, the derivative becomes the partial derivative.

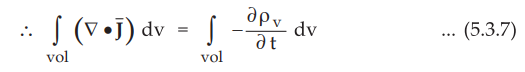
•  If the relation is true for any volume, it must be true even for incremental volume Δv.

• This is the point form or differential form of the continuity equation of the current.

• The equation states that the current or the charge per second, diverging from a small volume per unit volume is equal to the time rate of decrease of charge per unit volume at every point.

1. Steady Current

• For steady currents which are not the functions of time, ∂ρv /∂t = 0 hence,

• For such currents, the rate of flow of charge remains constant with time. The steady currents have no sources or sinks, as it is constant.

• As the area shrinks to a point, the above equation becomes ∑ I at a point = 0. This is nothing but field equivalent of Kirchhoff's current law.

Ex. 5.3.1 Deduce Kirchhoff's current law and Laplace equation from the continuity equation.

AU : Dec.-02, Marks 8

Sol. : The current I crossing the surface S with a current density  is,

Let current flows dutwards from the closed surface. The current means the flow of positive charges. So according to principle of conservation of charge, there must be decrease of an equal amount of positive charge inside the closed surface.

Let Qi = Charge within the closed surface

- dQ_i / dt = Rate of decrease of charge inside the closed surface

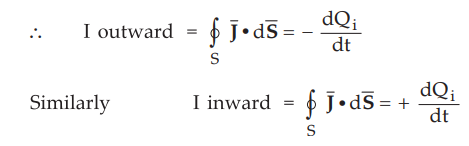
I outward + I inward = dQ_i / dt + dQ_i / dt = 0

This is nothing but Kirchhoff's current law. It can be expressed as,

This states that as much of current must flow into a volume as leaves it.

As the area shrinks to a point, it becomes I = 0. This shows that rate of flow of charge remains constant with time which is nothing but field equivalent of Kirchhoff's current law.

This is nothing but Laplace's equation.

Review Question

1. State and explain the continuity equation in integral and point form.