D.C. Distributor with Concentrated Loads

D.C. Distributor with Concentrated Loads

Dec.-12, May-14, 18

This distributor is further classified as,

1. Fed at one end 2. Fed at both the ends

 

1. Concentrated Loads Fed at One End

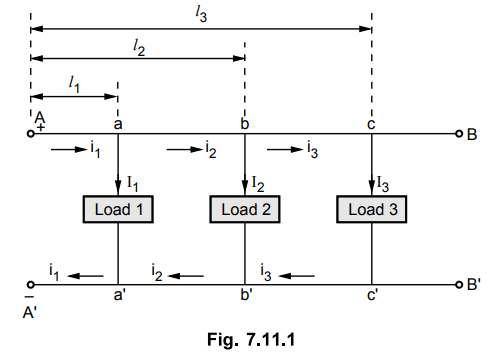
The Fig. 7.11.1 shows a distributor with concentrated loads fed at one end A - A' The loads are connected at the points a - a ', b - b' and c - c'.

Let l₁ , l₂ and l₃ are the lengths of the sections A - a, A - b and A - c respectively. The load currents are I₁, I₂ and I₃. The currents in various sections of the distributor are i₁ i₂ and i₃.

From the Fig. 7.11.1, applying KCL at various points we can write,

i₁ = I₁ + I₂ + I₃, i₂ = I₂ + I₃  and i₃ = I₃

The wire A' B' is the return wire of the distributor.

Let     r' = Resistance per unit length of conductor in Ω

The various voltage drops can be tabulated as,

Applying KVL to any loop, the load point voltages can be calculated.

Now r' is the resistance of single conductor per unit length. And it can be seen that the drops in forward and return conductors are required to be calculated separately and are equal. In practice, the resistance of go and return conductors per unit length is assumed to be r = 2r' and hence two wire distributor can be represented as single wire for calculation purpose, as shown in the Fig. 7.11.2.

And hence all the drop calculations and load point voltages remain same as before. 

The total drop in the distributor is

= r₁ i₁ l₁ + r₂ i₂ l₂ (l₂ – l₁ ) + r₃ i₃ (l₃ – l₂ )

Many times instead of specifying resistances per unit length, actual resistances are specified. The resistance values are of both go and return conductors.

The current loading and voltage drop diagrams are shown in the Fig. 7.11.3.

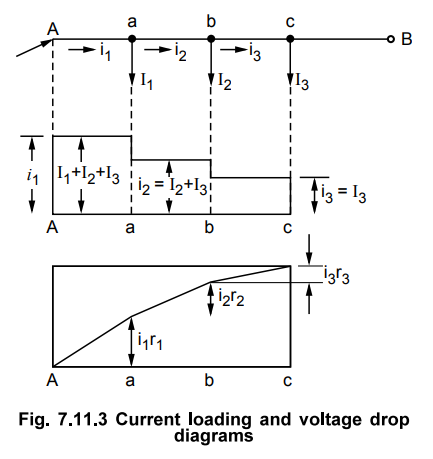
Key Point It can be seen that the minimum potential will occur at point c which is farthest from the point A where the distributor is fed at.

 

2. Concentrated Loads Fed at Both Ends

This type is further classified depending upon the voltage levels at the two ends. 

1. Ends fed with equal voltages and 2. Ends fed with unequal voltages

a. Ends at Equal Voltages

The Fig. 7.11.4 shows this type of distributor. The ends A and B are maintained at equal voltages.

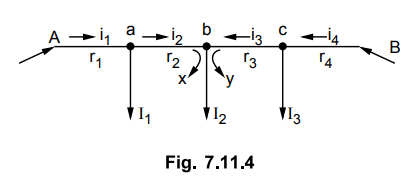
Let r₁, r₂, r₃ and r₄ are the go and return resistances of the sections Aa, ab, bc and cB respectively.

Let point 'b' be the point of minimum potential.

As we move from point A towards B the potential goes on decreasing and at point b becomes minimum. All the currents between section Ab are supplied by point A. After b the voltage goes on increasing till it becomes feeding voltage at B. All the currents between Band b are supplied by the point B.

Now the current at minimum potential point b is supplied by both. Let x be supplied by point A while y be supplied by point B. It is obvious that y = I₂  - x.

As both the points A and B are maintained at same voltage, drop in section Aa must be equal to drop in section Bb.

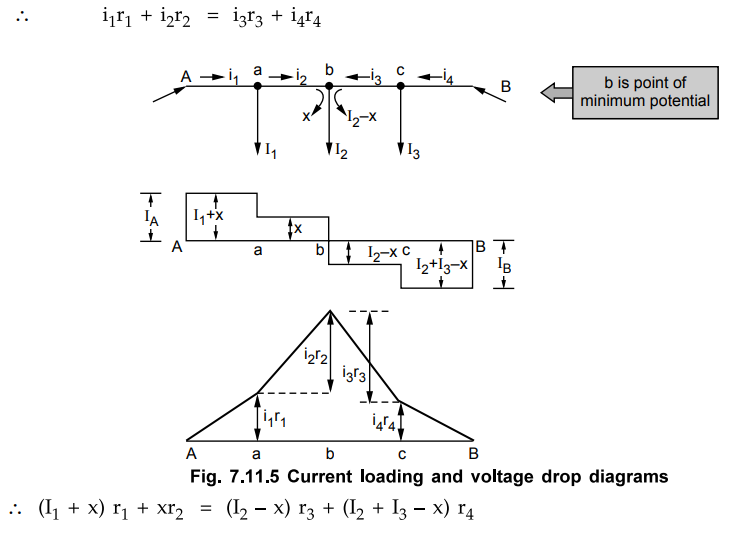
Thus knowing all the currents, x can be calculated and all the voltage drops can be obtained.

The Fig. 7.11.5 shows the current loading and voltage drop diagrams.

Key Point The load point where the currents are coming from both the sides of the distributor is the point of minimum potential.

b. Ends at Unequal Voltages

The Fig. 7.11.6 shows this type of distributor. The ends A and B are maintained at different voltages.

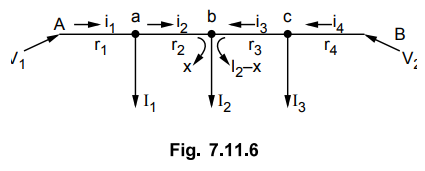
Let the resistances of the sections Aa, ab, bc and cB are r1, 12, 13 and 14 respectively. Let point 'b' is the point of minimum potential.

In this case also the point b is fed by both the points A and B. The current from point A is x while from B it is I₂ - x. Now we can write the equation as,

Voltage drop between A and B = Voltage drop over AB

If voltage of A is V₁ and is greater than voltage of B which is V₂ then,

 V₁ - V₂ = Drops in all the sections of AB

The same equation can be written as,

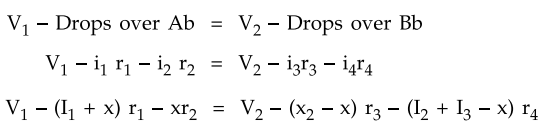
Solving this equation, as V₁ and V₂ are known, x can be obtained.

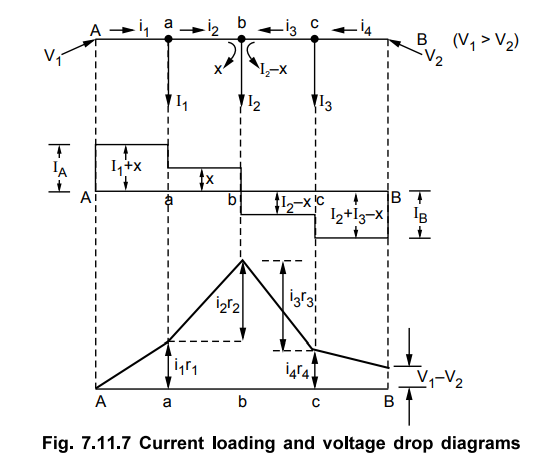
The Fig. 7.11.7 shows the current loading and voltage drop diagrams.

 

Example 7.11.1 A two wire d.c. distributor system is 3 km long and it supplies loads of 200 A, 100 A, 75 A and 50 A at 800 m, 1200 m, 2000 m and 3000 m from the feeding point A. Each conductor has go and return resistance of 0.004 Ω per 100 m. Calculate the voltage at each load point if voltage at feeding point is 250 V.

Solution : The distributor is shown in the Fig. 7.11.8.

These are the voltage at the various load points a, b, c and B.

 

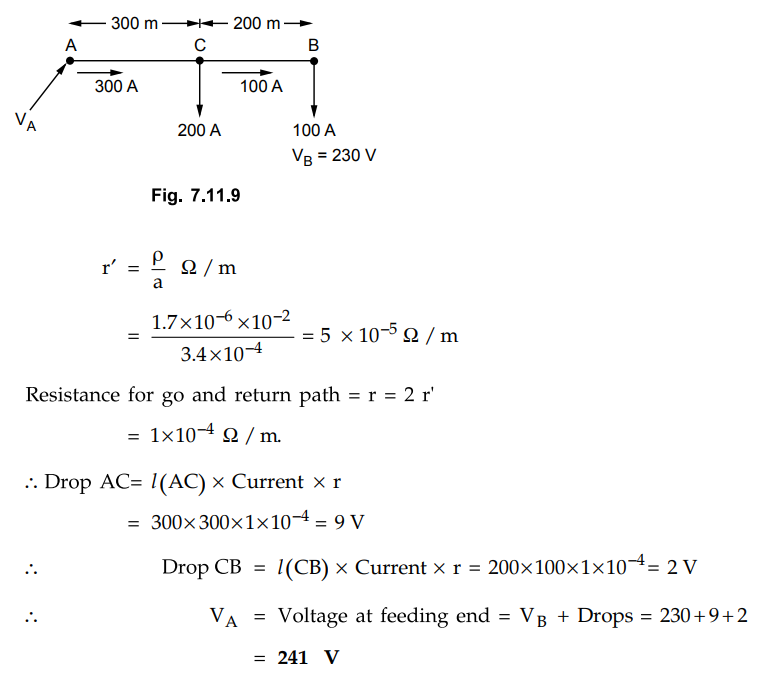
Example 7.11.2 A two wire D.C. distributor 500 m long is fed at one end. The cross sectional area of each conductor is 3.4 cm and resistivity of copper is 1.7 pcm. The distributor supplies 200 A at distance of 300 m from the feeding point and 100 A at the terminal. Calculate the voltage at the feeding end if the voltage at the terminal is to be 230 V.

Solution : The distributor is shown in the Fig. 7.11.9.

 

Example 7.11.3 A two conductor distributor has a length of 700 m and is loaded as shown in Fig. 7.11.10, the distance being represented in meters. The ends A and B are maintained at 250 V and 255 V respectively. If the minimum potential allowable at consumer's terminal is 245 V, calculate the diameter of the conductor used. Resistivity is 1.7 micro ohm-cm.

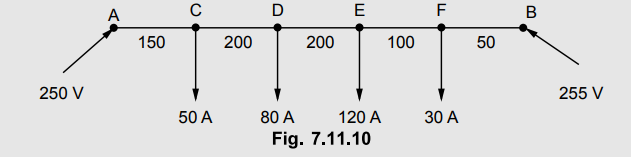
Solution : The distributor is shown in the Fig. 7.11.10 (a). Let r be the resistance for the both go and return per unit    length. Let D be the point of minimum potential. So current of x A is supplied from point A while 80 - x is supplied from point E as shown in the Fig. 7.11.10 (a).

The current distribution is as shown in the Fig. 7.11.10 (b).

The    allowable voltage is 245 V hencemaximum permissible 250 Vvoltage drop is 250 - 245 = 5 V at D from A which is point of minimum potential.

 

Example 7.11.4 Four lines A, B, C and D are connected to a common point O. Resistances of AO, BO, CO and DO are respectively 1, 2, 3 and 4 Ω both go and return and feeding points A, B, C and D are maintained at 230, 250, 240 and 220 V respectively. Find the potential of common point O assuming no load is tapped from there.

Solution : The arrangement is shown in the Fig. 7.11.11.

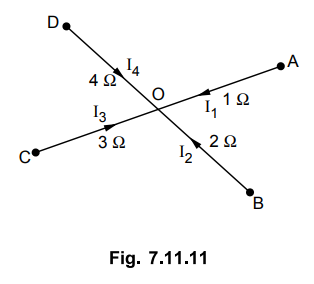
Applying KCL at node O,

where V_O is voltage of point O and no load is tapped from O so summation of all currents entering is zero, no current going away from O. Substituting values V_A, V_B, V_C and V_D we get,

 

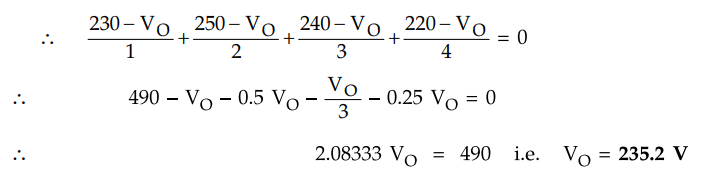
Example 7.11.5 A 2 wire distributor AB is fed at A and supplies six concentrated loads each of 50 A at C, D, E, F, G and H as shown in the Fig. 7.11.12. What must be the resistance of each section so that maximum voltage drop for any consumer does not exceed 7 V ? Also calculate the total power loss with this resistance. Assume that the loads are spaced at equal distances.

Solution : The various currents are shown in the Fig. 7.11.12 (a).

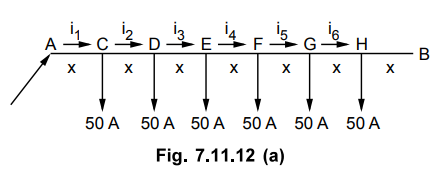
And let x be the resistance of each section of conductor. 

As the loads are equispaced, l(AC) = l (CD) = l (DE) = l (EF) = l (FG) = l (GH)

Hence resistances of all the sections are equal.

Now, i₆ = 50 A     ... no current after H

I₅ = 50 + 50 = 100 A

I₄ = 100 + 50 = 150 A  and  i₃ = 150 + 50 = 200 A

I₂ = 200 + 50 = 250 A  and  i₁ = 250 + 50 = 300 A

The voltage drops in the various sections are i₁x, i₂x, i₃x, i₄x, i₅x, and i₆x

The maximum voltage drop will be at point H which will be the summation of all the drops in the section AC, CD, DE, EF, FG and GH.

 

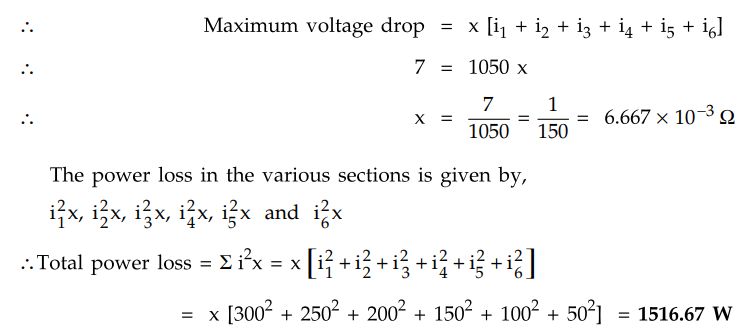
Example 7.11.6 A distributor AF is fed at both ends at the same voltage of 250 V. The length of the distributor is 200 m and the loads are tapped off as follows : 50 A at 50 m from the end A, 50 A at 75 m from A, 30 A at 100 m from A, and 25 A at 150 m from A. Calculate (a) the minimum potential and (b) the voltage at each load point. The resistance per 100 metres of the conductor for go and return is 0.08 Ω.

Solution : Let r be the resistance for both 90 and return per unit length. Let E be the point of minimum potential. Let x amperes be the current supplied at E from B.

Now as two ends are at equal voltages,

Drop (A - E) - Drop (B - E)

 

Example 7.11.7 An electric train taking a constant current of 600 amps moves on a section of line between two substations 8 km apart and maintained at 575 and 590 volts respectively. The track resistance is 0.04 per km both go and return. Find the point of minimum potential along the track and currents supplied by two substations at that instant.

AU : May-14, Marks 8

Solution : The arrangement is shown in the Fig. 7.11.14.

 Let point P be the point of minimum potential at a distance x from A. Let current fed from feeding point A be IA hence current drawn from B is 600 - I_A

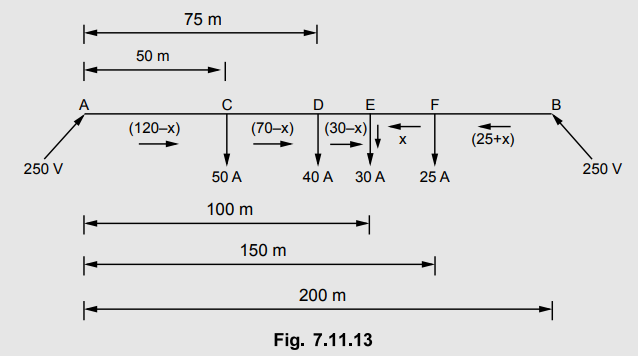
Example 7.11.8 A 2-wire d.c. street mains AB, 600 m long is fed from both ends at 220 V. Loads of 20 A, 40 A, 50 A and 30 A are tapped at distances of 100 m, 250 m, 400 m and 500 m from the end A respectively. If the area of X-section of distributor conductor is 1 square centimeter, find the minimum consumer voltage. Take ρ = 1.7 × 10-6 ohm-cm.

AU : May-18, Marks 15                                

Solution : Let E be the point of minimum potential. At 'E' let x A is supplied from point A while (50 - x) A is supplied from point B.

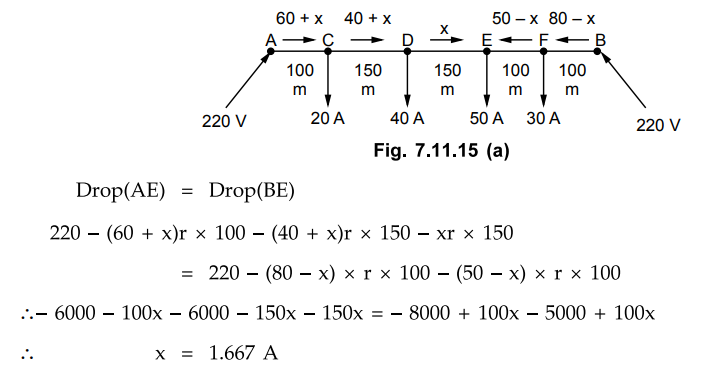
The actual distribution of currents in various sections is shown in the Fig. 7.11.15 (b). 

Review Questions

1. Explain the d.c. distributor fed at one end.

2. Explain the d.c. distributor fed at both ends.

3. Draw and explain the current loading and voltage drop diagrams for :

a. Concentrated loading on distributor fed at one end

b. Concentrated loading on distributor fed at both the ends with equal and unequal voltages.

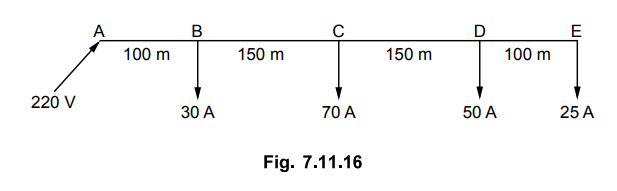
4. A 2 wire distributor 500 m long is loaded as shown in the Fig. 7.11.16. If the maximum voltage drop allowed is 5 % of the supply voltage, calculate the cross-sectional area of the conductor to be used. Take ρ = 1.73× 10^-8 Ω

 [Ans.: 1.667 ×10^-4 m²]

5. A two conductor distributor has a length of 700 m and is loaded as shown in the Fig. 7.11.17. The ends A and B are maintained at 250 and 255 V respectively. If the minimum potential allowable at consumer's terminal is 245 V, calculate the diameter of the conductor used. p = 1.7 μ-cm.

[Ans. : 0.2204 cm]

6. A 2 wire d.c. distributor AB is fed from both ends. At feeding point A the voltage is 230 V while at B it is 235 V. The total length of distributor is 200 m and loads connected are,

25 A at 50 m from A, 50 A at 75 m from A

30 A at 100 m from A, 40 A at 150 m from A

The resistance cf one conductor is 0.3 Ω/km, calculate

a. Currents in various sections b. Point of minimum potential c. Value of minimum potential

[Ans.: Point of minimum potential at 50 A load, 228.875 V]

7. An electric train moves between the substations 8 km apart and draws a constant current of 600 A. The two substations are maintained at a potential of 580 and 575 V respectively. The resistance for both go and return path is 0.05 Ω per km, calculate the minimum potential point and currents supplied by each substation at that instant of minimum potential.

[Ans.: 4.0833 km, 306.25 A, 293.75 A]

8. A 2 wire d.c. ring distributor is fed at A with 220 V. The various loads are 10 A at B, 20 A at C, 30 A at D and 10 A at E. The resistances of the sections AB, BC, DC, DE and EA are 0.1 Ω, 0.05 Ω, 0.01 Ω, 0.025 Ω and 0.075 Ω respectively.

Determine, a. Point of minimum potential b. Current in each section.

[Ans.: Point C, 29.04 A, 19.04 A, 0.96 A, 30.96 A and 40.96 A]