D.C. Three Wire System

D.C. Three Wire System

It is known that higher the voltage level, lower are the transmission losses. But in case of d.c. distribution, level can not be increased readily like a.c. Using rotating machinery, the d.c. voltage level can be increased but the method is too expensive. The d.c. three wire system can be used to double the transmission voltage, without increasing the voltage between either conductor and earth. The higher voltage demand also can be satisfied using d.c. three wire distribution system.

In this system, two generators are connected in series, each is generating a voltage of V volts. The common point is neutral from where neutral wire is rim. The voltage V of each generator is with respect to neutral which is earthed. Thus the voltage between each line and neutral is V volts while between the lines it is 2 V volts. Thus the consumers demanding higher voltage are connected to the two lines while the consumers demanding less voltage for lighting load are connected between any one line and neutral. The Fig. 7.8.1 shows the d.c. three wire distribution system.

The light loads, domestic loads are connected between any of the two lines and neutral while the d.c. motor loads requiring higher voltage are connected between the lines. The neutral is earthed. 

The symbolic representation of three wire d.c. system is shown in the Fig. 7.8.2.

The Fig. 7.8.2 shows the current distribution in the system. The one line carries current I₁ while the other line carries current I₂. When the load is balanced, that is loads connected on either sides of the neutral wire are equal, then the neutral current is zero. And under such condition, the potential of the neutral wire is exactly half of the potential between the two outer lines. Thus the positive outer wire is at V volts above the neutral while the negative outer wire is at V volts below the neutral.

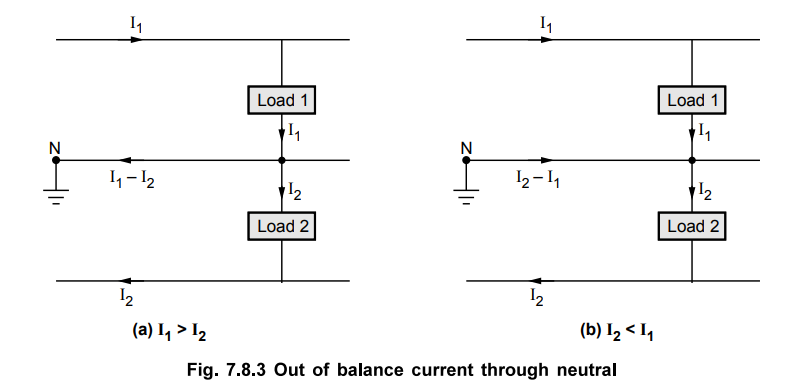
If the loads are not balanced then the neutral carries the current. This current is the difference between the two line currents I₁ and I₂ and is called out of balance current. If the load on the positive line i.e. Ix is greater than I₂ then neutral wire carries current equal to I₁ - I₂. If the load on the negative line is greater i.e. I₂ is greater than Ij then the neutral wire carries current equal to I₂ - Ip This is shown in the Fig. 7.8.3 (a) and (b). The direction of I₁ - I₂ is from load end to supply end while the direction of I₂ – I₁ is from supply end to load end.

In any of the two cases of out of balance current conditions, the neutral potential will not remain half of that between the two lines.

Instead of using two generators in series, a single generator having twice the line to neutral voltage rating also can be used. 

This is shown in the Fig. 7.8.4.

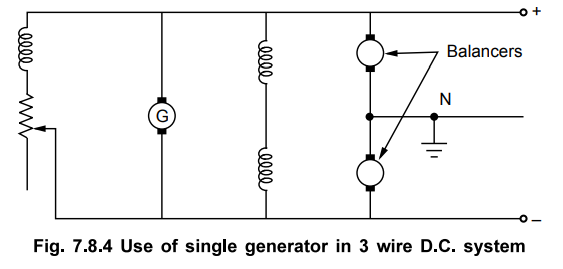
In such system, two small d.c. machines are connected across the lines in series which are mechanically coupled to a common shaft, these are called balancers.

Normally when the load is balanced, machines work as the d.c. motors. In case of any out of balance current through neutral then the machine connected to lightly loaded side acts as motor while that connected to heavily loaded side acts as generator. And the energy is transferred from lightly loaded side to heavily loaded side as machine as motor drives the machine as generator. Thus the imbalance is compensated.

The perfect balancing can not be obtained because the working of the balancers are based on slight unbalancing of the voltages on the two sides.

1. Current Distribution in 3 Wire D.C. System

The Fig. 7.8.5 shows 400/200 V, 3 wire d.c. distribution system. The total current distribution can be understood by taking concrete values of load currents. The motor load connected across the lines demand 175 A while other loads requiring less voltage, are connected between line and neutral, on both the sides of neutral. The two loads connected between positive line and neutral take 35 and 25 A current respectively while the two loads connected between negative line and neutral take 50 A current each.

Applying Kirchhoff's current law at various nodes, the currents in all the sections can be determined as shown in the Fig. 7.8.5.

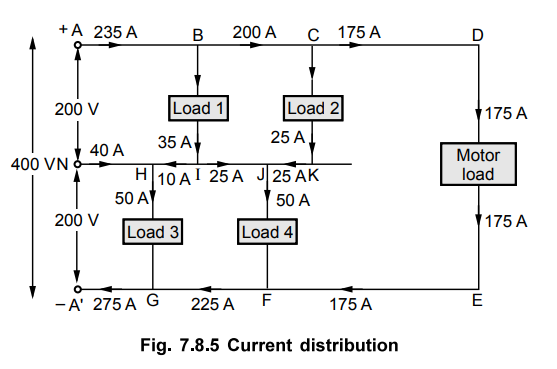
It can be seen that for the selected values, I₁ = 235 A while I₂ = 275 A.

Thus I₂ – I₁ = 275 - 235 A = 40 A current flows at the neutral point and its direction is from neutral end towards load end. Thus knowing currents in all the sections and resistances of all the sections, the voltage across any load can be determined by applying Kirchhoff's voltage law to the appropriate loop. Such a voltage is called load point voltage. While applying Kirchhoff's voltage law, care must be taken to consider the sign of the voltage drop correctly. If the potential across two points is traced from positive to negative as a drop then it must be taken as negative while if the potential is traced from negative to positive i.e. as a rise it must be taken as positive.

Example 7.8.1  A 3 wire d.c. system takes a current of 50 A on positive side and 45 A on negative side. The resistance of each outer is 0.0004 Ω per metre while the cross-section of middle wire is half of that of each outer. If the voltage between each outer and middle wire is maintained at 220 V at the feeding end, calculate the voltage at the distant load end between each outer and middle wire. The 3 wires are of 100 m length.

Solution : The system is shown in the Fig. 7.8.6.

Now I₁ = 50 A and I₂ = 45 A hence current through neutral wire is I₁ – I₂ = 5 A from load side to supply side.

Applying KVL to the loop ABCNA and taking potential drop as - ve and rise as + ve we can write,

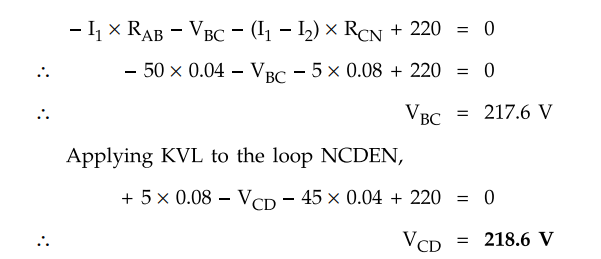
Applying KVL to the loop NCDEN,

+ 5 × 0.08 - V_CD - 45 × 0.04 + 220 = 0

V_CD = 218.6 V

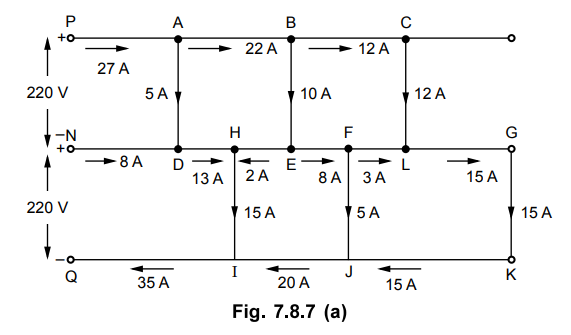
Example 7.8.2 A 3 wire d.c. distributor is fed at one end at 220 V between wires and middle wire as shown in Fig. 7.8.7. The numbers between section indicate the resistance of the respective section. Calculate the voltage between middle wire and outer at each load point.

AU : Dec.-11, Marks 16

Solution : By applying KCL, the currents in various sections can be obtained. The total current distribution is shown in the Fig. 7.8.7 (a). 

The voltage drops in the various sections are,

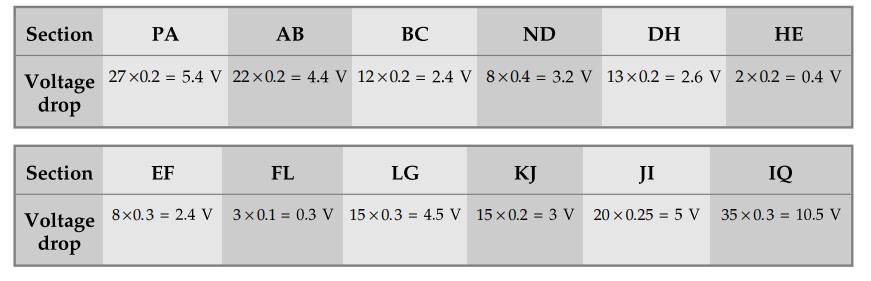
Applying KVL to the various loops,

Review Questions

1. Explain different methods to obtain 3-wire DC system.

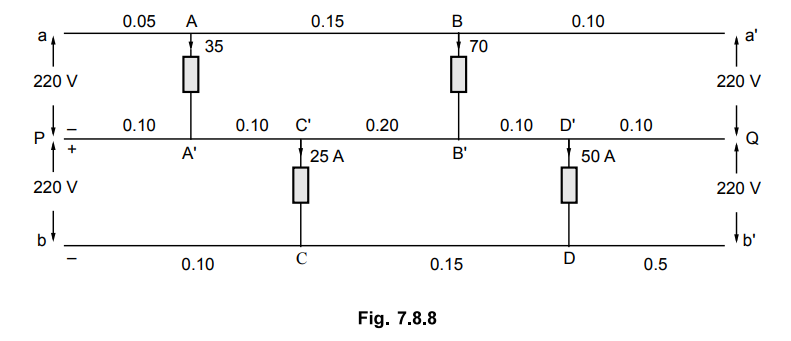
2. In the 3 wire d.c. distributor shown in the Fig. 7.8.8 the resistances of various sections shown are in ohms. Calculate the voltages at various load points.

[Ans.: 215.98 volts, 206.52 volts, 219.74 volts, 217.62 volts] 

3. A load supplied on a 3 wire d.c. system takes a current of 50 A on the positive side and 40 A on the negative side. The resistance of each outer wire is 0.1 Ω and the cross-section of the middle wire is one half that of the outer. If the system is supplied at 500 / 250 V, find the voltage at the load end between each outer and middle wire.     

[Ans.: 243 V, 248 V]