Design of Clock Sequential Circuits: State Reduction

Design of Clock Sequential Circuits

AU : May-07, 08, 10, 15, 16, June-09, Dec.-03, 05, 06, 07, 12

• The recommended steps for the design of a clocked synchronous sequential circuit are as follows :

1. It is necessary to first obtain the state table from the given circuit information such as a state diagram, a timing-diagram, or other pertinent information.

2. The number of states may be reduced by state reduction technique if the sequential circuit can be categorized by input-output relationships independent of the number of states.

3. Assign binary values to each state in the state table.

4. Determine the number of flip-flops needed and assign a letter symbol to each.

5. Choose the type of flip-flop to be used.

6. From the state table, derive the circuit excitation and output tables.

7. Using the K-map or any other simplification method, derive the circuit output functions and the flip-flop input functions.

8. Draw the logic diagram.

• Let us see the details of various steps involved in the design of clocked sequential circuits.

 

1. State Reduction

a. Row Elimination Technique

• The state reduction technique basically avoids the introduction of redundant states. The reduction in redundant states reduce the number of required flip-flops and logic gates, reducing the cost of the final circuit. The two states are said to be redundant or equivalent, if every possible set of inputs generate exactly same output and same next state. When two states are equivalent, one of them can be removed without altering the input-output relationship.

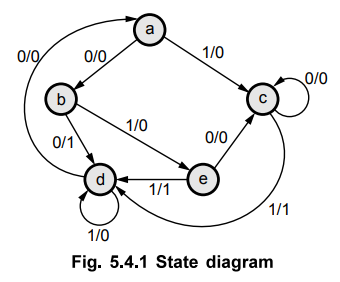
 • Let us illustrate the state reduction technique with an example. We start with a sequential circuit whose specification is given in the state diagram of Fig. 5.4.1. As shown in the diagram, the states are denoted by letter symbols instead of their binary values, because in state reduction technique internal states are not important; but only input-output sequences are important.

Step 1 : Determine the state table for given state diagram

Table 5.4.1 shows the state table for given state diagram

Step 2 : Find equivalent states

As mentioned earlier, in equivalent states every possible set of inputs generate exactly same output and same next state. In the given circuit there are two input combinations : X = 0 and X = 1. Looking at the state table for two present states that go to the same next state and have the same output for both input combinations, we can easily find that states c and e are equivalent. 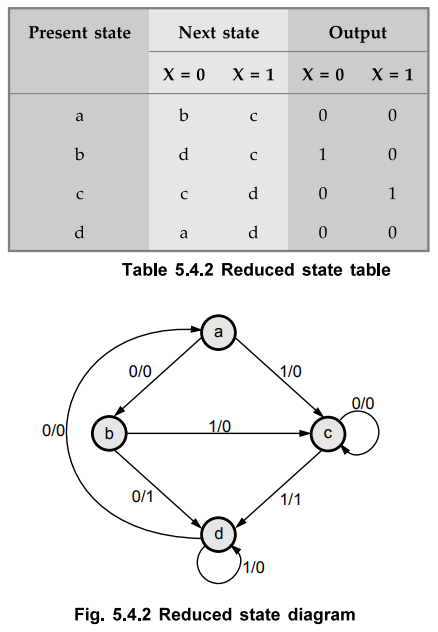This is because, c and e both states go to states c and d and have outputs of 0 and 1 for X = 0 and X = 1, respectively. Therefore, state e can be removed and replaced by c. The final reduced table is shown in Table 5.4.2. The state diagram for the reduced table consists of only four states and is shown in Fig. 5.4.2.

 

Examples for Understanding

Ex. 5.4.1 Minimize the state table shown given below.

AU : Dec.-03, Marks 4

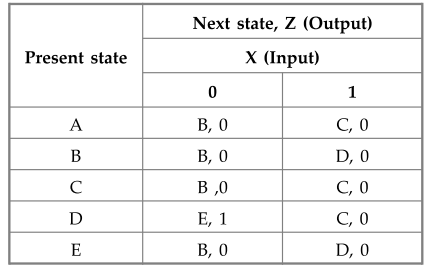
Sol. :

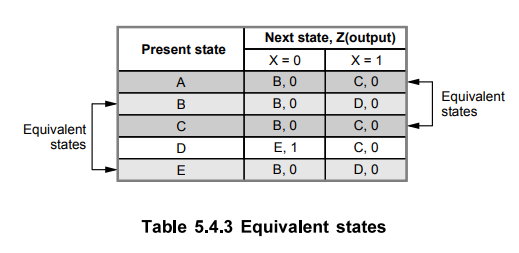
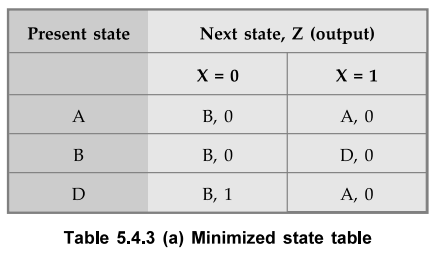
Step 1 : Find equivalent states. The Table 5.4.3 shows the equivalent states in the given state table. The states A and C, and states B and E generate exactly same output and same next state. Hence, state A and C are equivalent and similarly states B and E are equivalent.

Step 2 :

Replace redundant states with equivalent states.

Replace C by A and replace E by B, and remove states C and E.

Now, there are no equivalent states and hence Table 5.4.3 (a) shows the minimized state table.

 

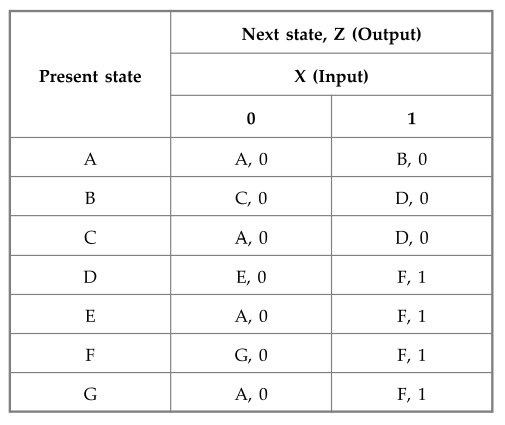
Ex. 5.4.2 Minimize the state table shown given below :

AU : Dec.-05, Marks 6

Sol . :

Step 1 : Find equivalent states

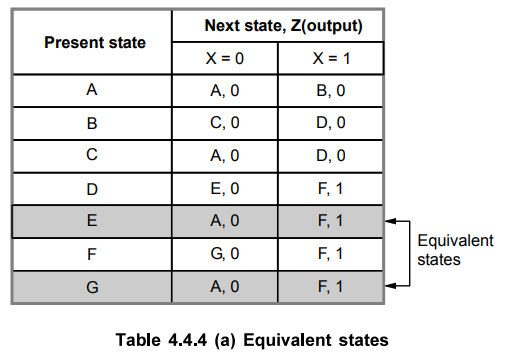
Step 2 : Replace redundant state with equivalent state.

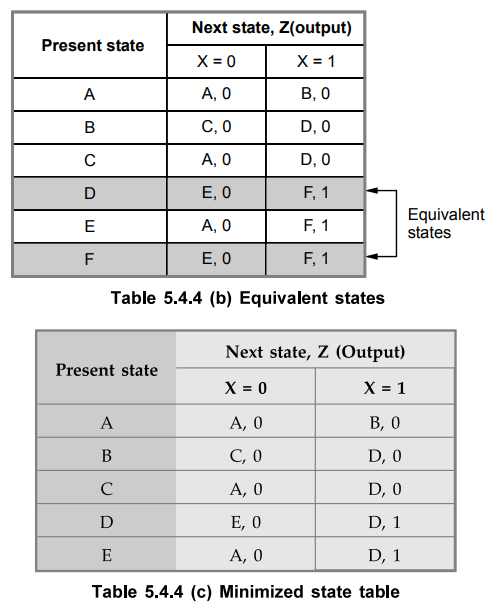
Therefore, replace G by E and remove state G. Looking at Table 5.4.4 (b), we find that states D and F are equivalent. Therefore, replace F by D and remove state F. Now, there are no equivalent states and hence Table 5.4.4 (c) shows the minimized state table.

 

Ex. 5.4.3 Construct reduced, state diagram for the following state diagram.

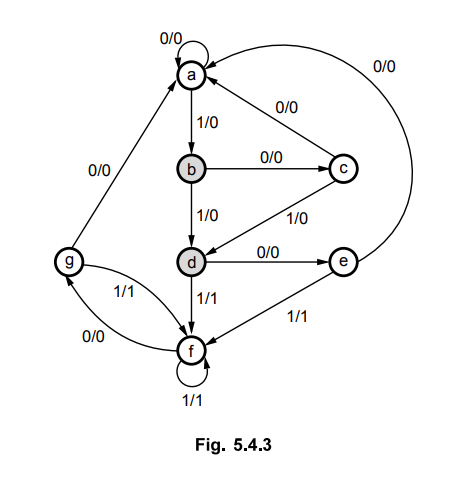
AU : May-13, Marks 16

Sol. : The state table for given state diagram is as shown in Table 5.4.5.

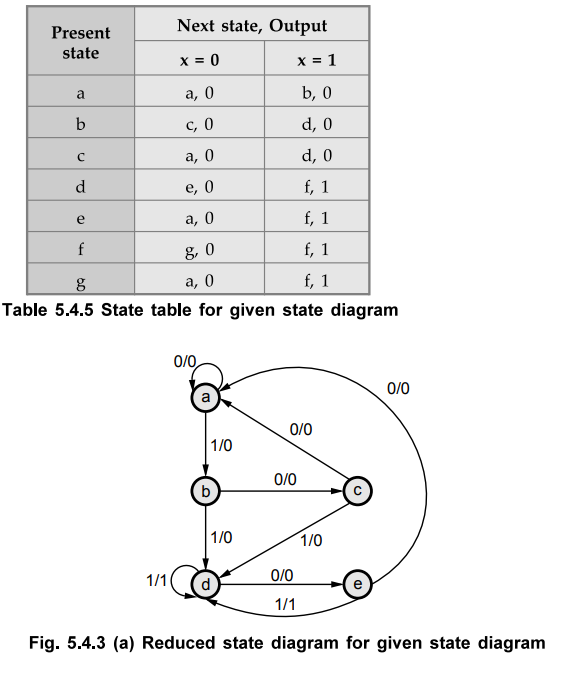
Referring example 5.4.2 we have reduced state table as shown in Table 5.4.4 (c). Fig. 5.4.3 (a) shows reduced state diagram drawn by referring state table of Table 5.4.4 (c).

 

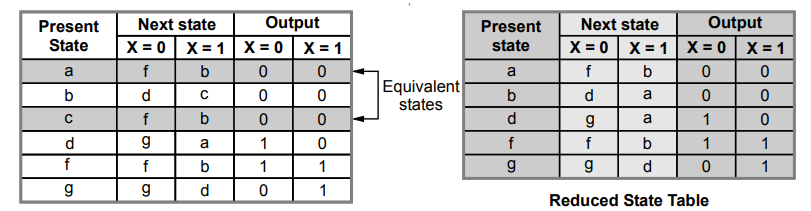
Ex. 5.4.4 i) Reduce the number of states in the following state table and tabulate the reduced state table.

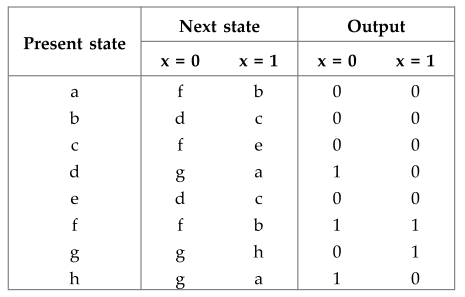
ii) Starting from state a, and input sequence 01110010011, determine the output sequence for the given and reduced state table.

Sol. :

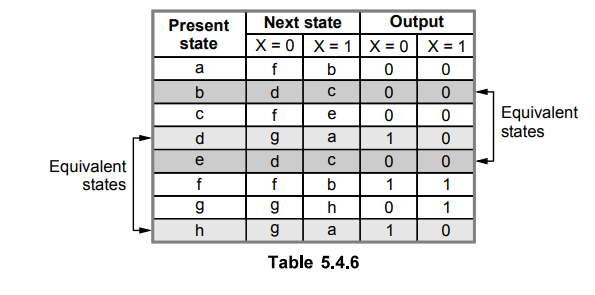
According to given state table we have states b and e, and states d and h are equivalent.

ii) Using reduced state table

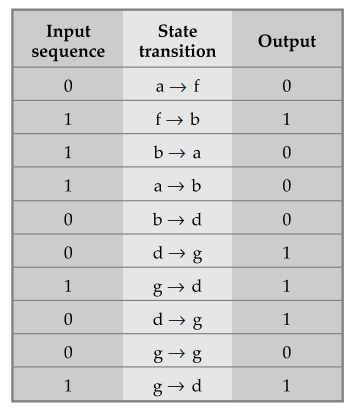
The output sequence for reduced state table is 01000111010

Using given state table

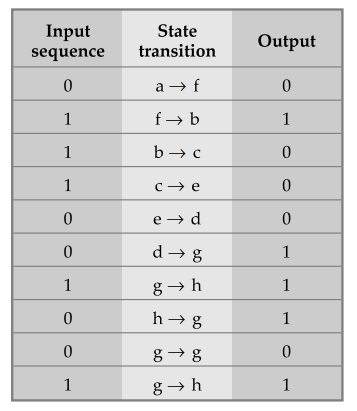
The output sequence for given state stable is also 01000111010.

b. Reduction of state Table Using Partition Technique

• A procedure for state minimization and determination of n-equivalence is discussed in the following example. Consider the state table given in Table 5.4.7 (a).

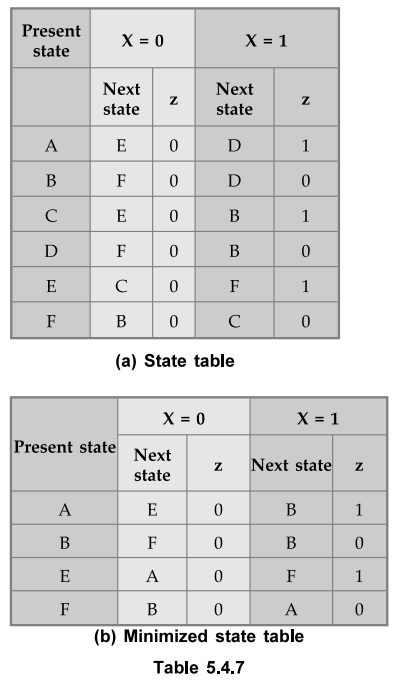
Step 1 : Partition the states into subsets such that all states in the same subsets are 1-equivalent.

• The first partition P^ can be obtained by placing those, states having the same outputs under all inputs, in the same block. This partitioning gives two subsets.

1. (A, C, E) : Their outputs are under 0 and 1 inputs are 0 and 1, respectively.

2. (B, D, F) : There outputs are under 0 and 1 inputs are 0 and 0, respectively.

P1 = (A, C, E) (B, D, F)

Step 2 : Partition the states into subsets such that all states in the same subsets are 2-equivalent.

• This can be accomplished by observing that two states are 2-equivalent if and only if they are 1-equivalent and their Ii-successors, for all possible Ii; are also 1-equivalent. In other words we can say that, two states are placed in the same block of partition P₂ if and only if they are in the same block of P₁ and for each possible Ii there Ii-successor are also contained in a block of Pi.

1. The 0 and 1-successors of (A, C, E) are (C, E) and (B, D, F), respectively, and since both are contained in common blocks of Plz the states (A, C, E) are 2-equivalent, and therefore (A, C, E) constitutes a block in P₂.

2. The 0-successor of (B, D, F) is (B, F) which contained in the common block of Pi; however 1-successor of (B, D, F) is (D, B, C) in which (D, B) and (C) are not contained in a single block of Pi. Therefore, the block (B, D, F) must be split into (BD) and (F)

P₂ = (A, C, E) (B, D) (F)

Step 3 : Partition the states into subsets such that all states in the same subsets are 3-equivalent.

• By applying same procedure in step 2, we can split block (A, C, E) of P2 into (A, C) and (E), since the 1-successor of (A, C, E) is (D, B, F) which is not in the single block of P₂.

P₃ = (A, C) (E) (B, D) (F)

• Further partitioning of states is not possible because we find that the 0 and 1-successors of blocks in P₃ are in the common block of P₃.

• The states in the common blocks of P3 are equivalent and redundant Therefore, state A = C and B = D. The states C and D are redundant states and can be eliminated to give minimised state table as shown in Table 5.4.7 (b).

• In general, we can say that, the PK +1 partition is obtained from PK by placing in the same block of PK + 1 those states which are in the same block of PK and whose I i-successors for every possible Ii are also in a common block of P_K .

• When P_{K + 1} = P_K, the partitioning process terminates and P_K defines the sets of equivalent states of the sequential machine. The P_K is thus called the equivalence partition and the partitioning procedure discussed above is referred to as the Moore reduction procedure.

 

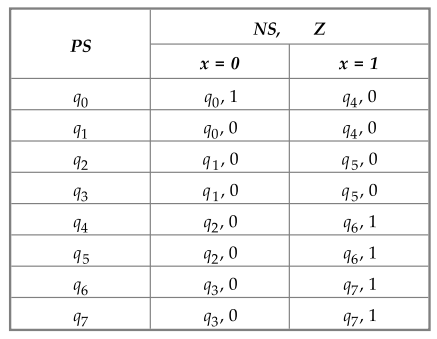
Ex. 5.4.5 Determine the minimal state equivalent of the state table given :

Sol. :

1. States having the same outputs, under all input conditions can be grouped as

P₁ : (q₀) (q₁, q₂, q₃) (q₄ , q₅ , q₆, q₇)

2. 1-successors of (q₁, q₂, q₃) are in two different blocks and therefore,

P₂ : (q₀) (q₁) ( q₂, q₃) (q₄ , q₅ , q₆, q₇)

3. l-successor of ( q₂, q₃) Mid (q₄ , q₅ , q₆, q₇) are in the common blocks of P₂.

Therefore,

P₃ : (q₀) (q₁) ( q₂, q₃) (q₄ , q₅ , q₆, q₇)

Thus equivalent states are :

q₂ = q₃ and q₄ = q₅ = q₆ = q₇

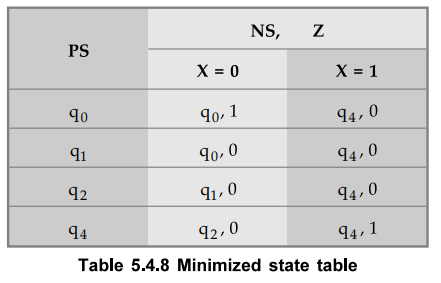
The resultant minimized state table is as shown in Table 5.4.8.

 

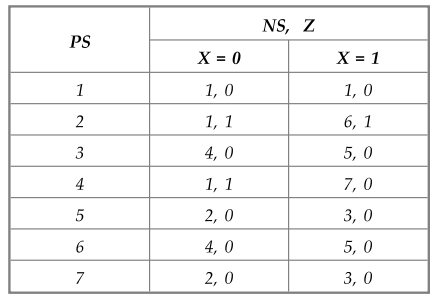
Ex. 5.4.6 Determine a minimal state table equivalent to the state table given :

Sol. :

1. States having the same outputs, under all input conditions can be grouped as

P₁ : (1, 3, 5, 6, 7) (2) (4)

2. 1-successors of (1, 3, 5, 6, 7) are (1, 4, 2, 4, 2) when X = 0 and (1, 5, 3, 5, 3) when X = 1, which are in different blocks and therefore,

P₂ : (1) (3, 6) (5, 7) (2) (4)

3. 1-successors of (3, 6) and (5, 7) are in the common block of P2. Therefore,

P₃ : (1) (3, 6) (5, 7) (2) (4)

Thus equivalent states are : 3 = 6 and 5 = 7

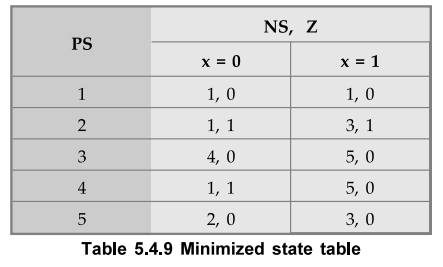
The resultant minimized state table is as shown in Table. 5.4.9.

 

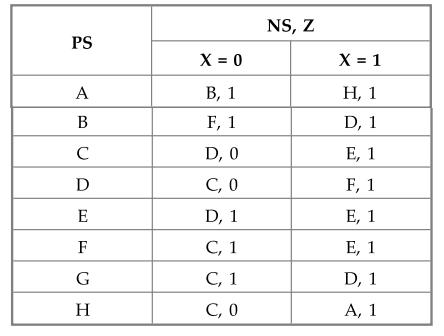
Ex. 5.4.7 Find the equivalence partition for the machine shown below.

i) Show a standard form of the corresponding reduced machine.

ii) Find a minimum length sequence that distinguishes state A from state B.

Sol. :

1. States having the same output, under all input conditions can be grouped as

P₁ : (A, B, E, F, G) (C, D, H)

2. 1-successor of (A, B, E, F, G) are (B, F, D, C, C) when X = 0 and (H, D, E, E, D)

When X = 1, which are in different blocks, therefore,

P₂ : (A, B) (E, F) (G) (C, D, H)

3. 1-successor of (A, B) are (B, F) when X = 0 which are in different blocks and 1-successor of (C, D, H) are (E, F, A) when X = 1 which are also in different blocks, therefore,

P₃ : (A) (B) (E, F) (G) (C, D) (H)

4. 1-successors of (E, F) and (C, D) are in the common block of P₃. Therefore,

P₄ : (A) (B) (E, F) (G) (C, D) (H)

Thus equivalent states are E = F and C = D

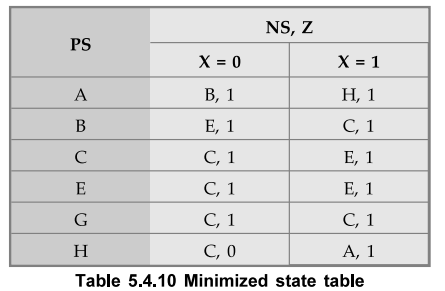
The resultant minimized state table is as shown in Table 5.4.10.

c. Reduction of State Table Using Merger Graph

Merger graphs is state reducing tool used to reduce states in the incompletely specified machine. The merger graph is defined as follows :

1. It contains the same number of vertices as the state table contains states.

2. Each compatible state pair is indicated by a line drawn between the two state vertices.

3. Every potentially compatible state pair, with outputs not in conflict but whose next states are different, is connected by a broken line. The implied states are drawn in the line break between the two potentially compatible states.

4. If two states are incompatible, no connecting line is drawn.

 

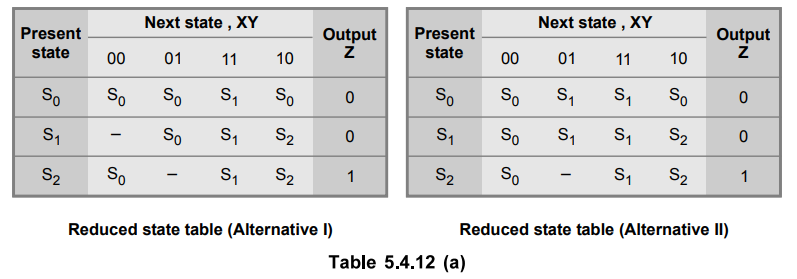
Ex. 5.4.8 Reduce the state table shown in Table 5.4.11 using Merger graph method.

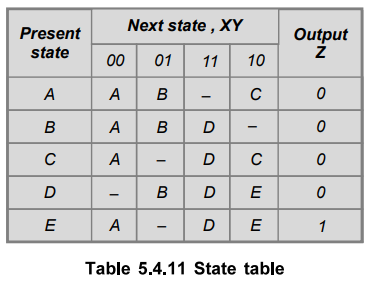
Sol . :

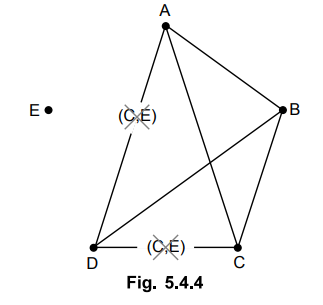
1. States A and B are compatible. Thus the line is drawn between A and B.

2. State A and C are compatible. Thus the line is drawn between A and C.

3. State B and C are compatible. Thus, the line is drawn between B and C.

4. States A and D are compatible only if implied states C and E are compatible. This is indicated by drawing a broken line between A and D with CE written in between.

5. States A and E are incompatible since there outputs are different, so line is not drawn between A and E. For the same reason states B, C and D are also not compatible with E.

6. State B and D are compatible. Thus, the line is drawn between B and D.

7. States C and D are compatible only if implied states C and E are compatible. This is indicated by drawing a broken line between C and D with CE written in between.

8. It is found that states C and E are not compatible and hence states A and D, and states D and C are also not compatible. This is indicated by cross (X) marks.

The compatibility lines of merger graph form a geometrical pattern consisting of one triangle (A, B, C), a line (B, D) and a single state E that is not compatible with any others. Thus maximum compatibles are :

(A, B, C) (B, D) (E)

Here, we can notice that state B is common in two sets. However, it can be compatible with either states A and C or state D, but not both. If we consider the next don't care state of B as state C, it is compatible with stable A and C. If we consider the next don't care state of B as state E it is compatible with state D.

Considering state B compatible with states A and C, we have following set of maximum compatibilities for given state table

(A, B, C) (D) (E)

Considering state B compatible with state D, we have following set of maximum compatibilities for given state table.

(A, C) (B, D) (E)

So we can say that there may be more than one possible way of merging rows when reducing a state table.

According to altemative-I we have

(A, B, C) → S₀

(D) → S₁

 (E) → S₂

and according to altemative-II we have

(A, C) → S₀

(B, D) → S₁

 (E) → S₂

The Table 5.4.12 (a) shows the reduced state table using both the alternatives.

 

Ex. 5.4.9 Reduce the given state table.

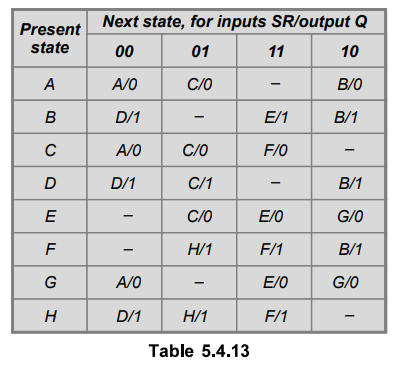
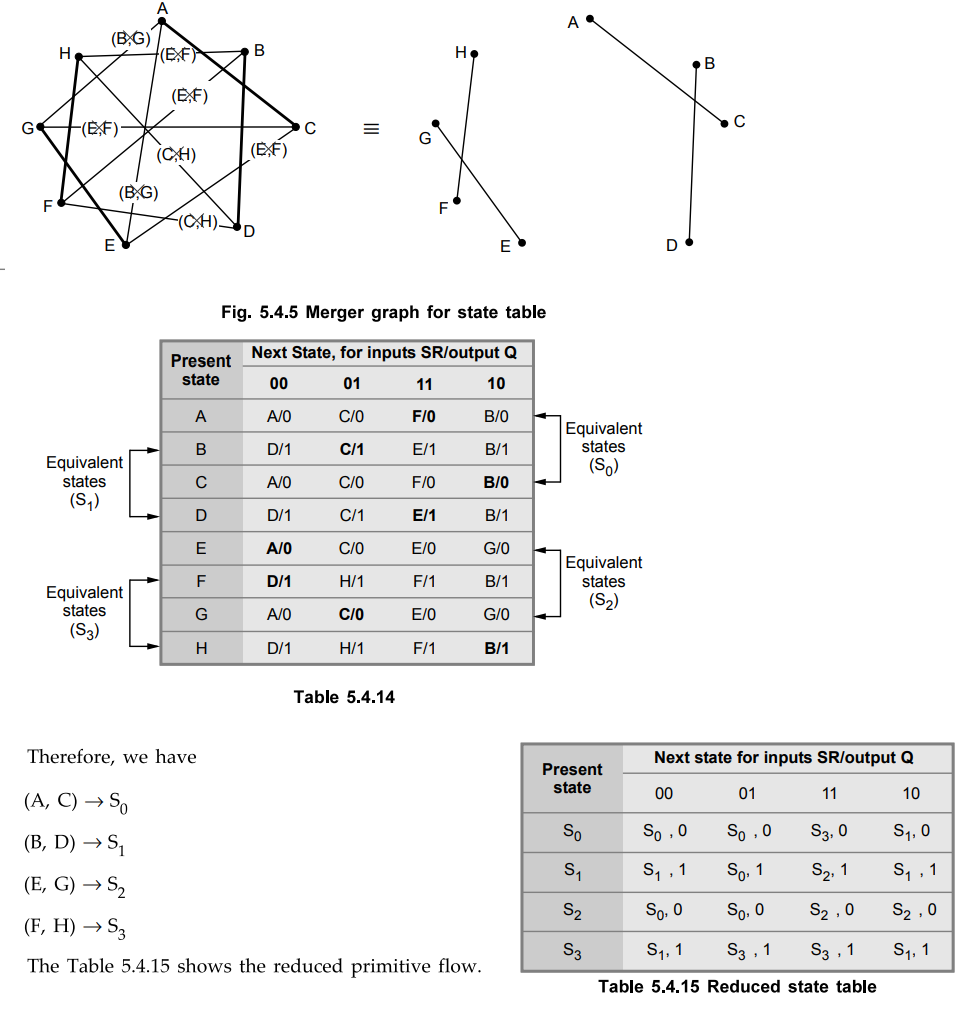
Sol. : The Fig. 5.4.5 shows the merger graph. Each compatible state pair is indicated by a line drawn between the two states vector.

Every potentially compatible state pair, with outputs not in conflict but whose next states are different, is connected by a broken line. The implied states are drawn in the line break between the two potentially compatible states. If two states are incompatible, no connecting line is drawn. 

d. Reduction of State Using Merger Table

• When performing state reduction of machines having a large number of states, it may be more convenient to find the compatible pair and their implications in a merger table, instead of using the merger graph. The merger table method is also called as Pauli-Unger method or implication chart method. The table shows the state table for sequential machine and its merger table in the Fig. 5.4.6.

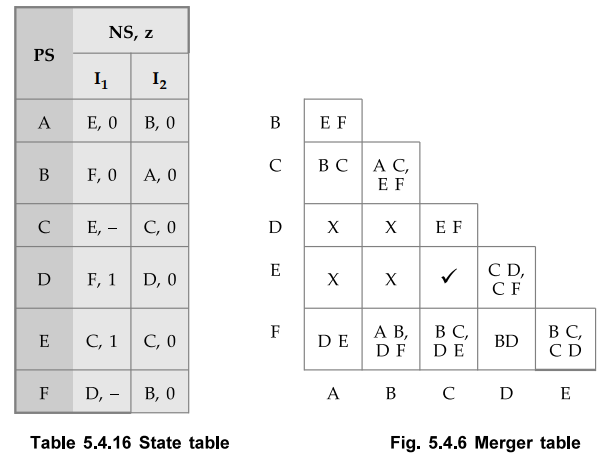
• Each cell of the merger table corresponds to the compatible pair represented by the intersection of the row and column headings. The incompatibility of two states is indicated by placing cross mark X in the corresponding cell, while their compatibility is indicated by placing check mark (✔) in the cell. For example, states A and D are incompatible because their outputs are conflicting and hence the cell corresponding them contain cross mark X. On the other hand, states C and E are compatible and hence the cell corresponding them contain cross mark X. On the other hand, states C and E are compatible and hence the cell corresponding them contain check mark ✔. The implied pair or pairs corresponding to state-pair are written with the cell, as shown in the Fig. 5.4.6. For example, states A and C are compatible only when implied states B and C are compatible, therefore implied pair B C is written in the cell corresponding to states A and C. In the similar way the entire merger table is written. Now it is necessary check whether implied pairs are compatible or not. This can be checked by observing the merger table. The implied states are incompatible if corresponding cell contain X. For example, implied pair BD is incompatible because cell BD contain X. Since BD is incompatible, states D and F are also incompatible. As DF is compatible, states B and F are also incompatible. It is indicated by cross mark in Fig. 5.4.6.

• Once the merger table is completed, the set of all maximal compatibles can be found by procedure which is counter part to that of finding complete polygon in the merger graph. The procedure is as follows :

1. Begin with right most column in the merger table and proceed left unit a column containing a compatible pair is encountered. For example, the pair EF in the merger table shown in Fig. 5.4.6.

2. Proceed left to the next column containing at least one compatible pair. If the state to which this column corresponds is compatible with all the states in the set of previously determined compatible states then add this state to that set of compatible states to form a larger compatible. If the state is not compatible with all the states of previously determined set, but is compatible with some other state, form a new set of compatible states. For example, state D is not compatible with both E and F which are previously determined set of states. However, it is compatible with state E. Therefore, it is not added in the previous set, but the new set is formed, DE. On the other hand, state C is compatible with both E and F which are previously determined set of states and hence it is included in that set to form a new set CEF. Similarly, C is also included in set DE to get a new set CDE.

3. Repeat step 2 until the left most column is reached.

After application of above mentioned procedure the merger table in Fig. 5.4.6, gives following set of maximal compatibles.

Column E : (E, F)

Column D   : (E, F); (D, E)

Column C   : (C, E, F);   (C, D, E)

Column B   : (C, E, F);   (C, D, E);    (B, C)

Column A   : (C, E, F);   (C, D, E);    (A, B, C); (A, C, F)

• The right most column is E. It indicates that the state E is compatible with state F, resulting a compatible pair (EF). The column D indicates that the state D is compatible with state E, thus compatible pair (DE) is included in the compatible list. The column C shows that the state C is compatible with states D, E and F and consequently the compatibles generated previously are enlarged to include state C. The column B consists of a single compatible pair (BC), which is added to the previously generated compatible list. The column A indicates that the state A is compatible with states B, C and F. Thus, the previously generated compatible pair (BC) is enlarged to give the compatible (ABC), while rows C and F, together with preciously available compatibility relations, give the compatible (ACF). Therefore, the set of maximal compatibles is

(C, E, F); (C, D, E); (A, B, C); (A, C, F)