Design of Synchronous Counters

Design of Synchronous Counters

AU: Dec.-03, 07, 09, 11, 12, 15, 16, May-03, 04, 05, 10, 11, 15

1. Determine the number of flip-flops needed. If n represents number of flip-flops 2ⁿ ≥ number of states in the counter.

2. Choose the type of flip-flops to be used.

3. Using excitation table for selected flip-flop determine the excitation table for the counter.

4. Use K-map or any other simplification method to derive the flip-flop input functions.

5. Draw the logic diagram.

 

Ex. 5.9.1 Design a MOD-5 synchronous counter using JK flip-flops and implement it. Also draw the timing diagram.

AU May-15, Marks 8

Sol. :

Step 1: Determine the number of flip-flop needed

Flip-flops required are

Here

2ⁿ ≥ N

N = 5

n = 3 i.e. three flip-flops are required.

Step 2 : Type of flip-flop to be used : JK

Step 3 : Determine the excitation table for the counter.

Step 4 : K-Map Simplification

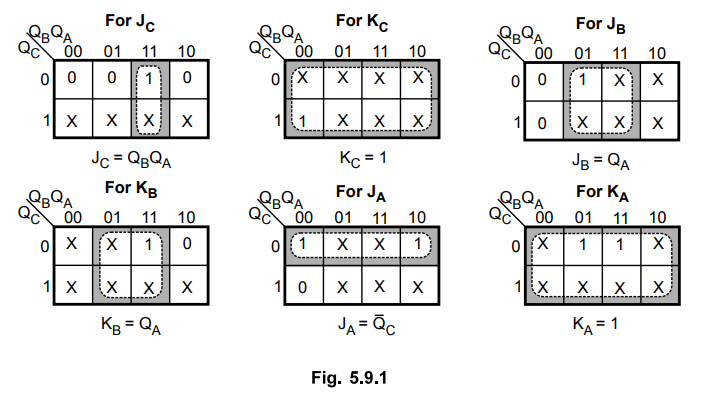
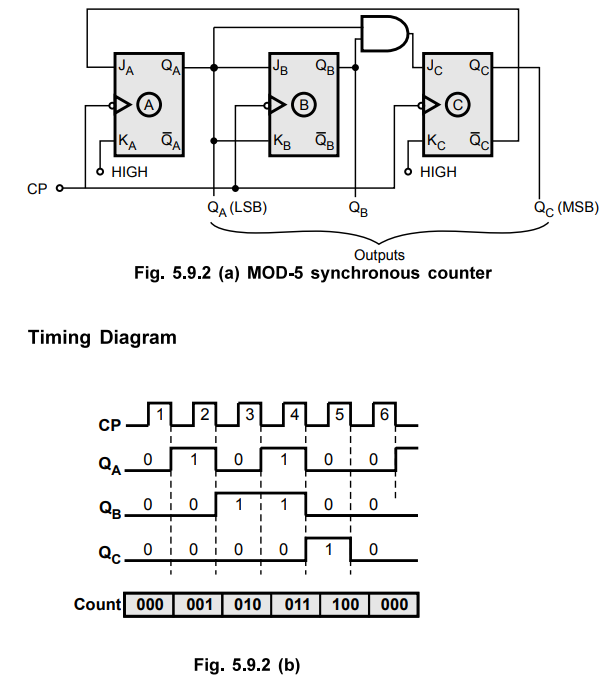
Step 5 : Draw the logic diagram

Ex. 5.9.2 Design divide by 6 counter using T-flip-flops. Write state table and reduce the expression using K-map.

Sol. :

Step 1 : Determine the number of flip-flops needed.

For designing mod 6 counter using the formula

2ⁿ ≥ N

Here  N = 6 n = 3 i.e. 3 flip-flops are required.

Step 2 : Type of flip-flops to be used : T

Step 3 : Determine the excitation table for counter.

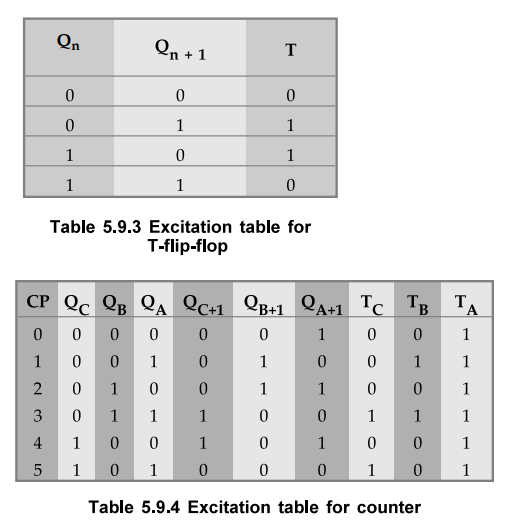
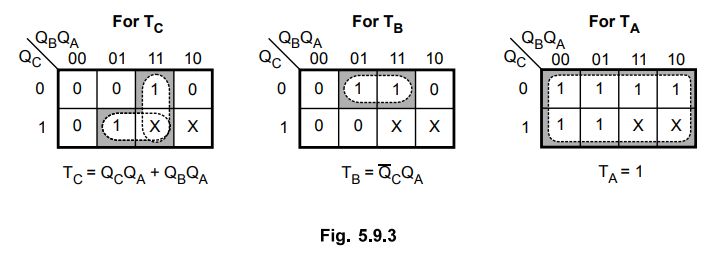
Step 4 : K-map simplification.

 Step 5 : Draw the logic diagram.

 

 

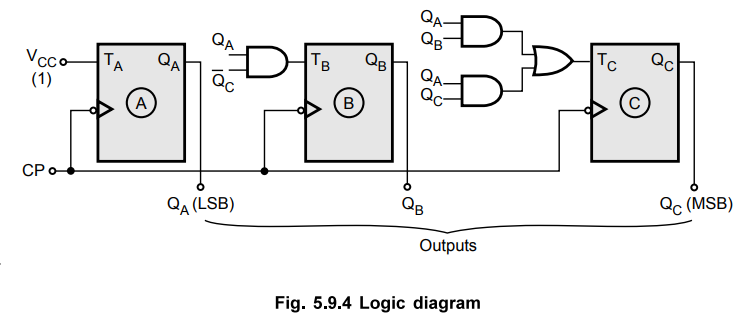
Ex. 5.9.3 Using positive edge triggering SR flip-flops design a counter which counts in the following sequence : 000, 111, 110, 101, 100, Oil, 010, 001, 000, ....

Sol. :

Step 1 : Determine the number of flip-flops needed

We know that 2ⁿ ≥ N. Here, N = 8  n = 3

Step 2 : Type of flip-flop to be used : SR

Step 3 : Determine the excitation table for counter.

Here, the next state for each present state is written according to given sequence. For example, the next state for the present state 000 is 111.

Step 4 : K-map simplification.

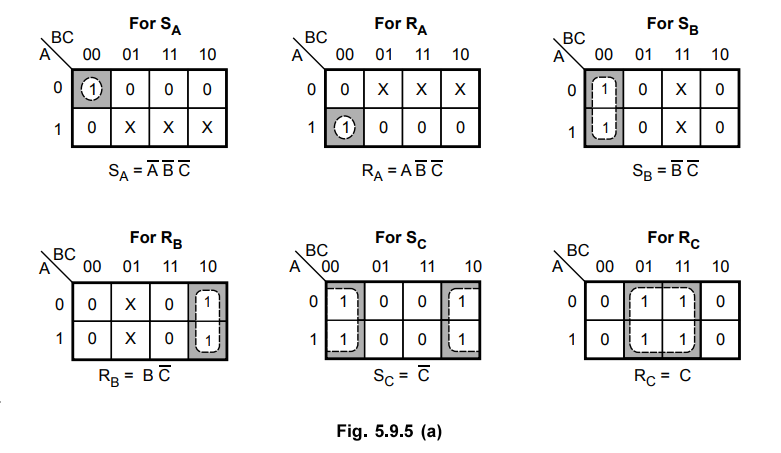
Step 5 : Draw logic diagram

Ex. 5.9.4 Design a synchronous decade counter using D flip-flop.

Sol. : The decade counter is a mod-10 counter. It has ten states : 0 - 9.

Step 1 : Determine the number of flip-flops needed.

We know that 2ⁿ ≥ N. Here, N = 10 n = 4 i.e. 4 flip-flops needed.

Step 2 : Type of flip-flops to be used : D

Step 3 : Determine the excitation table for counter.

Step 4 : K-map simplification

Step 5 : Draw the logic diagram.

 

Ex. 5.9.5 Design a counter with the sequence 0,1, 3, 7, 6,4, 0.

Sol. :

Step 1 : Determine the number of flip-flops needed. 7 = (111)₂ which is 3-bit. Thus, we need 3-flip-flops.

Step 2 : Flip-flops to be used : JK.

Step 3 : Determine the excitation table for counter. Here, the next state for each present state is written according to given sequence. For example, the next state for the present state 3 (Oil) is 7 (111). The counts which are not in sequence are treated as don't cares.

Step 4 : K-map simplification

Step 5 : Draw the logic diagram

 

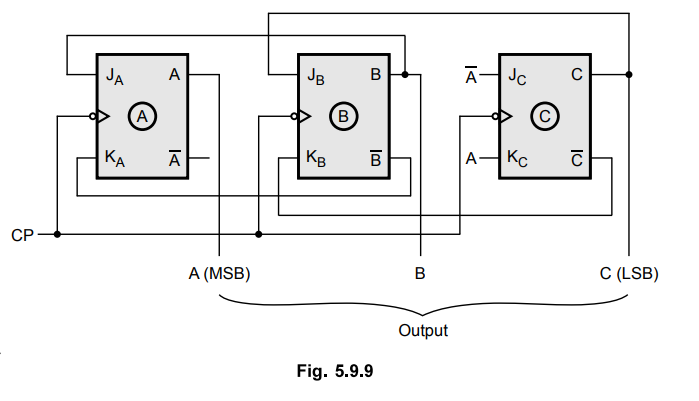
Ex. 5.9.6 Design a BCD up/down counter using SR flip-flops.

Sol. :

Step 1 : Number of flip-flops needed = 4

Step 2 : Flip-flops to be used = SR

Step 3 : Excitation table for counter

Step 4 : K-map simplification

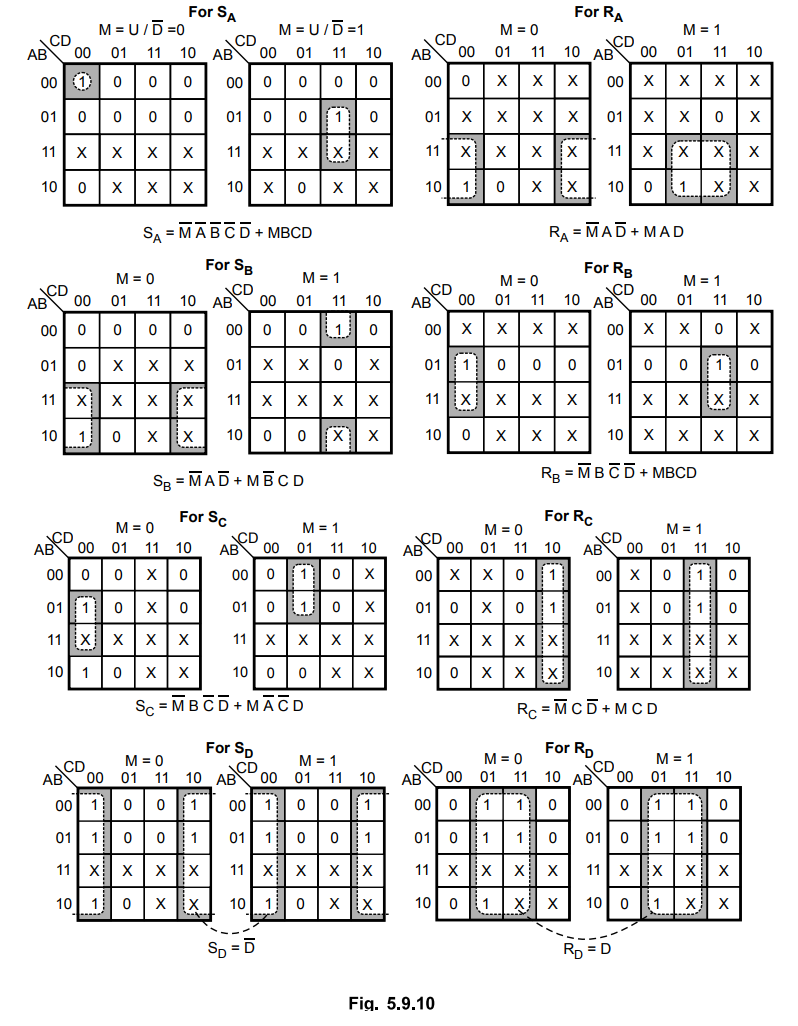
Step 5 : Logic diagram

 

Ex. 5.9.7 Design a synchronous counter using JK flip-flop to count the following sequence 7, 4, 3, 1, 6, 0, 7      

AU : May-09, Marks 16

Sol. :

Step 1 : Since 2³ > 7, three flip-flops are required

Step 2 : Flip-flops to be used : JK

Step 3 : Excitation table for counter

 

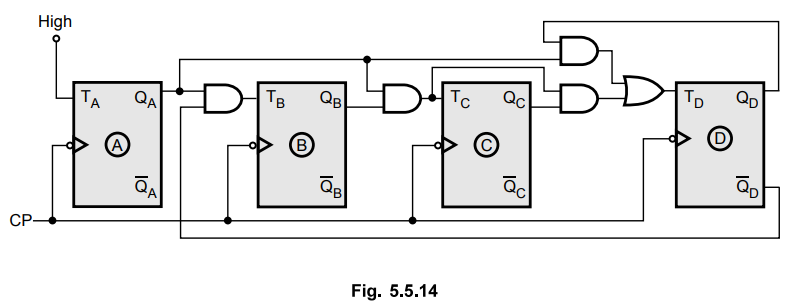
Ex. 5.9.8 Design and implement a synchronous decade counter using T flip-flop. Draw the timing diagram.

AU : May-08, 10, 11, Dec.-15, Marks 16

Sol. :

Step 1 : Since N = 10, n = 4 i.e. flip-flops needed = 4

Step 2 : Flip-flops to be used : T

Step 3 : Determine excitation table for counter

Step 4 : K-map simplification

Step 5 : Logic diagram

Step 6 : Timing diagram

Fig. 5.9.15 shows the timing diagram for the synchronous decade counter.

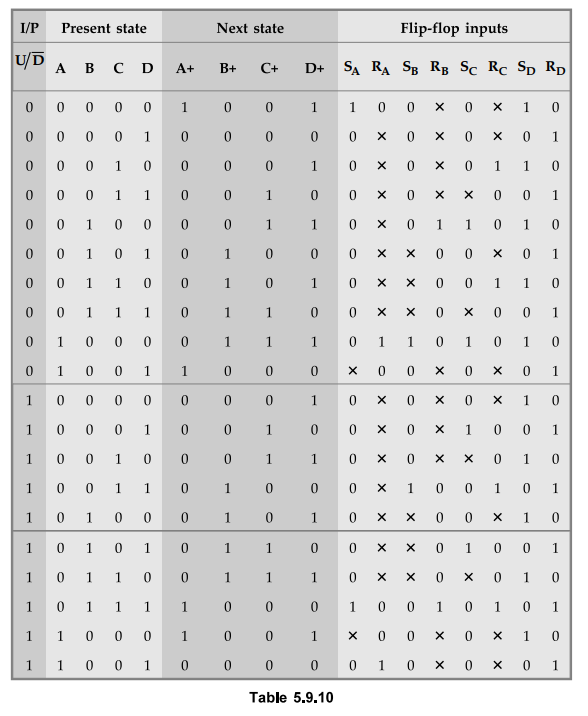
Ex. 5.9.9 Design a 3-bit synchronous updown counter using T flip-flops.

Sol. : Table 5.9.12 shows the excitation table for 3-bit up/down synchronous counter using T flip-flops.

Excitation table

K-map simplification

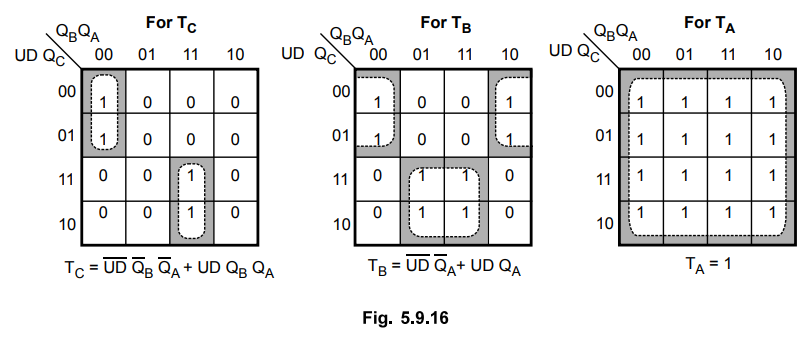
Logic diagram

 

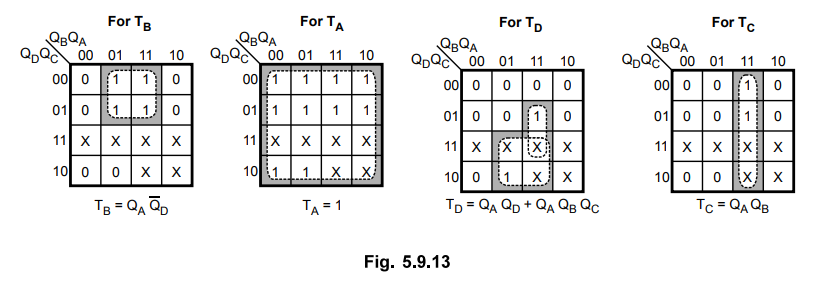
Ex. 5.9.10 Design a three bit binary counter using T flip-flops.

Sol. : Table 5.9.13 shows the excitation table for 3-bit binary counter.

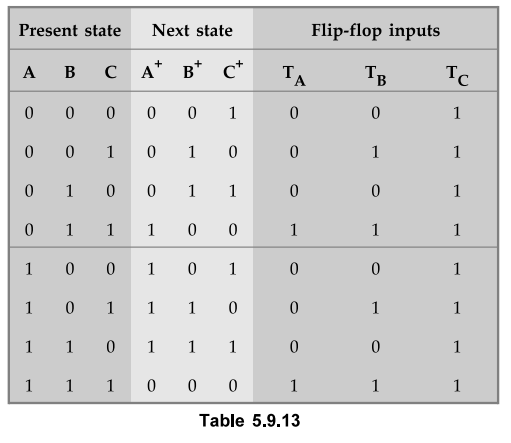
K-map simplification

Logic diagram

Ex. 5.9.11 Design and explain the working of a synchronous mod-3 counter.

AU : CSE : May-03, Marks 16

Sol. : N = 3 and

Step 1 : Since 2² > 3, n = 2 i.e. flip-flops needed = 2.

Step 2 : Flip-Flops used : JK

Step 3 : Transition table

Step 4 : K-map simplification

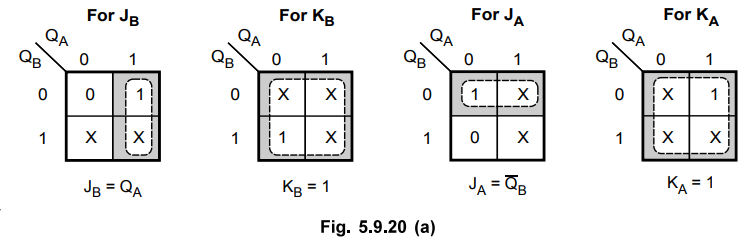
Step 5 : Logic diagram

Ex. 5.9.12 Design and explain the working of mod-7 counter.

Sol. :

Step 1 : N = 7, and since 2³ > 7, n = 3 i.e. Flip-Flops needed = 3

Step 2 : Flip-Flops used : JK

Step 3 : Transition table

Step 4 : K-map simplification

Step 5 : Logic diagram

 

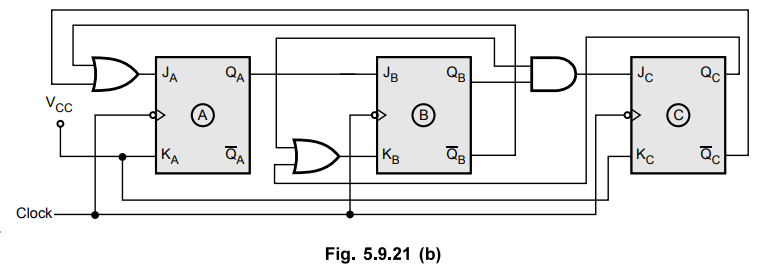
Ex. 5.9.13 Design a synchronous counter with states 0, 1, 2, 3, 0, 1. …… using JK FFs. AU : CSE : May-04, Marks 16

Sol. :

Step 1 : Here, N = 4 and since 2² ≥  4 we need 2 Flip-Flops

Step 2 : Flip-Flops to be used : JK

Step 3 : Transition table

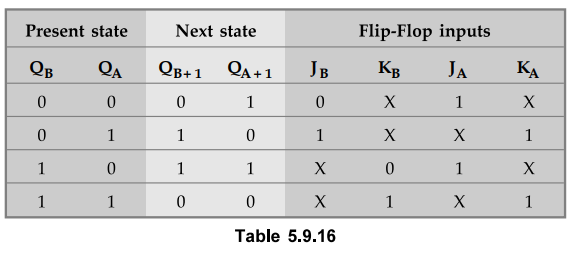
Step 4 : K-map simplification

Step 5 : Logic diagram

 

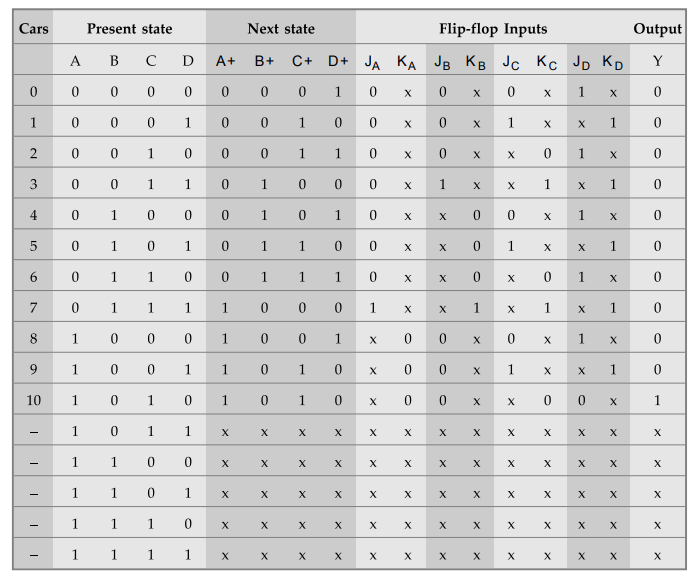
Ex. 5.9.14 Assume that there is a parking area in a shop whose capacity is 10. No more than 10 cars are allowed inside the parking area and the gate is closed as soon as the capacity is reached. There is a gate sensor to detect the entry of car which is to be synchronized with the block pulse. Design and implement a suitable counter using JK flip flops. Also, determine the number of flip flops to be used if the capacity is increased to 50.

Sol. : State Table

K-map Simplification

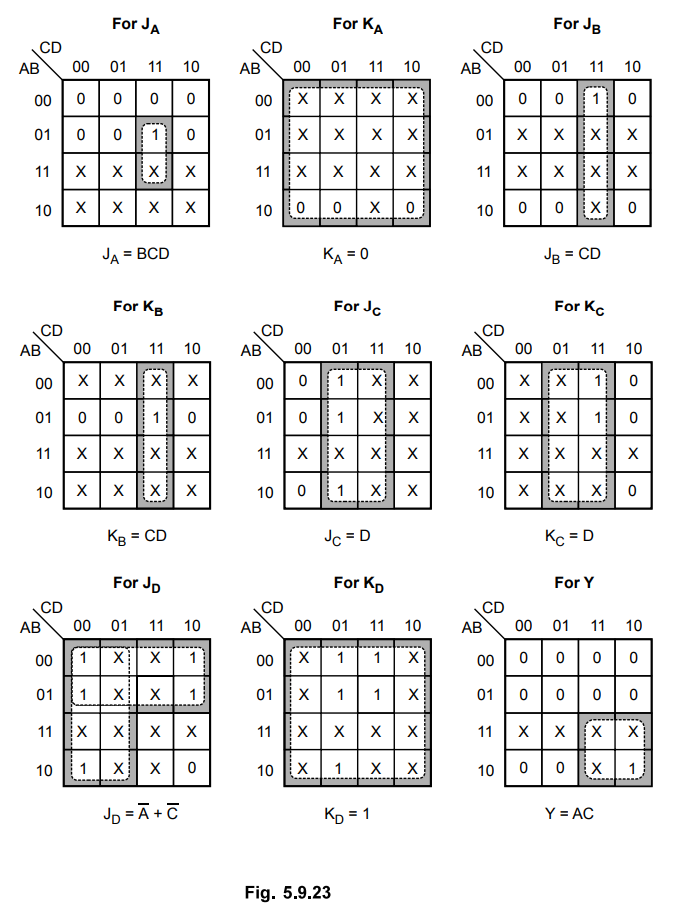
Logic Diagram