Determination of Xd and Xq using Slip Test

Determination of X_d and X_q using Slip Test

The method used to determine X_d and X_q, the direct and quadrature axis reactances is called slip test.

In an alternator we apply excitation to the field winding and voltage gets induced in the armature. But in the slip test, a three phase supply is applied to the armature, having voltage much less than the rated voltage while n the field winding circuit is kept open. The circuit diagram is shown in the Fig. 3.11.1.

The alternator is run at a speed close to synchronous but little less than synchronous value.

The three phase currents drawn by the armature from a three phase supply produce a rotating flux. Thus the armature m.m.f. wave is rotating at synchronous speed as shown in the Fig. 3.11.2.

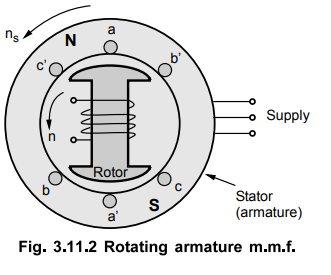
Note that the armature is stationary, but the flux and hence m.m.f. wave produced by three phase armature currents is rotating. This is similar to the rotating magnetic field existing in an induction motor.

The rotor is made to rotate at a speed little less than the synchronous speed. Thus armature m.m.f. having synchronous speed, moves slowly past the field poles at a slip speed (n_g - n) where n is actual speed of rotor. This causes an e.m.f. to be induced in the field circuit.

When the stator m.m.f. is aligned with the d-axis of field poles then flux (d per pole is set up and the effective reactance offered by the alternator is X_d.

When the stator m.m.f. is aligned with the q-axis of field poles then flux ( per pole is set up and the effective reactance offered by the alternator is X_q.

As the air gap is nonuniform, the reactance offered also varies and hence current drawn by the armature also varies cyclically at twice the slip frequency.

The r.m.s. current is minimum when machine reactance is X_d and it is maximum when machine reactance is X_q. As the reactance offered varies due to nonuniform air gap, the voltage drops also varies cyclically. Hence the impedance of the alternator also varies cyclically. The terminal voltage also varies cyclically. The voltage at terminals is maximum when current and various drops are minimum while voltage at terminals is minimum when current and various drops are maximum.

The waveforms of voltage induced in rotor, terminal voltage and current drawn by armature are shown in the Fig. 3.11.3.

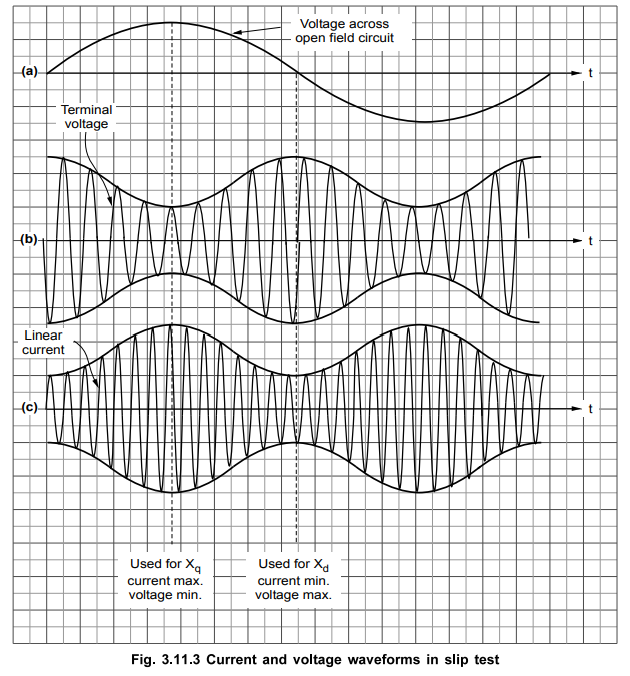
 It can be observed that when rotor field is aligned with the armature its flux

linkages are maximum, but the rate of change of flux is zero. Hence voltage induced in field goes through zero at this instant. This is the position where alternator offers reactance X_d. While when rate of change of flux associated with rotor is maximum, voltage induced in field goes through its maximum. This is the position where alternator offers reactance X_q.

The reactances can be calculated as,

Example 3.11.1 An alternator has a direct axis synchronous reactance of 0.7 per unit and a quadrature axis synchronous reactance of 0.4 per unit. It is used to supply full load at rated voltage at 0.8 pf. Find the total induced e.m.f. on open circuit.

Solution : The given values are,

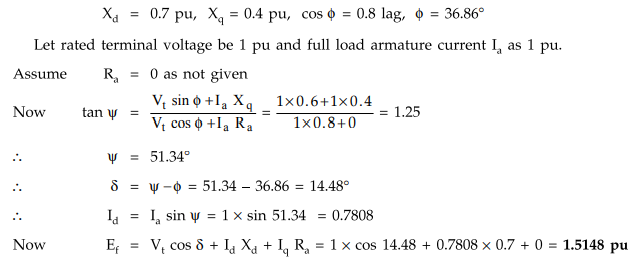
Example 3.11.2. A 400 V, 50 Hz delta connected alternator has a direct axis reactance of 0.1 Q and a quadrature axis reactance of 0.07 Q per phase. The armature resistance is negligible. The alternator is supplying 1000 A at 0.8 pf. lagging pf. i) Find the excitation emf neglecting saliency and assuming X_s = X_d; ii) Find the excitation e.m.f. taking into account the saliency.

Solution :

Example 3.11.3. A salient pole alternator has direct axis and quadrature axis reactances of 0.8 p.u. and 0.5 p.u. respectively. The effective resistance is 0.02 p.u. Compute percentage regulation when the generator is delivering rated load at 0.8 pf. lag and lead. Assume rated voltage and rated current as one per unit.

Example 3.11.4. A 50 Hz, 3-phase, 480 V, delta connected salient pole synchronous generator has X_d = 0.1 ohm and X_q = 0.075 ohm. The generator is supplying 1200 A at 0.8 p.f. lagging. Find the excitation e.m.f. Neglect armature resistance.

Solution :

Alternate solution :

The problem can also be solved on equivalent star basis. So converting values of X_d and X_q from delta into star.

Example 3.11.5. A 3-phase star-connected salient pole synchronous generator is driven at a speed near synchronous with the field circuit open and the stator is supplied from a balanced 3-phase supply. Voltmeter connected across the line gave minimum and maximum readings of 2800 volts and 2820 volts. The line current fluctuated between 360 A and 275 A. Find the direct and quadrature-axis reactances per phase. Neglect armature resistance.

Solution :

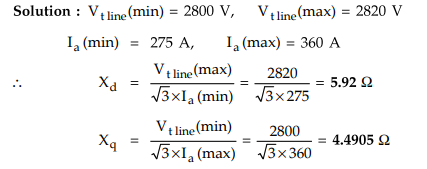
Examples for Practice

Example 3.11.6 A 230 V, 3 phase, 5 kVA star connected salient pole alternator with Xd = 12 Ω and = 7 V delivers full load current at unity power factor. Calculate the excitation voltage neglecting resistance.

[Ans.: E_f = 193.842 V]

Example 3.11.7 A synchronous generator has a direct axis synchronous reactance of 0.8 per unit and a quadrature axis synchronous reactance of 0.5 per unit. It is supplying full load at rated voltage at 0.8 p.f. lagging. Find the open circuit voltage.

[Ans.: E_f = 1.602 pu]

Example 3.11.8 A 3 phase star connected synchronous generator supplies current of 10 A having phase angle of 20° lagging at 400 V. Find the load angle and components of armature current I_a and I_q if X_d = 10 Ω and X_q = 6,5 Ω. Assume armature resistance to be negligible.

[Ans.: 8.23^o, I_d = 4.7301 A, I_q = 8.8105 A]

Example 3.11.9 Two identical round rotor alternators supply inductive load of 1.414 p.u. at 0.707 p.f. lagging and at rated voltage p.u. synchronous reactance of each is 0.6. Find e.m.f. and power angle. State assumptions made.

[Ans.: 0.8573 p.u., 16.58 °]

Review Question

1. Explain the determination of direct and quadrature axis synchronous reactance using the slip test. AU : May-06, 11, 13, 14, Dec.-ll, 17 Marks 8