Dielectric Materials

Dielectric Materials

AU ; May-04,18, Dec.-06, 12, 14, 17,18, Nov.-03, 11, Dec.-17

• It is seen that the conductors have large number of free electrons while insulators and dielectric materials do not have free charges. The charges in dielectrics are bound by the finite forces and hence called bound charges. As they are bound and not free, they cannot contribute to the conduction process. But if subjected to an electric field   , they shift their relative positions, against the normal molecular and atomic forces. This shift in the relative positions of bound charges, allows the dielectric to store the energy.

• The shifts in positive and negative charges are in opposite directions and under the influence of an applied electric field    such charges act like small electric dipoles.

Key Point : When the dipole results from the displacement of the bound charges, the dielectric is said to be polarized.

• And these electric dipoles produce an electric field which opposes the externally applied electric field. This process, due to which separation of bound charges results to produce electric dipoles, under the influence of electric field   , is called polarization.

 

1. Polarization

• To understand the polarization, consider an atom of a dielectric. This consists of a nucleus with positive charge and negative charges in the form of revolving electrons in the orbits. The negative charge is thus considered to be in the form of cloud of electrons. This is shown in the Fig. 5.6.1.

• Note that    applied is zero. The number of positive charges is same as negative charges and hence atom is electrically neutral. Due to symmetry, both positive and negative charges can be assumed to be point charges of equal amount, coinciding at the centre. Hence there cannot exist an electric dipole. This is called unpolarized atom.

• When electric field    is applied, the symmetrical distribution of charges gets disturbed. The positive charges experience a force  while the negative charges experience a force  in the opposite direction.

• Now there is separation between the nucleus and the centre of the electron cloud as shown in the Fig. 5.6.2 (a). Such an atom is called polarized atom.

• It can be seen that an electron cloud has a centre separated from the nucleus. This forms an electric dipole. The equivalent dipole formed is shown in the Fig. 5.6.2 (b). The dipole gets aligned with the applied field. This process is called polarization of dielectrics. 

There are two types of dielectrics,

1. Nonpolar and 2. Polar.

• In nonpolar molecules, the dipole arrangement is totally absent, in absence of electric field  It results only when an externally field  is applied to it. In polar molecules, the permanent displacements between centres of positive and negative charges exist. Thus dipole arrangements exist without application of . But such dipoles are randomly oriented. Under the application of , the dipoles experience torque and they align with the direction of the applied field . This is called polarization of polar molecules.

• The examples of nonpolar molecules are hydrogen, oxygen and the rare gases. The examples of polar molecules are water, sulphur dioxide, hydrochloric acid etc.

 

2. Mathematical Expression for Polarization

• When the dipole is formed due to polarization, there exists an electric dipole moment  

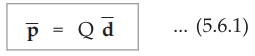
where  Q = Magnitude of one of the two charges

 = Distance vector from negative to positive charge

Let     n = Number of dipoles per unit volume

Δv = Total volume of the dielectric

N = Total dipoles = n Δv

• Then the total dipole moment is to be obtained using superposition principle as,

• If dipoles are randomly oriented,  is zero but if dipoles are aligned in the direction of applied  then  has a significant value.

• The polarization   is defined as the total dipole moment per unit volume.

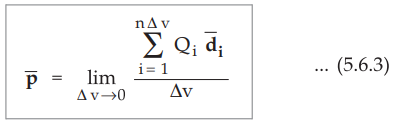
• It is measured in coulombs per square metre (C/m² ).

• It can be seen that the units of polarization are same as that of flux density . Thus polarization increases the electric flux density in a dielectric medium. Hence we can write, flux density in a dielectric is,

• For isotropic and linear medium, the 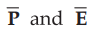 are parallel to each other at every point and related to each other as below

where xe = Dimensionless quantity called electric susceptibility of the material.

• The susceptibility tells us how sensitive is a given dielectric to the applied electric field  .

• Substituting (5.6.5) in (5.6.4),

• The quantity x e +1 is defined as   relative

permittivity or dielectric constant of the dielectric material. 

ƐR = Xe + 1 ... (5.6.9)

• The medium is said to be isotropic if 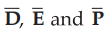 are parallel i.e. in the same direction. Thus their properties are same in all directions for isotropic medium.

• Note that in anisotropic or nonisotropic materials the 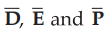 are not parallel to each other and Ɛ and % e vary in all directions and have nine different components. The discussion of anisotropic materials is beyond the scope of this book. 

 

3. Properties of Dielectric Materials

• The various properties of dielectric materials are,

1. The dielectrics do not contain any free charges but contain bound charges.

2. Bound charges are under the internal molecular and atomic forces and cannot contribute to the conduction.

3. When subjected to an external field  , the bound charges shift their relative positions. Due to this, small electric dipoles get induced inside the dielectric. This is called polarization.

4. Due to the polarization, the dielectrics can store the energy.

5. Due to the polarization, the flux density of the dielectric increases by amount equal to the polarization.

6. The induced dipoles produce their own electric field and align in the direction of the applied electric field.

7. When polarization occurs, the volume charge density is formed inside the dielectric while the surface charge density is form ed over the surface of the dielectric.

8. The electric field outside and inside the dielectric gets modified due to the induced electric dipoles.

 

4. Dielectric Strength

• The ideal dielectric is nonconducting but practically no dielectric can be ideal. As the electric field applied to dielectric increases sufficiently, due to the force exerted on the molecules, the electrons in the dielectric become free. Under such large electric field, the dielectric becomes conducting due to presence of large number of free electrons. This condition of dielectric is called dielectric breakdown. All kinds of dielectrics such as solids, liquids and gases show the tendency of breakdown under large electric field. The breakdown depends on the nature of material, the time and magnitude of applied electric field and atmospheric conditions such as temperature, moisture, humidity etc.

Key Point : The minimum value of the applied electric field at which the dielectric breaks down is called dielectric strength of that dielectric.

• The dielectric strength is measured in V/m or kV/cm. It also can be stated as the maximum value of electric field under which a dielectric can sustain without breakdown. Once breakdown occurs, dielectric starts conducting and no longer behaves as dielectric. Hence all the dielectrics are assumed to be either ideal or are not in a breakdown condition.

 

5.  Utilization Factor

• The utilization factor of an electric field is defined as the ratio of the average electric field to the maximum value of an electric field. It is denoted by 'η'.

η = Utilization factor = E_avg / E_max

• The reciprocal of utilization factor is called inhomogenity of an electric field.

 

Ex. 5.6.1 Find the magnitude of  for a dielectric material in which |  | =0.15 mV/m and xe = 4.25.

Sol. : For a dielectric medium,

 

Ex. 5.6.2 A certain homogeneous slab of loss-less dielectric material is characterized by electric susceptibility of 0.12 and carries a uniform electric flux density inside of 1.6 nG/m². Determine the value of polarisation and electric field intensity.

AU : May-04, Marks 6

Sol. :

 

Ex. 5.6.3 A linear, homogeneous, isotropic dielectric material has Ɛr = 3.6 and is covering the space between z = 0 and z = 1. If V = - 6000 z volts in the material, find

 

Ex. 5.6.4 A dielectric slab of flat surface with the relative permittivity 4 is disposed with its surface normal to a uniform field with the flux density 1.5 C/m² . The slab occupies a volume of 0.08 m and is uniformly polarised. Determine,

a) The polarisation in the slab and b) The total dipole moment of slab.

AU : Dec-14, Marks 6

Sol. :

 

Examples for Practice

Ex. 5.6.5 Find the polarization in dielectric material with

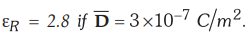
[Ans. : 1.9285 × 10^-7 C/m²]

Ex. 5.6.6 The polarization within a region having ƐR = 2.7 has the uniform value of

Review Questions

1. Explain the polarization in dielectric materials.

AU : Dec-17, May-18, Marks 6

2. Explain the properties of dielectric materials.

3. Explain in detail the behaviour of a dielectric medium in electric field.

4. Define dielectric polarization and dielectric constant.