Displacement Current Density and Displacement Current

Displacement Current Density and Displacement Current

AU Dec.-09, 14, 16, 18, May-06, 08, 09, 19

• For static electromagnetic fields, according to Ampere's circuital law, we can write,

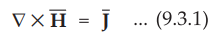
• Taking divergence on both the sides,

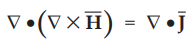
• But according to vector identity, 'divergence of the curl of any vector field is zero'. Hence we can write,

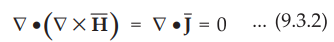
• But the equation of continuity is given by,

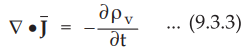
• From equation (9.3.3) it is clear that when ∂ρv / ∂t = 0,

• From equation (9.3.3) it is clear that when ∂ρv / ∂t = 0, then only equation (9.3.2) becomes true. Thus equations (9.3.2) and (9.3.3) are not compatible for time varying fields. We must modify equation (9.3.1) by adding one unknown term say 

• Then equation (9.3.1) becomes,

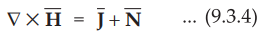
• Again taking divergence on both the sides

• Now we can write Ampere's circuital law in point form as,

• The first term in equation (9.3.6) is conduction current density denoted by  Here attaching subscript C indicates that the current is due to the moving charges.

• The second term in equation (9.3.6) represents current density expressed in ampere per square meter. As this quantity is obtained from time varying electric flux density. This is also called displacement density. Thus this is called displacement current density denoted by . With these definitions we can write equation (9.3.6) as,

 

1. Physical Significance of Displacement Current

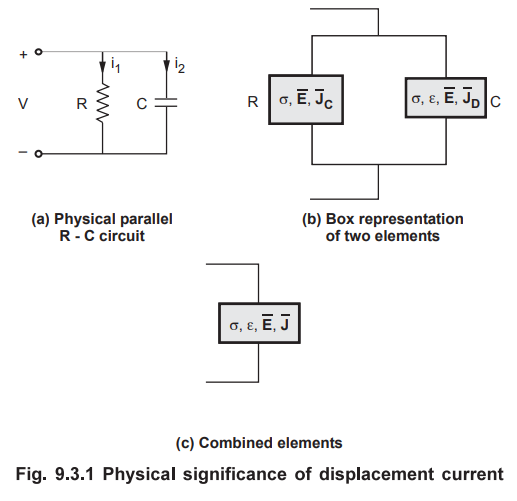
• Consider a parallel circuit a resistor R and a capacitor C as shown in the Fig. 9.3.1 (b). Consider that the parallel combination is driven by the time varying i.e. sinusoidal voltage V. It is obvious that the nature of current through the resistor R i.e. i₁ is different than that flowing through capacitor C i.e. i₂.

• Let the current flowing through resistor R be i₁ and the current flowing through capacitor C be i₂. The nature of the current flowing through the resistor R is different than that flowing through V the capacitor. The current through resistor is due _ Q to the actual motion of charges. Thus the current through resistor can be written as,

i₁  = V / R ..... (9.3.8)

• This current is called conduction current as the current is flowing because of actual motion of charges. Let it be denoted by i_C.

• Let A be the cross-sectional area of resistor, then the conduction current density is given by,

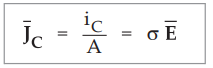
• Now assume that the initial charge on a capacitor is zero. Then for time varying voltage applied across parallel plate capacitor, the current through the capacitor is given by,

i₂ = C (dv/dt) ..... (9.3.10)

• Let the two plates of area A are separated by distance d' with dielectric having permittivity Ɛ in between the plates. Then we can write

i₂ = (ƐA / d') (dv / dt) ... (9.3.11)

• Now this current is called displacement current denoted by i_D. The electric field produced by the voltage applied between the two plates is given by,

E = V / 'd , dv / dt  ... (9.3.12)

or      V = (d') (E)

• Substituting value of V in equation (9.3.11), we get,

• Now the ratio of current to the area of plate is the current density. In this case it is displacement current density denoted by J_D.

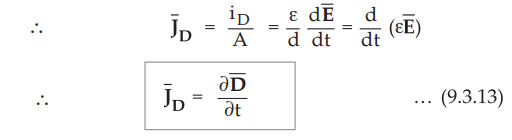
• Thus in a given medium, both the types of the currents, namely the conduction current current and the displacement current may flow. Hence the two current densities can be written as,

• The total current density is given by,

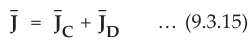
• Above equation (9.3.15) represents that instead of two separate elements in parallel, there is only one element which combines both R and C as shown in the Fig. 9.3.1 (c) where there is a capacitor filled with conducting dielectric as if such that both currents (conduction as well as displacement) are present.

Important Conclusions

• Some materials are good conductors while some are perfect dielectrics. But in some materials which are neither good conductor nor perfect dielectrics, both the current namely conduction current and displacement current may exist.

• For the electric field intensity  , let the time dependence be given by e^jωt, the total current density is given by,

 

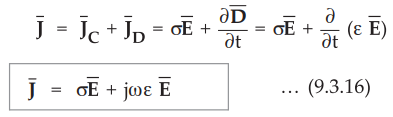
• Then the ratio of the magnitudes of the conduction current density to the displacement current density is given by,

 

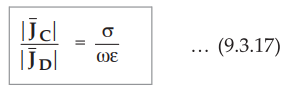
• Thus the ratio of the magnitudes of the conduction current density to the displacement current density depends on the properties of the medium (i.e. σ and p) and the frequency (i.e. ω). For a conductor, the value of conductivity σ is very large.

Key Point : So in conductor, the conduction current is very large as compared to the displacement current.

• While for a dielectric, the value of conductivity σ is very small.

Key Point : So in dielectric medium, the displacement current is greater as compared to the conduction current.

• In other words, if the ratio of the magnitudes of the current densities is greater than 1, the medium is conductor and if the ratio of the magnitudes is less than 1 then the medium is dielectric.

• Also the ratio represented above depends on frequency, a medium which is conductor at low frequency may become insulator at very high frequency.

Ex. 9.3.1 Show that the displacement current in dielectric of parallel plate capacitor is equal to the conduction current in the leads.

Sol. : Consider a parallel plate capacitor is connected to time varying voltage v as shown in the Fig. 9.3.3.

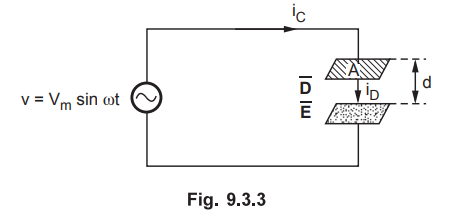
Let distance of separation between parallel plates be d. Let the area of plates in parallel be A. Let the applied voltage be v = V_m sin ωt.

The current flowing through the leads of the capacitor is conduction current and it flows when voltage is applied.

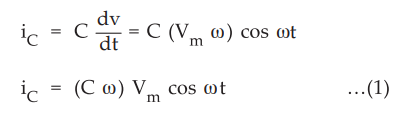
The displacement current is the current flowing through the dielectric between parallel plates. By definition it is given by,

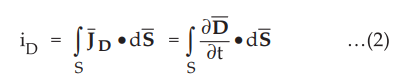
The flux density  between plates is normal to the plates. In other words,  and  are in same direction. Hence the dot product changes to simple multiplication. So we can write,

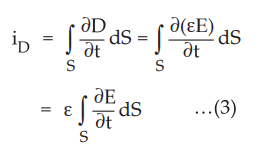
The electric field is related to potential through relation

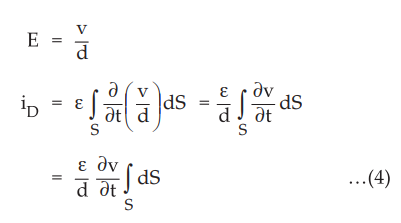
Now the integral term represents area of the plates i.e. A, hence we get,

i_D = Ɛ / d (d/dt) A ….. (5)

Now v is changing with respect to time we can change partial derivative to direct derivative and can modify equations as,

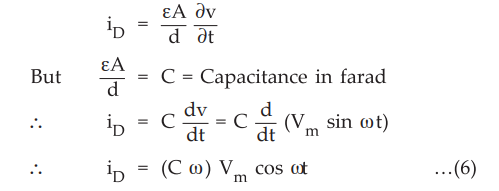
Thus from equations (1) and (6) we can prove that the displacement current in the dielectric of parallel plate capacitor is equal to the conduction current in the leads.

 

Ex. 9.3.2 a) Show that the ratio of the amplitudes of the conduction current density and displacement current density is o/roe for the applied field E = E_m cos ωt. Assume µ = µ₀.

b) What is this amplitude ratio if the applied field is E = E_m e^{-t/ τ} where τ is real ?

Sol. : a) The conduction current density is given by

J_C = σE = σEm cos  ωt

The displacement current density is given by

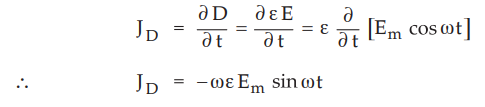
• The ratio of the amplitudes of the two densities is given by

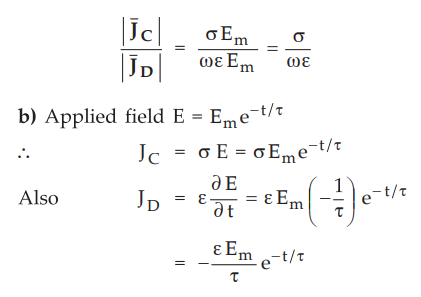
Now the ratio of the amplitudes of the two densities is given by

 

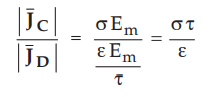
Ex. 9.3.3 Find the frequency at which conduction current density and displacement current density are equal in a medium with σ = 2 × 10^-4 Ʊ/m and Ɛ_r = 81.

Sol. : The ratio of amplitudes of the two current densities is given as 1, so we can write,

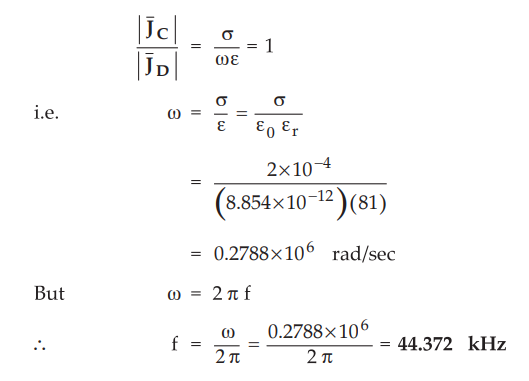
Hence, the frequency at which the ratio of amplitudes of conduction and displacement current density is unity, is 44.372 kHz.

 

Ex. 9.3.4 In a material for which σ = 5.0 Sim and Ɛ_r = 1, the electric field intensity is E = 250 sin 10¹⁰ t V/m. Find the conduction and displacement current densities, and the frequency at which both have equal magnitudes.

AU : Dec.-16, Marks 5

Sol. : The conduction current density is given by

JC = σ E = 5(250sin 10¹⁰ t)

= 1250 sin 10¹⁰ t A/m²

The displacement current density is given by

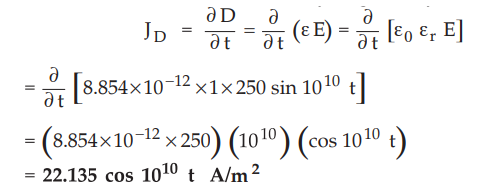
For the two densities, the condition for magnitudes to be equal is,

 

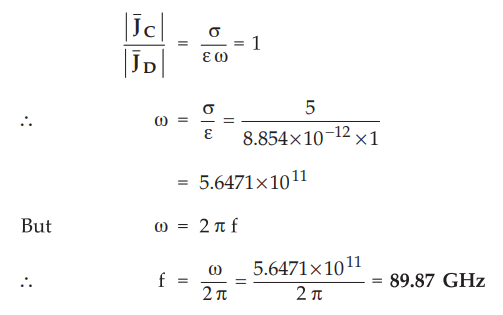
Ex. 9.3.5 Find amplitude of displacement current density in air near a car antenna where field strength of F.M. signal is

Sol. : The displacement current density is given by,

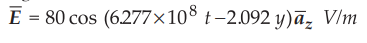
Sol. : The displacement current density is given by,

Ex. 9.3.6 Find amplitude of displacement current density in the free space within a large power distribution transformer where,

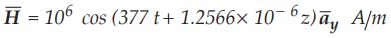
Sol. : According to ampere circuital law for free space,

 

Ex. 9.3.7 The conduction current flowing through a wire with conductivity σ = 3 × 10⁷ S/m and relative permeability Ɛ_r = 1 is given by I_c = 3 sin mt mA. If 10⁸ rad/sec,find the displacement current.

Sol. : The magnitude of conduction current density is given by,

Similarly the magnitude of displacement current density is given by,

As conduction and displacement currents are in quadrature, the displacement current is given by,

I_D = 88.542 cos 10⁸ t µA

 

Ex. 9.3.8 A circular cross-section conductor of radius 2 mm carries a current ie = 2.5 sin (5xl08f)pA What is the amplitude of the displacement current density if σ = 35 MS/m and Ɛ_r = l

AU : May-09, Marks 8

Sol. : The magnitude of conduction current density is given by,

Thus the magnitude of displacement current density is given by,

 

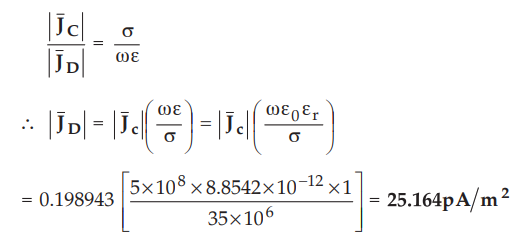
Ex. 9.3.9 A parallel plate capacitor with plate area of 5 cm2 and plate separation of 3 mm has a voltage of 50 sin 10³ t V applied to its plates. Calculate the displacement current assuming Ɛ = 2 Ɛ₀.

Sol . :

The displacement current density is given by

 

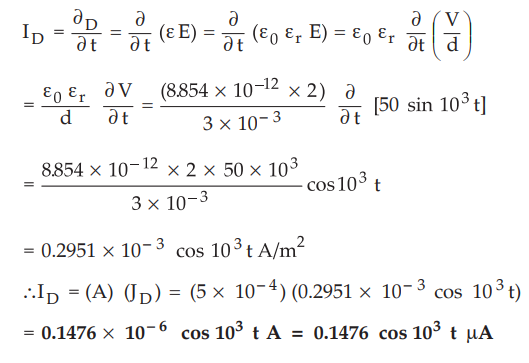
Examples for Practice

Ex. 9.3.10 A No 10 copper wire carries a conduction current of 1 amp at 60 Hz. Calculate the displacement current in the wire. For copper assume,

Ɛ = Ɛ₀, µ = µ₀  σ = 5.8 × 10⁷ Ʊ/m.

[Ans.: 0.05755 × 10^-15 A]

Ex. 9.3.11 A parallel plate capacitor with a plate area of 5 cm² and plate separation of 3 mm has a voltage 50 sin 10³t V applied to its plates. Calculate the displacement current assuming Ɛ = 4_Ɛ0.

[Ans.: 0.2951 cos 10³t µA]

Ex. 9.3.12 Find the amplitude of the displacement current density,

a) In the air near car antenna where the field strength of FM signal is,

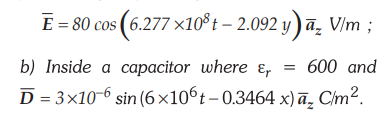
[Ans.: 0.4446 A/m²,18 A/m²]

Review Questions

1. What is displacement current ? Show that the displacement current in the dielectric of a parallel plate capacitor is equal to the conduction current in the leads.

AU : May-09, Marks 16

2. Differentiate conduction and displacement current and derive the same. Explain the need of displacement current in Maxwell's equations.

AU : May-08, Marks 16

3. What do you mean by displacement current ? Write down the expression for the total current density.

AU : May-06, Marks 8