Efficiency of a Transformer

Efficiency of a Transformer

AU:Oct.-02,April-98,99,03,04,Dec.-97,03,07,08,13,15,19,May-05,07,08,12,15,19, Nov.-04

• Due to the losses in a transformer, the output power of a transformer is less than the input power supplied.

Power output = Power input - Total losses

Power input = Power output + Total losses = Power output +P_i + P_Cu

The efficiency of any device is defined as the ratio of the power output to power input. So for a transformer the efficiency can be expressed as,

η = Power output / Power input = Power output / Power output + P_i + P_Cu

• Now power output = V₂ I₂ cos ϕ where cos ϕ = Load power factor. The transformer supplies full load of current I₂ and with terminal voltage V₂.

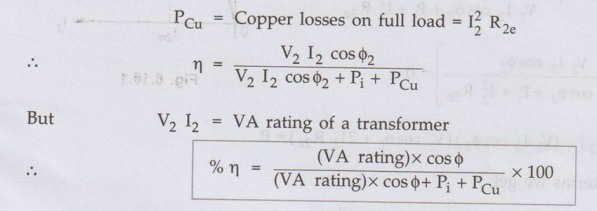
• This is full load percentage efficiency with I₂ = Full load secondary current.

• But if the transformer is subjected to fractional load then using the appropriate values of various quantities, the efficiency can be obtained.

Let n = Fraction by which load is less than full load = Actual load Full load / Full load

• For example, if transformer is subjected to half load then, n = Half load / Full load = (1/2)/1 = 0.5

• When load changes, the load current changes by same proportion.

New 1₂ = n (I₂) F.L.

•Similarly the output V₂I₂cos ϕ₂ also reduces by the same fraction. Thus fraction of VA rating is available at the output.

• Similarly as copper losses are proportional to square of current then,

New P_Cu = n² (P_Cu )F.L.

The copper losses get reduced by n² while iron losses remain same.

• In general for fractional load the efficiency is given by,

where n = Fraction by which load is less than full load.

For all types of load power factors lagging, leading and unity the efficiency expression does not change and remains same.

1. Condition for Maximum Efficiency

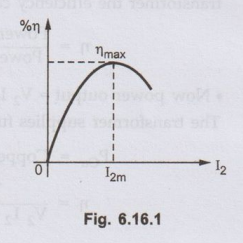
• The load current at which the efficiency attains maximum value is denoted as I2m and maximum efficiency is denoted as η_max.

• The efficiency is a function of load i.e. load current I₂ assuming cos ϕ₂ constant. The secondary terminal voltage V₂ is also assumed constant.

• The graph of efficiency against load current is shown in the Fig. 6.16.1.

So for maximum efficiency

So condition to achieve maximum efficiency is that,

Copper losses = Iron losses i.e. P_i = P_Cu

2. Load Current I_2m at Maximum Efficiency

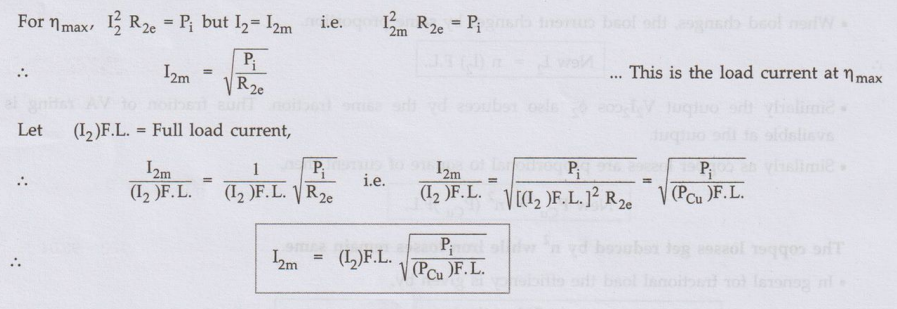
This is the load current at η_max interms of full load current.

3. kVA Supplied at Maximum Efficiency

• For constant V2 the KVA supplied is function of load current.

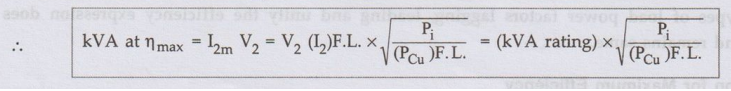
• Substituting condition for η_max in the expression of efficiency, we can write expression for η_max as,

Ex. 6.16.1 The primary and secondary windings of a 500 kVA transformer have resistance of 0.4 Ω and 0.001 Ω respectively. The primary and secondary voltages are 6600 V and 400 V respectively. The iron loss is 3 kW. Calculate the efficiency on full load, the load power factor being 0.8 lagging. AU: Oct.-02, Marks 8

Sol.:

Ex. 6.16.2 A 600 kVA, single phase transformer when working at u.p.f. has an efficiency of 92 % at full load and also at half load. Determine its efficiency when it operates at unity p.f. and 60 % of full load. AU: April-03, Marks 10

Sol. :

Ex. 6.16.3 Calculate the efficiency at half, full load of a 100 kVA transformer for power factor of unity and 0.8. The copper loss is 1000 W at full load and iron loss is 1000 W. AU: Dec.-03,08,15, May-12, Marks 10

Sol. :

Ex. 6.16.4 A 200 kVA, single phase transformer has an efficiency of 98 % at full load 0.8 p.f. lag. If the maximum efficiency occurs at three quarters full load, calculate the iron loss and full load copper loss. AU May-05, Dec.-07, Marks 8 Sol. :

Ex. 6.16.5 A 50 kVA, 11 kV/400 V transformer has a core loss of 500 W and a full load copper loss of 600 W. Calculate the efficiency on unity power factor at full load. Find the load for maximum efficiency and the iron and copper losses corresponding to this load. AU : May-15, Dec. -19,Marks 8

Sol. :

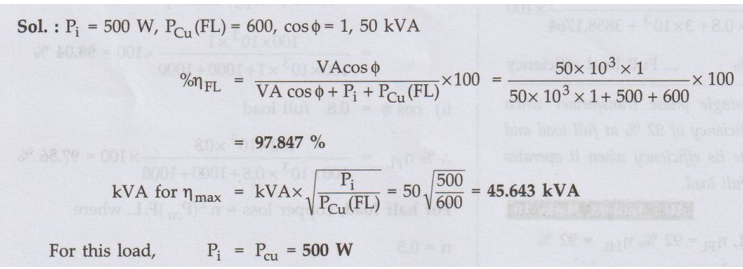
Ex. 6.16.6 The maximum efficiency of a single phase 250 kVA, 2000/250 V transformer occurs at 80 % of full load and is equal to 97.5 % at 0.8 p.f. Determine the efficiency and regulation on full load at 0.8 p.f. lagging if the impedance of the transformer is 9 percent. AU: Nov.-04, Marks 10

Sol. :250 KVA, 2000 / 250 V

Ex. 6.16.7 For the transformer of single phase, 5 kVA, 200V/400V, 50 Hz, the equivalent circuit is shown in Fig. 6.16.2. Calculate the following:

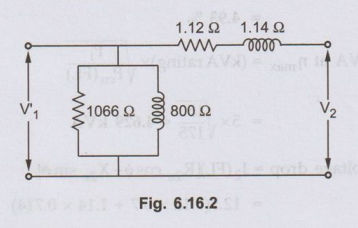
i) the efficiency of the transformer at 75% loading with load power factor = 0.7.

ii) At what load or KVA the transformer will be operated at maximum efficiency? Also calculate the value of maximum efficiency.

iii) The regulation of the transformer at full load 0.8 power factor lag.

iv) What should be the applied voltage to the LV side when the transformer delivers rated current of 0.7 power factor lagging at a terminal voltage of 400 V?

Sol. :

Review Questions

1. What do you understand by efficiency of a transformer?I

2. A 100 kVA transformer has iron loss of 2 kW and full load copper loss 1 kW.

Calculate the efficiency of the transformer at

i) Full load unity p.f. ii) Half load unity p.f. 

[Ans.: 97.087 %, 95.6937 %]

3. The efficiency of a 200 kVA, single phase transformer is 98 % when operating at full load 0.8 lagging p.f. the iron loss in the transformer is 2000 watt. Calculate the

i) Full load copper loss

ii) Half load copper loss and efficiency at half load. 

(Ans. 1265.306 W, 316.326 W, 97.186 %)

4. A 500 kVA transformer has an iron loss of 500 W and full load copper loss 700 W. Calculate the efficiency at 3/4 th full load and 0.8 power factor. AU: April-04 

[Ans. % η= 99.7029%]

5. A 100 kVA, 2.2 kV/220 V, 50 Hz transformer has an iron loss of 900 W and full load copper loss of 1000 W. Determine the efficiency at full load 0.8 pf. AU Nov.-04 

[Ans. : η = 97.68%]

6. A 250 kVA, single phase transformer has 98.135 % efficiency at full load and 0.8 lagging p.f. The efficiency at half load and 0.8 lagging p.f. is 97.751 %. Calculate the iron loss and full load copper loss. 

[Ans.: P_i = 2000.18 watt, P_C = 1800.69 watt ]

7. The efficiency of a 200 kVA, single phase transformer is 98 % when operating at full load 0.8 lagging p.f. the iron loss in the transformer is 2000 watt. Calculate the: i) Full load copper loss ii) Half load copper loss and efficiency at half load 

(Ans. η% = 97.186 %)

8. A single phase transformer working at unity p.f. has an efficiency of 90 % at half of full load and full load of 500 kW. Determine its iron and full load copper loss. AU: April-99 

[Ans.: P_cu (F. L.) = 37037.037 W, P_i = 18518.517 W]

9. Show that the maximum efficiency in transformer occurs when its variable loss is equal 100 to constant loss. AU: Dec.-13, May-07, 08, Dec.-09, Marks 6

10.A 5 kVA, 220/110 volts, 1 phase transformer has a maximum efficiency of 96.97 % at 0.8 p.f. lagging. It has a core loss of 50 watts and the full load regulation at 0.8 p.f. lagging is 5 %. Find the efficiency and regulation at full load 0.9 p.f. lagging. 

[Ans.: % η=93.231 %, % R = 3.968 %]

11.A 250 kVA single phase transformer has iron loss of 1.8 kW. The full load copper loss is 2000 watts. Calculate i) Efficiency at full load, 0.8 lagging p.f. ii) kVA supplied at maximum efficiency. iii) Maximum efficiency at 0.8 lagging p.f. AU: April-98, Dec.-97 

[Ans.: 98.135 %, 237.1708 kVA, 98.137 %]

12. A 11000/230 V, 150 kVA, 1-phase, 50 Hz transformer has core loss of 1.4 kW and F.L. Cu loss of 1.6 kW. Determine i) The kVA load for maximum efficiency and the value of maximum efficiency at unity p.f. ii) The efficiency at half F.L. 0.8 p.f. leading. AU May-08, Marks 8 

[Ans. : i) 140.3121 kVA, 98.043% ii) 97.087%]