Statistics and Numerical Methods: Unit III: Solution of Equations and Eigenvalue Problems
Eigen values of a Matrix by Power Method
Solved Example Problems | Solution of Equations and Eigenvalue Problems
The power method is an iterative technique. The method may not converge very fast. We can accelerate the convergence as well as get Eigenvalues of magnitude intermediate between the largest and smallest by shifting.
FIGENVALUES OF A MATRIX BY POWER METHOD
The
power method
The
power method is an iterative technique. The method may not converge very fast.
We can accelerate the convergence as well as get Eigenvalues of magnitude
intermediate between the largest and smallest by shifting. The power method
with its variations is fine for small matrices. However, if a matrix has two
Eigenvalues of equal magnitude, the method fails in the successive
normalization factors alternate between two numbers. The duplicated Eigenvalue
in this case is the square root of the product of the alternating normalisation
factors. If we want all the Eigenvalues for a larger matrix, there is a better way.
1.
Find the numerically largest Eigenvalue of
2. Using power method, find all the Eigenvalues of
3.
Find the dominant Eigenvalue and the corresponding Eigenvector of
4.
Find the numerically largest Eigenvalue of
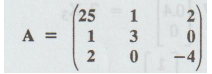
5.
Obtain by the power method, the dominant Eigenvalue and the corresponding
Eigenvector, correct to two decimal places, for the matrix
6.
Find the numerically largest Eigenvalue of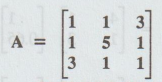 
by power method
Solution :
Statistics and Numerical Methods: Unit III: Solution of Equations and Eigenvalue Problems : Tag: : Solved Example Problems | Solution of Equations and Eigenvalue Problems - Eigen values of a Matrix by Power Method
Related Topics
Related Subjects
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation