Eigenvalue of a matrix by jacobi method for symmetric matrix

EIGENVALUE OF A MATRIX BY JACOBI METHOD FOR SYMMETRIC MATRIX

Let A be a given real symmetric matrix. Its eigenvalues are real and there exists a real orthogonal matrix B such that B^-1AB is a diagonal matrix D.

Jacobi's method consists of diagonalising A by applying a series of orthogonal transformations B₁, B₂, …, B_r such that their product B satisfies the equation D = B^-1AB

Rotation matrix

If P(x, y) is any point in the xy plane nie ( P(x,y) and if OP is rotated (O is the origin) in the clockwise direction through an angle θ, then the new position of P (x', y') is given by

x' = x cos θ - y sin θ;

y' = x sin θ + y cos θ

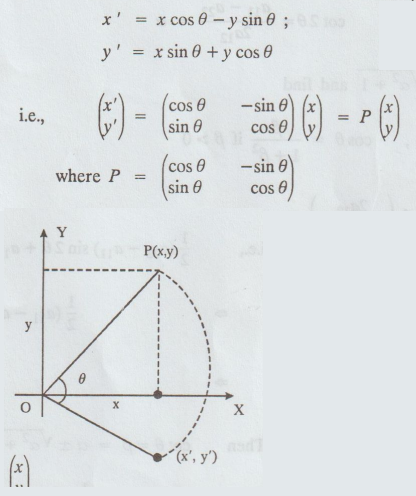
Hence P is called a Rotation matrix in the xy plane.

Here P is also an orthogonal matrix, since PP^T = I.

Eigenvalues of 2 × 2 matrix by Jacobi method

Step 1. Assume the most general orthogonal Rotation matrix of order 2 is

Step 2. To make B as a diagonal matrix.

Therefore, select so that b₁₂ = b₂₁ = 0

Step 4. Get D = P^TAP

The diagonal elements of D are the eigenvalues. The columns of P are the corresponding Eigenvectors.

Extension to Higher order Symmetric Matrices

Suppose we want to reduce the off-diagonal numerically largest element a_ij in (a_ij) _{n × n} matrix into zero.

First we select the Rotation matrix S₁ where

D₁ is a n × n matrix whose diagonal elements are 1 and all off-diagonal elements are zero except a_ii = cos θ, a_ij = cos θ, a_ij = - sin θ, a_ji = sin θ,

Now D₁ is orthogonal.

Find out B₁ = D^T₁AD₁ reducing b_ij (a_ij) into zero in B₁.

In the next step, take the largest off-diagonal element b_kt  in B^T₁ and reduce into zero to get

B₂ = D^T₂B₁D₂

Performing series of such rotation by D₁, D₂, D₃, , ... after k operations, we get

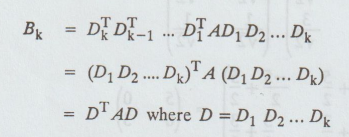
If B_k is diagonal matrix, we get immediately Eigenvalues of B_k and hence

of A. The Eigenvectors of A are the columns of the matrix D = D₁ D₂ ..D_k

1. Using Jacobi method, find the Eigenvalues and Eigenvectors of

2. Using Jacobi method, find the Eigenvalues and Eigenvectors of

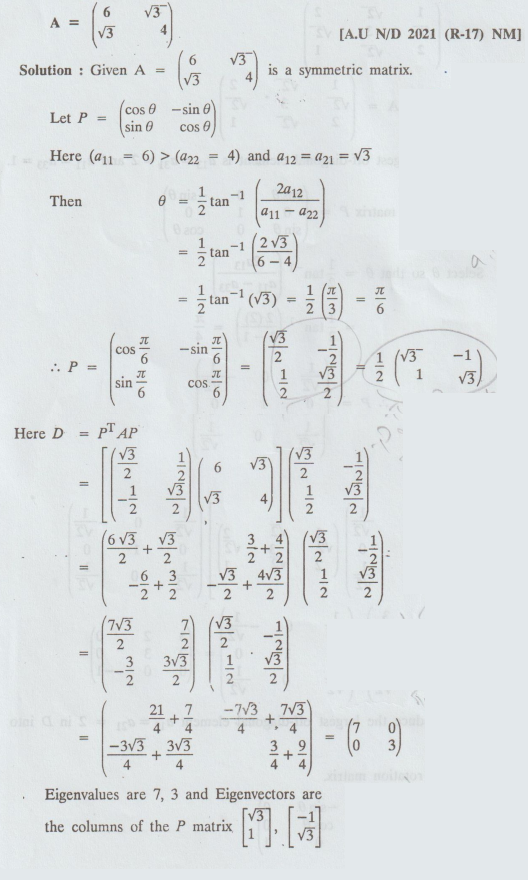
3. Find the Eigenvalues and Eigenvectors of the matrix

4. Find the Eigenvalues and Eigenvectors of the matrix

5. Apply Jacobi process to evaluate the Eigenvalues and Eigenvectors of the matrix

6. Apply Jacobi process to evaluate the Eigenvalues and Eigenvectors of the matrix

Solution :

7. Find the Eigenvalues and Eigenvectors of the matrix