Basic Civil & Mechanical Engineering: UNIT I: b. Structural engineering
Elastic constants of materials
Structural engineering
There are three Elastic Constants of materials, viz., Young's Modulus, Modulus of Rigidity and Bulk Modulus of Elasticity.
ELASTIC CONSTANTS OF MATERIALS
There
are three Elastic Constants of materials, viz., Young's Modulus, Modulus of
Rigidity and Bulk Modulus of Elasticity. These moduli describe the
relationships between stress and strain and are explained in the following
sections:
1. HOOKE'S LAW
Hooke's
Law was formulated by Robert Hooke in 1678. Hooke's Law states:
“When
an elastic material is stresses within elastic limit, the stress induced in the
material is proportional to the strain. In other words, the ratio of axial
stress to the corresponding axial strain is a constant within the limit of
proportionality.” That is, Stress oc Strain, i.e., foc e.
Therefore,
f = E e, where E is a constant. Hooke's Law is applicable to tension, compression
and shear. Hooke's Law forms the basis for evaluating the three elastic
constants.
2. YOUNG'S MODULUS or MODULUS OF ELASTICITY (E)
The
constant of proportionality concept was introduced by Thomas Young in 1807.
According
to Hooke's Law, stress f = Ee, where E is a proportionality constant. E is
known as Modulus of Elasticity or Young's Modulus.
Young's
Modulus of a material is defined as the ratio of the axial stress to the
corresponding axial or linear strain, within the elastic limit.
Young's
Modulus = E = Axial Stress / Axial Strain = f / e
Unit
for Young's Modulus is N/mm2 or Pa (Pascal). The above relation is
valid only for homogeneous materials of uniform cross-section, when loaded
axially within the limit of proportionality.
3. YOUNG'S MODULUS AND ELONGATION OF A BAR UNDER AXIAL LOAD
Let
a bar of uniform cross-section A and length 1 is subjected to an axial tensile
load P. Let dl be the elongation or deformation of the bar. E is
the Young's Modulus of the material of the bar.

4. MODULUS OF RIGIDITY or SHEAR MODULUS (G)
Hookes's
Law is assumed to apply to shear also. Modulus of Rigidity or Shear Modulus of
a material is the ratio of shear stress to the corresponding shear strain. This
ratio is a constant up to the elastic limit of the material. It is denoted by
G.

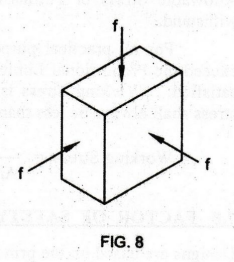
5. BULK MODULUS OF ELASTICITY (K)
See
Fig. 8. When a body is subjected to uniform direct stresses of equal intensity
(either tensile or compressive) in all the three mutually perpendicular
directions, then the ratio of the direct stress (f) to the corresponding
volumetric strain (ev) is constant up to the elastic limit. This elastic
constant is called Bulk Modulus of the material. It is denoted by K.
Bulk
Modulus = K = Direct Stress / Volumetric Strain
Volumetric
Strain (ev)
Due
to external loads, the longitudinal and lateral strains occur in an elastic
body. Therefore, the volume of the elastic body changes. The change in volume
dv (increase or decrease) of the elastic body on unit original volume V is
called the Volumetric Strain. It is denoted by ev.
Volumetric
Strain = ev = Change in Volume / Original Volume = dv / V
Therefore,
Bulk Modulus = K = Direct Stress / Volumetric Strain = f / ev
=
(P /A) / (dv/V) = PV/ A(dv).
6. POISSON'S RATIO (µ or 1/m )
When
a body is subjected to tensile load (axial load), it is subjected to axial
strain. There is elongation in the direction of the tensile load.
Simultaneously, there is a reduction in the transverse dimensions (lateral
dimensions). The ratio of the transverse strain (lateral strain) to the
corresponding axial strain (longitudinal strain) is constant within the
proportionality limit. This ratio is called Poisson's Ratio.
Poisson's
Ratio is named after Poisson, a French Mathematician. It is denoted by µ or
1/m.
Poisson's
Ratio = µ = 1/m = Lateral or Transverse Strain / Axial or Longitudinal Strain
7. WORKING STRESS or SAFE STRESS or PERMISSIBLE STRESS
While
designing the size of structural members, Working Stress much less than the
Proportional Limit is used. Working Stress is actually the stress developed in
the material when it is loaded. Allowable Stress or Permissible Stress is the
maximum stress which a material can safely withstand.
For
all practical purposes, working stress is equal to allowable stress. It should
not exceed the Proportional Limit. Only then, the stress-strain relationship of
Hooke's Law will be satisfied. Working Stress is also known as Safe Stress or
Permissible Stress. The working stress shall always be less than the Ultimate
Stress.
Working
Load = Working Stress / Area of Cross-section
8. FACTOR OF SAFETY
Designs
are based on the principle that the stresses to which structural members are
subjected are less than the proportional limit. On this basis, the Working
Stresses are prescribed. In structural steel, the working stress is kept much
below the yield strength to avoid excessive permanent deformations. The ratio
of yield strength to permissible working stress is called the Factor of Safety.
For
homogeneous and uniform materials like steel, aluminium, etc., a factor of
safety of 4 is used. For other materials like timber, which are highly
non-uniform due to the presence of knots, higher factor of safety is used.
In
concrete, there is no defined yield strength. But, the ultimate strength is
clear. Hence, for concrete, the factor of safety is fixed with reference to the
ultimate strength.
Factor
of Safety = Ultimate Stress / Working Stress
Factor
of safety is always greater than 1. Allowable Stresses are pre-determined for
different materials under different loading conditions. The determination of an
appropriate value for the factor of safety is a complex matter. It requires
considerable engineering judgment. Factor of safety depends on the following
considerations:
•
Quality of material and its degree of reliability
•
Type of loading whether static or dynamic, dead or live load, concentrated or
distributed load, etc., including nature and conditions of loading
•
Function of the member under design
•
Possible manufacturing or fabrication errors and workmanship
•
Possible type of maintenance
The
recommended factor of safety for different civil structures as per IS codes is
given in the following table:

For
steel structures, factor of safety is fixed with reference to the yield
strength and hence it is generally higher. Since the factor of safety is fixed
with reference to the ultimate strength for concrete structures, it is
generally lower.
9. RELATION BETWEEN ELASTIC CONSTANTS
Each
elastic material has four elastic constants. These constants are inter-related
with one another. If the values of any two constants are known for a material,
the other two constants may be easily determined using the following equations:
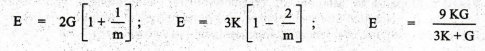
Basic Civil & Mechanical Engineering: UNIT I: b. Structural engineering : Tag: : Structural engineering - Elastic constants of materials
Related Topics
Related Subjects
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
