Electrical Properties of Materials

Unit - II

Electrical and Magnetic Properties of Materials

2(a) Electrical Properties of Materials

Classical free electron theory - Expression for electrical conductivity - Thermal conductivity expression - Quantum free electron theory :Tunneling - degenerate states Ferm i- Dirac statistics - Density of energy states Electron in periodic potential - Energy bands in solids - tight binding approximation - Electron effective mass concept of hole

 

Introduction

It is essential to study the various electrical properties of the solids for their specific applications.

In terms of electrical properties, all solid state materials are classified into three groups as conductors, semiconductors and dielectrics or insulators.

The selection of materials for different applications depends on their electrical properties as well as requirements of the job.

Electrical phenomena are caused by the motion of electrons in solids and find many applications in day-to-day activities.

Electrons in a metallic filament and the property of electrical resisivity of the material are used in incandescent lamps for heating and illumination in a variety of domestic and dustrial applications.

In recent times, the mobility of electrons is being exploited in solar cells, lasers, in the control of thermonuclear reactions and many other applications.

The chapter mainly deals with the electrical conduction, thermal conduction, density of states, number of electrons per unit volume in a metal etc.

Besides, it also deals with the classical, quantum free electron theories and band theory to explain the conductivity of the solid state materials.

Basic definition

It is necessary to know the basic relations in electrical conductivity to understand its derivation.

Ohm's Law

When an electrical current flows through a conductor, then the voltage drop across the conductor is given by the ohm's law

V=IR (or) I= V / R...(1)

where I - current in ampere,

R - resistance to the current flow in ohm

V - voltage drop across the conductor in volt.

Resistance (R)

The resistance R of a conductor is a geometry (length and area) and property dependent factor of the material used.

R ∝ l / A

R = ρ l / A = l / σ A ...(2)

Ρ - Proportionality constant known as resistivity (ohm m) ρ = 1/ σ

1- Length of the conductor (m)

A- Area of cross section (m²)

σ- Electrical conductivity (ohm^-1m^-1) (or) (mho m^-1) (or) siemens m^-1 (Sm^-1)

Current Density (J)

It is defined as the current per unit area of cross section of a current carrying conductor. If I is the current and A is the area of cross-section, then current density is given by

J = I / A ....(3)

Its unit is Am^-2

Electrical Field (E)

The electrical field E in a conductor of uniform cross section is defined as the potential drop (voltage) V per unit length.

E = V / l ...(4)

Its unit is Vm^-1

Electrical Conductivity (σ)

The amount of electrical charges (Q) conducted per unit time across unit area (A) of a conductor per unit applied electrical field (E) is defined as electrical conductivity.

It is denoted by o and it is given by

σ = Q / tAE

σ = Q / tAE = J / E

where J is the current density and it is given by ( Q / tA )

A second form of ohm's law is obtained by combining equations (1) and (2)

From eqn (1), V=IR

From eqn (2), R= l / σA 

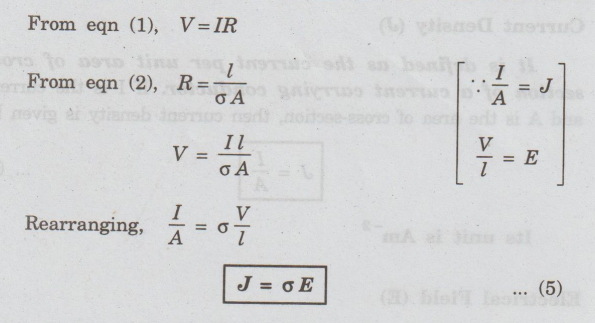
Rearranging, I / A = σ V / l

J = σ E ...(5)

Relation between Current Density J, Drift Velocity V_d and Mobility μ

 Let n be the number of charge carriers per unit volume (also called charge carrier density) in a conductor of length with uniform cross sectional area A. The current flow through the conductor is given by

I = Total charge / Time = Q/ t

= ne Al / t = ne Av_d ...(6)

where v_d = l / t is called the drift velocity. It is the average velocity gained by the charge carriers in the presence of an electrical field.

But, we know that J = I / A

Using the eqn (6), J is written as

J = ne Av_d / Avd =  ne v_d

J = nev_d ....(7)

But J=  σ E.

Therefore, the eqn (7) becomes

 σ E = nev_d

σ = ne v_d / E

Hence , σ = neμ ...(8)

 

gnibyo00A 8ser radi ni dold vd Benog

where μ = v_d / E  is called the mobility of the charge carrier. It is defined as the drift velocity per unit electric field. Its unit is m² V^-1 s^-1.

Free Electron theory of solids

It is well known that the electrons in the outermost orbit of the atom determine the electrical properties of a solid. The free electron theory of solids explains the structure and properties of solids through their electronic structures.

This theory is applicable to all solids, both metals and non-metals. It explains

• The behaviour of conductors, semiconductors and insulators.

• The electrical, thermal and magnetic properties of solids.

Main Stages of Free Electron theory of solids

(i) Classical free electron theory (Drude and Lorentz free electron theory)

This theory was proposed by Drude and Lorentz in the year 1900. According to this theory, the free electrons are mainly responsible for electrical conduction in a metal.

It obeys the laws of classical mechanics. Here, the free electrons are assumed to move in a constant potential.

(ii) Quantum free electron theory (Sommerfeld Quantum theory)

Quantum free electron theory was proposed by Sommerfeld in the year 1928. According to this theory, the electrons in a metal move in a constant potential.

It obeys the laws of quantum mechanics. The wave nature of electron is taken into account to describe the electron.

(iii) Zone theory or band theory of solids

This theory was proposed by Bloch in the year 1928. According to this theory, free electrons move in a periodic potential.

It explains electrical conductivity based on the energy bands.