Energy Stored in a Capacitor

Energy Stored in a Capacitor

AU : May-96, 04, 05, 06, 08,13, Dec.-03, 14, 17, 18

• It is seen that capacitor can store the energy. Let us fin d the expression for the energy stored in a capacitor.

• Consider a parallel plate capacitor as shown in the Fig. 5.17.1. It is supplied with the voltage V.

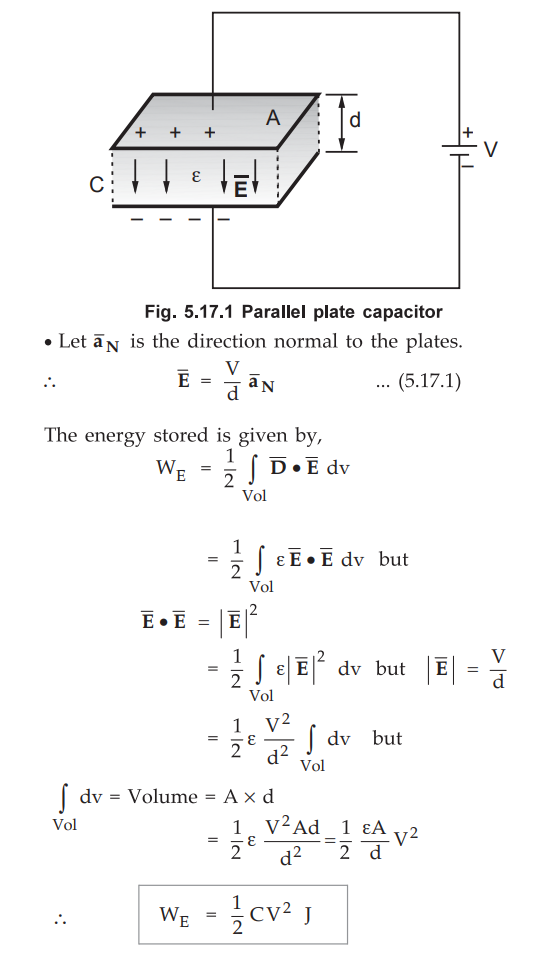
• If the dielectric is free space then there is increase in the stored energy if free space is replaced by other dielectric having Ɛ_r > 1 .

1. Energy Density

• As seen in earlier chapter, energy density is the energy stored per unit volume as volume tends to zero.

Ex. 5.17.1 Let A = 120 cm², d = 5 mm and Ɛ_R = 12 for a parallel plate capacitor -

a) Calculate the capacitance.

b) After connecting a 40 V battery across the capacitor, calculate E, D, Q and the total stored energy.

c) The source is now removed and the dielectric is carefully withdrawn from between the plates. Again calculate E, D, Q and the energy.

d) What is voltage between the plates ?

c) Though source and dielectric is removed, Q on the surface remains same.

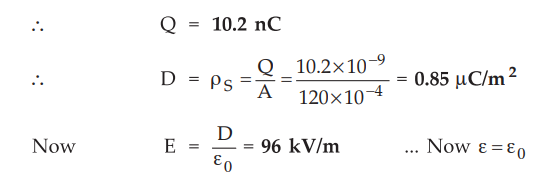
and as V is now not same across the plates, calculate W_E as,

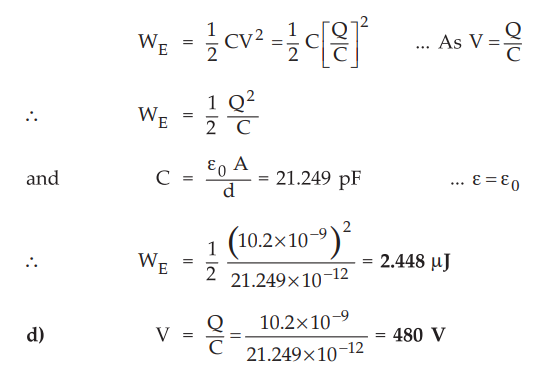
Ex. 5.17.2 A capacitor with two dielectrics is as follows : Plate area 100 cm , Dielectric 1 thickness = 3 mm, Ɛ_r1 = 3, Dielectric 2 thickness = 2 mm, Ɛ_r2 = 2. If a potential of 100 V is applied across the plates find the energy stored in each dielectric and potential gradient in each dielectric.

AU : May-96, 04, Marks 10

Sol. :

Ex. 5.17.3 A 4 mF capacitor is charged by connecting it across 100 V/d.c. The supply is disconnected and another uncharged 2 mF capacitor is connected across it. If leakage charge is negligible, determine the potential between the plates.

AU : May-05, Marks 6

Sol. : The arrangement is shown in the Fig. 5.17.3.

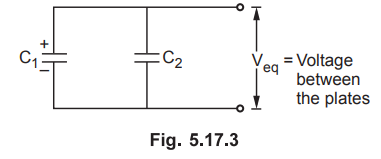
Initially when Ci is charged to 100 V d.c., the energy stored is,

This energy must remain same while voltage across the two must be same as V_eq. So total energy in the new arrangement is,

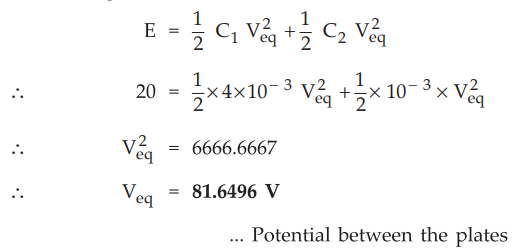
Ex. 5.17.4 Parallel plate capacitor is of area 1 m2 and has a separation of 1 mm. The space between the plates is filled with dielectric of Ɛr = 25. If 1000 V is applied, find the force squeezing the plates together.

AU : May-08, Marks 6

Sol. :

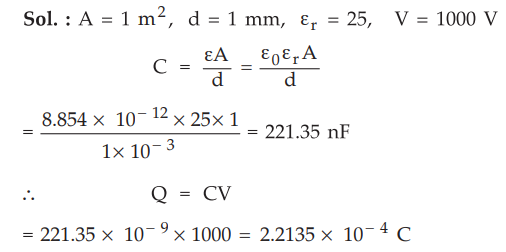
For the plate separation 'x', the capacitor is C = ƐA / x

 For the fixed voltage V across the plates,

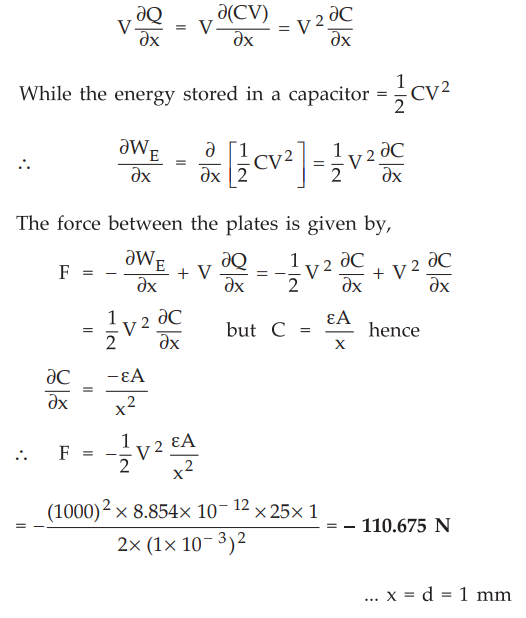
Ex. 5.17.5 Find the value of capacitance of a capacitor consisting of two parallel metal plates 30 cm × 30 cm surface area, separated by 5 mm in air. What is the total energy stored by the capacitor if the capacitor is charged to a potential differnece of 1000 V ? What is the energy density ?

AU : May-13, Marks 8

Sol. :

Ex. 5.17.6 A capacitor consists of two parallel metal plates 30 cm × 30 cm surface area, separated by 5 mm in air. Determine its capacitance. Find the total energy stored by the capacitor and the energy density if the capacitor is charged to a potential difference of 500 V ?

AU : Dec.-14, Marks 8

Sol. : Refer Example 5.17.5 for the procedure and verify the answer as :

C = 159.372 pF, W_E = 19.9215 µJ

Energy density = 0.04427 J/m³          

Examples for Practice

Ex. 5.17.7 A parallel plate capacitor of width 'W separation of plates 'd' and length 'L' is partially filled with a dielectric slab of permittivity Ɛr. Prove that the force acting on the dielectric is, 

Ex. 5.17.8 A 2 pF capacitor is charged by connecting it across a 100 V d.c. supply. It is now disconnected and then it is connected across another 2µF capacitor. Assuming no leakage, determine the p.d. between the plates of each capacitor and energy stored.

[Ans.: 70.7106 V]

Ex. 5.17.9 A pair of 200 mm long concentric cylindrical conductors of radii 50 mm and 100 mm, is filled with a dielectric with Ɛ = 10 Ɛ₀. A voltage is applied between the conductors  which establishes 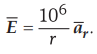 Calculate :

a) Capacitance b) Voltage applied c) Energy stored.

[Ans.: a) 160.518 pi, b) 693.1471 kV, c) 38.5606 J]

Ex. 5.17.10 An air capacitor consists of a parallel square plates of 50 cm side and is charged to a potential difference of 250 V, when plates are 1 mm apart. Find the work done in seperating the plates from 1 to 3 mm. Assume perfect insulation.

[Ans.: 138.34 µJ]

 Review Questions

1. Prove that the energy required to charge a capacitor C by a voltage V is W = 1/2 CV²

AU : Dec.-03,18, May-06, Marks 8

2. Derive the energy density of capacitance.

AU : Dec.-17, Marks 7