Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Equation of sinusoidally varying emf and current (sinusoidal functions)
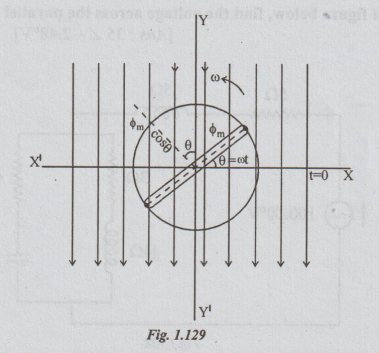
Consider a rectangular coil with N turns. It is rotated in an uniform magnetic field in anticlockwise direction.
EQUATION OF SINUSOIDALLY VARYING EMF AND CURRENT (SINUSOIDAL
FUNCTIONS)
Consider
a rectangular coil with N turns. It is rotated in an uniform magnetic field in
anticlockwise direction.
Let
B = flux density of the field in weber/m2 (or) tesla
ω = angular velocity of the coil in radians/sec.
The
time is measured from the positive x-axis. After 't' seconds of rotation, the
coil is rotated through an angle θ = ωt.
In
this position, resolve the flux into two components. One component is
perpendicular to the plane of the coil. The other one is parallel to the plane
of the coil. The component of flux at right angles to the plane of the coil is
ϕ
= ϕm cos θ
=
ϕm cos ωt
Only
this flux links with the coil. The instantaneous emf induced
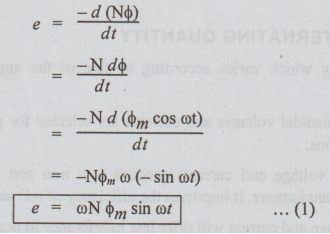
When
sin ot is maximum (=1), then e is maximum and is denoted by Em
i.e.,
Em = ω Nϕm … (2)
Therefore,
the above equation for e becomes
e
= Em sin ωt = Em sin θ ... (3)
The
above equation is called the standard sinusoidal equation of the voltage. The
value of e depends upon sin θ.
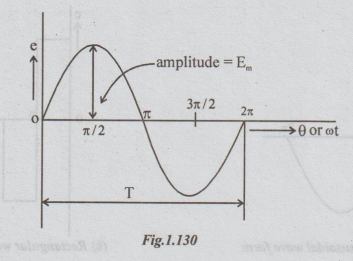
The
above equation can be graphically represented as below. It is called voltage
wave form.
Note:
1.
The magnitude of maximum emf depends upon (a) angular velocity (b) number of turns
and (c) maximum flux. It does not depend upon the angle.
2.
The value of instantaneous emf e depends upon 0. In other words it depends upon
the time for a given speed (since θ = wt).
3.
The standard equation of sinusoidally varying voltage is, instantaneous voltage
= maximum voltage x sin θ.
4.
The standard form for a sinusoidally varying current is
i
= Im × sin θ
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : - Equation of sinusoidally varying emf and current (sinusoidal functions)
Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation