Exchange Interaction and Ferromagnetism

EXCHANGE INTERACTION AND FERROMAGNETISM

The ferromagnetic property is exhibited by transition elements such as iron, cobalt, and nickel at room temperature and rare earth elements like gadolinium and dysprosium.

The ferromagnetic materials possess parallel alignment of dipoles. This parallel alignment of dipoles is not due to the magnetic force existing between any two dipoles. The reason is that the magnetic potential energy is very small and it is smaller than thermal energy.

The electronic configuration of iron is 1s², 2s², 2p⁶, 3s²,3p⁶,3d⁶, 4s². For iron, the 3d subshell is an unfilled one. This 3d subshell have five orbitals.

For iron, the six electrons present in the 3d subshell occupy the orbitals such that there are four unpaired electrons and two paired electrons as shown in figure 2.28.

These four unpaired electrons contribute a magnetic moment of 4ẞ. This arrangement shows the parallel alignment of four unpaired electrons.

The parallel alignment of dipoles in iron is not due to the magnetic interaction. It is due to the Pauli's exclusion principle and electrostatic interaction energy.

The Pauli's exclusion principle and electrostatic interaction energy are combined together and constitute a new kind of interaction known as exchange interaction. The exchange interaction is a quantum mechanical concept.

The exchange interaction between any two atoms depends upon the interatomic separation between the two interacting atoms and the relative spins of the two outer electrons. The exchange interaction between any two atoms is given by

E_ex= - J_e S₁ S₂

where J_e is the numerical value of the exchange integral,S₁ and S₂ are the spin angular momenta of the first and second electrons.

The exchage integral value is negative for a number of elements. Therefore, the exchange energy value is negative (minimum energy configuration) when the spin angular momentum S₁ and S₂ are opposite direction.

Hence, antiparallel alignment of dipole is favoured. This explains the antiparallel alignment of dipoles in antiferromagnetic materials.

In some materials like iron, cobalt and nickel the exchange integral value is positive. The exchange energy is negative when the spin angular momentum is in the same direction. This will produce a parallel alignment of dipoles.

 A plot between the exchange integral and the ratio of the interatomic separation to the radius of 3d orbital (r/r_d) is shown in figure 2.29.

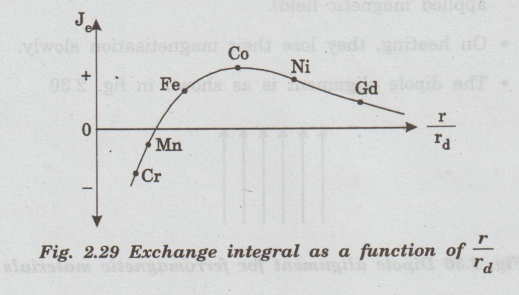
For the transition metals like iron, cobalt, nickel and gadolinium the exchange integral is positive, whereas for manganese and chromium the exchange integral is negative.

The positive value of the exchange integral represents the material as ferromagnetic and the negative exchange integral value represents the material as antiferromagnetic.

In general, if the ratio, r/r_d >3, the material is ferromagnetic, otherwise the material is antiferromagnetic. It should be noted that manganese is suitably alloyed so that r/r_d> 3, and it will become ferromagnetic.

Ferromagnetic materials

The materials which exhibit the ferromagnetism are called ferromagnetic materials.

Properties

• All the dipoles are aligned parallel to each other due to the magnetic interaction between the dipoles.

•They have permanent dipole moment. They are strongly attracted by the magnetic field.

• They exhibit magnetisation even in the absence of magnetic field. This property of ferromagnetic materials is called as spontaneous magnetisation.

• They exhibit hysteresis (lagging of magnetisation with applied magnetic field).

• On heating, they lose their magnetisation slowly.

• The dipole alignment is as shown in fig. 2.30

• The magnetic susceptibility is very high and it depends iston temperature.

It is given by

Χ = C / T-θ (for T > θ, paramagnetic behaviour T < θ, ferromagnetic behaviour)

where C is Curie constant and θ ferromagnetic Curie temperature.

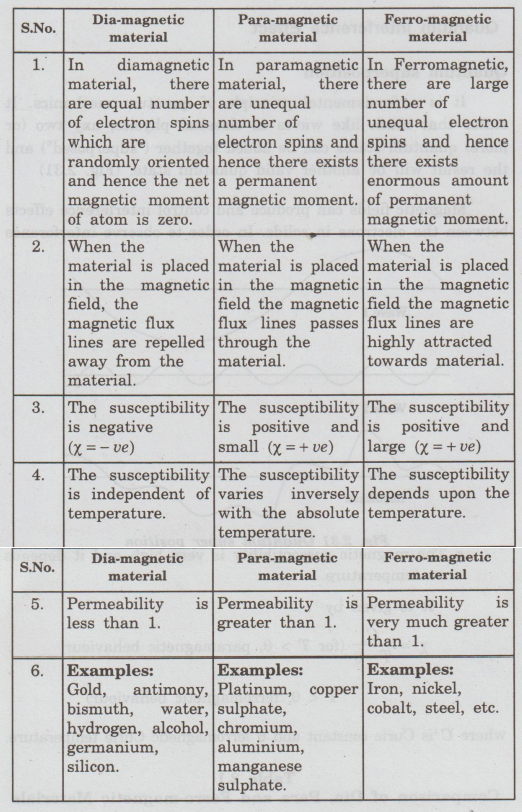
Table 2.1

Comparison of Dia, Para and Ferro-magnetic Materials

Quantum Interference Effect

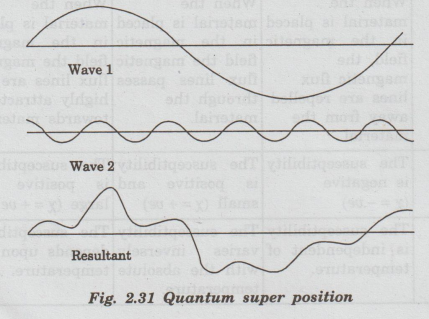
Quantum superposition

It is a fundamental principle of quantum mechanics. It states that much like waves in classical physics, any two (or more) quantum states can be added together ("superposed") and the result will be another valid quantum state. (Fig. 2.31)

Magnetic fields can produce and control interference effects between the electrons in solids. In order to observe interference effects between different electron waves, their phase has to be maintained.

The phase coherence length L_ϕ is the distance travelled by an electron without changing its phase. The phase of an electron wave is generally destroyed when electrons interact inelastically with defects in the lattice.

In general, ballistic electrons with a mean free path l_e much larger than sample dimensions L, (i.e.l_e >> L,) travel through the lattice without scattering. Therefore they show interference effects.

Applications of Quantum Interference Effect

Quantum interference effect is being applied in a growing number of applications, such as the

• Superconducting Quantum Interference Device (SQUID).

• quantum cryptography

• quantum computing and quantum interference transistor.