Probability and complex function: Unit V: Ordinary Differential Equations
Exercise 5.2 (method of variation of parameters)
Problems with Answer | Ordinary Differential Equations
Probability and complex function: Unit V: Differential equations : Exercise 5.2
EXERCISE
5.2
Solve
the following by using method of variation of parameters :
1. (D2+1) y = x.
[Ans. y = x + C1
cos x + C2 sinx.]
2. y'' + 3y' + 2y = x2.
[Ans.
y = (1/2 x2 – 3/2 x+ 7/4) + C1e-2x+
C2e-x]
3.
x2y'' + 4xy' + 2y = ex.
[Ans. y = C1x-2 +
C2x-1 + x-2 ex]
4. (D2 + 1) y = sinx + cos x
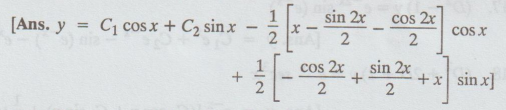
5.
(D2 + 4) y = tan 2x [AU, Nov.
2001]
6.
y'' + 4y = 4 sec2 2x [A.U A/M
2017 R-13]
[Ans. y = C1 cos 2x + C2
sin 2x - 1 + (sin 2x) log (sec 2x + tan 2x)]
7.
y' + y =1 / 1 + sin x
[Ans. y = C1 cos x + C2
sin x − (x cos x – sin x + 1) + sin x log (1 + sin x)]
8.
d2y/dx2 + y = sec
x tan x
[Ans. y = C1 cos x + C2
sin x + x cos x - sin x + (sin x) log sec x]
9.
y"- 2y' + 2y = ex tan x
[Ans. y = ex [C1
cosx + C2 sin x – cos x log (sec x + tanx)]]
10. y" - 2y' = ex. sin x
[ Ans. y = C1 + C2 e2x – ½ ex
. sinx ]
11. y'' - 2y' + y = ex/x
[ Ans. y = ( C1 + C2x) ex
– xex + ( x log x) ex]
12. y"+2y' + y = logx
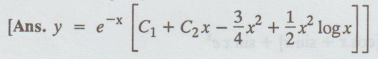
13. d2y/dx2
– y = 2/1 + ex
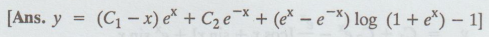
14.
y'' + y' – 2y = 1/1 - ex
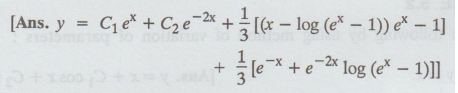
15. d2y/dx2
+ 3 dy/dx + 2y = 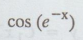
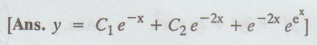
16. y'- 3y' + 2y = cos (e-x)
[ Ans.
y = C1ex + C2e2x – e2x –
e2x cos (e-x)]
17. (D2 - 1) y = e ̄-2x sin (e- ̄x)
[Ans. C1ex + C2e2x
–sin( e-x )– ex cos (e-x)]
18. (D2 + 2D + 2) y = e-x sec3 x
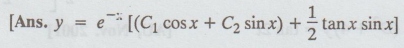
19. x2d2y/dx2 + x dy/dx – y = x2 log x
[ Ans. y = C1x + C2/x
+ x2/9 (3 log x – 4) ]
20. x2d2y/dx2 - 4x dy/dx + 6y = sin (log x)
[ Ans. y = C1x2 + C2x3
+ 1/10 [sin( log x) + cos (log x)]
21. x2d2y/dx2 + 2 dy/dx + y = e-x /x2 [A.U M/J 2013]
[ Ans.
C1e-x + C2e-x – e-x log
x ]
22. x2d2y/dx2 + x dy/dx – y = x2 log x
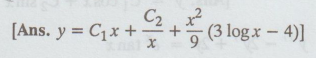
23.
y'' + 7y' - 8y = e2x [ Ans. y
= Aex + Be-8x + 1/10 e2x ]
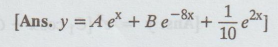
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Problems with Answer | Ordinary Differential Equations - Exercise 5.2 (method of variation of parameters)
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
