Exercise 5.3. (a) cauchy-euler

EXERCISE 5.3. (a)

Solve the following differential equations :

1. (x²D²+xD-1) y = 0 where D = d/dx  [A.U. May, 2001]

2. (x² D² - 3xD + 4) y = x² cos (log x) [A.U N/D 2010]

[Ans. y = x² + (A + B log x) – x² cos (log x ))

3. (x³ D³ + 2x² D2 - xD + 1)y = log x

[ Ans. y = x² (A + B log x) - x² cos (log x)]

4. (x² D² + xD -9) y = 5/x²  

[Ans. y = Ax³ + B/x³ – 1/x² ]

5. (x²D² + 4xD +2) y = x² + 1 / x²

[Ans. y = A / x + B/x² + x² /12 – 1/x² log]

 [A.U A/M 2008] [A.U. M/J 2013]

6. (x² D² + xD + 1) y = sin (2 logx) sin (logx)

[A.U A/M 2005, A.U Tvli N/D 2009]

 [Ans. y = A cos (log x) +B sin(log x) – 1/16 sin (3log x) – 1/4 logx cos (logx)]

7. (x² D² - 2xD - 4) y = 32 (log x².

 [Ans. y = Ax⁴ + B/x – [8 (log x)² – 12(log x) + 13]]

8. (x² D² - xD + 4) y = x² sin (logx)

[Ans. y = x[Acos(√3 logx) + Bsin(√3 log x)] – 1/13 x²[2 cos (logx) - 3 sin (log. x)]

9. (x2 D2 + 4xD + 2) y = sinx

[Ans . y = A/x + B/x² – 1/x² sin x]

10. (x2 D2 + 2xD - 20) y = (x + 1)2.

11. (x² D² - 4x D + 6) y = 42 / x

[Ans. y = C₁x² + C₂x³ + 1/x⁴ ]

12. (x² D² + 1) y = 3x²

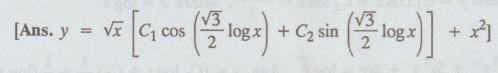
13. x²y" - xy' + y = x

Ans. y = (C₁ + C₂ logx) x + x / 2 (logx) ²

14. x²y" - 3xy' + 4y = x², y (1) = 1, y ' (1) = 0

Ans. y = x² [1 - 2 logx + 1/2 (logx) ²]

15. x²y'' - xy' - 3y = x² logx

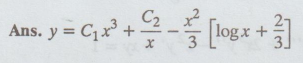
16. x²y" + xy' + y = 4 sin (log x)

Ans. y = C₁ cos (log x) + C₂ sin (logx) - 2 log x cos (log x)

17. x²y'' + 3xy' + 5y = x cos (logx) + 3

Ans. y = 1/x [C₁ cos (2 logx) + C₂ sin (2 log x)]

+ x/65 [4 sin (logx) + 7 cos (logx)] + 3/5

18. x²y" - 3xy' - 5y = cos (logx) UA]

Ans. y = Ax ̄1 + B-112 sin (logx) + 3 cos (log x)]

19. x²y" + 3y' + y = sin (log x) / x²

Ans. y = 1/x (A log x + B) + 1/2x² cos (log x)

20. x²y'' + xy' - 9y = x² log x

Ans. y = Ax³ + B / x³ -  x² / 25 [5 logx +4]

21. x³y'" + 3x²y" + xy' + y = x + log x

[A.U A/M 2015 R8]

22. x²y'' - 3xy' + 5y = x² sin (log x)

 [A.U A/M 2017 R8]

23. x²y" + xy' + y = sin (log x²)

Ans. y = e^2z C₁ cos z + C₂ sin z - sin 2z/3, where z = logx

24. x³y'' + 5x²y' + 4xy = logx

Ans. y = (C₁ logx + C₂)1/x² + (logx - 2)

25. (x² D² + xD + 4) y = cos (logx) +x sin (log x)

Ans. y = (C₁ cos 2z + C₂ sin 22) + 1/3 cos z – e^z / 10  (cos z - 2 sin z), where z = log x

26. x⁴y'"' + 2x³ y" - x²y' + xy=1

Ans. y = (C₁z + C₂) e^z + C3e^-z + e^-z / 4, where z = logx