Faraday’s Law and Lenz’s Law

Faraday’s Law and Lenz’s Law

AU : May-95, 04, 06, 07, 09, 14, 17, 18, 19, H Dec.-97, 03, 04, 06, 08, 14, 15, 16, 19

• In year 1820, Prof. Hans Christian Oersted demonstrated that a compass needle deflected due to an electric current. After ten years, Michael Faraday, a British Scientist, proved that a magnetic field could produce a current.

• According to Faraday's experiment, a static magnetic field can not produce any current flow. But with a time varying field, an electromotive force (e.m.f.) induces which may drive a current in a closed path or circuit. This e.m.f. is nothing but a voltage that induces from changing magnetic fields or motion of the conductors in a magnetic field. Faraday discovered that the induced e.m.f. is equal to the time rate of change of magnetic flux linking with the closed circuit.

Statement of Faraday's Law : "The electromotive force (e.m.f.) induced in a closed path (or circuit) is proportional to rate of change of magnetic flux enclosed by the closed path (or linked with the circuit)." The statement of Faraday's law was based on the experiments performed by Faraday and the experiments are commonly known as Faraday's experiment. He observed that when a closed path moves in a magnetic field, current is generated and hence e.m.f. The same observations he made with closed path kept fixed and the magnetic field was varied. The effect is commonly called electromagnetic induction.

Faraday's law can be stated as,

e = -N d ϕ / dt volts

where          N = Number of turns in the circuit,

e = Induced e.m.f.

Let us assume single turn circuit i.e. N = 1, then Faraday's law can be stated as,

e = - d ϕ / dt volts ... (9.2.2)

• The minus sign in equations (9.2.1) and (9.2.2) indicates that the direction of the induced e.m.f. is such that to produce a current which will produce a magnetic field which will oppose the original field.

• In 1834, Henri Frederic Emile Lenz postulated the law. Thus according to Lenz's law, the induced e.m.f. acts to produce an opposing flux.

 Statement of Lenz's Law : " The direction of induced e.m.f. is such that it opposes the cause producing it. i.e. changes in the magnetic flux." Consider a closed path with N turns then by Faraday's law, the induced e.m.f is given by,

e =-N d ϕ / dt Volts

• where negative sign indicates that the e.m.f is induced is such that to produce current which will oppose the cause producing it by producing a magnetic field which opposes the original field.

• Let us consider Faraday's law. The induced e.m.f. is a scalar quantity measured in volts. Thus the induced e.m.f. is given by,

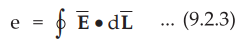
• The induced e.m.f. in equation (9.2.3) indicates a voltage about a closed path such that if any part of the path is changed, the e.m.f. will also change.

• The magnetic flux ϕ passing through a specified area is given by

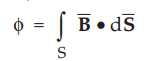
where          B = Magnetic flux density

• Using above result, equation (9.2.2) can be rewritten as

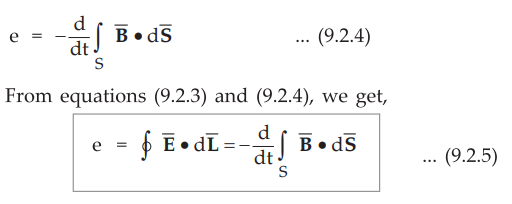
• The variation of flux ϕ with respect to time t can be caused due to any one of the following conditions.

a) By having a stationary closed path in a time varying  field.

b) By having a time varying closed path in a static 

c) By having a time varying closed path in a time varying  field.

• When an e.m.f. is induced in a stationary closed path due to time varying B field, the e.m.f. is called statically induced e.m.f. or transformer e.m.f. When the e.m.f. is induced in a time varying closed path due to a static  field, the e.m.f. is called dynamically induced e.m.f. or motional e.m.f.

 

1. A Stationary Closed Path in a Time Varying Field - Statically Induced E.M.F. or Transformer E.M.F.

• The condition in which a closed path is stationary and the magnetic field  is varying with time is as shown in the Fig. 9.2.1.

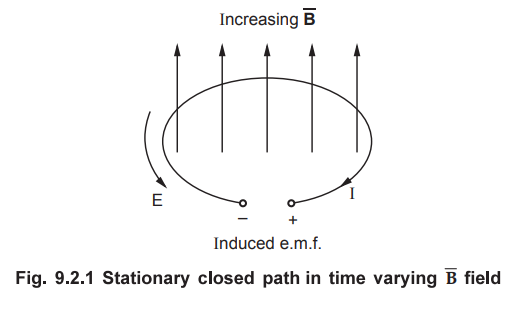
• A closed circuit stationary, while a magnetic flux density varying with time.

• The closed circuit in which e.m.f. is induced is stationary and the magnetic flux is sinusoidally varying with time. From equation (9.2.5) it is clear that the magnetic flux density is the only quantity varying with time. We can use partial derivative to define relationship as  may be changing with the co-ordinates as well as time. Hence we can write,

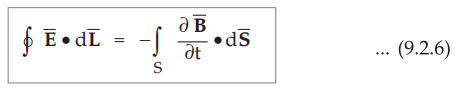
• This is similar to transformer action and e.m.f. is called transformer e.m.f.. Using Stake's theorem, a line integral can be converted to the surface integral as

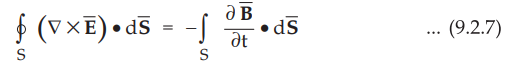
Assuming that both the surface integrals taken over identical surfaces.

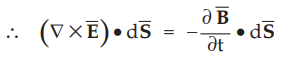
Hence Finally

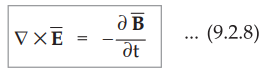
• Equation (9.2.8) represents one of the Maxwell's equations. If  is not varying with time, then equations (9.2.6) and (9.2.8) give the results obtained previously in the electrostatics.

 

2. A Moving Closed Path in Static  Field - Dynamically Induced E.M.F. or Motional E.M.F.

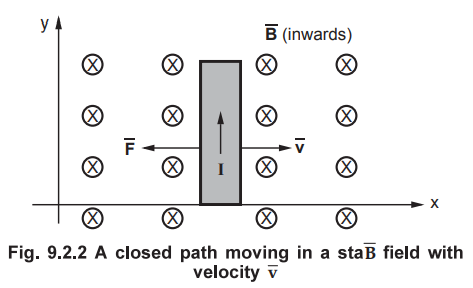
The condition in which magnetic field  is stationary while a closed path is moving or revolving is as shown in the Fig. 9.2.2.

• Secondly magnetic field is stationary, constant not varying with time while the closed circuit is revolved to get the relative motion between them. This action is similar to generator action, hence the induced e.m.f. is called motional or generator e.m.f.

• Consider that a charge Q is moved in a magnetic field  at a velocity . Then the force on a charge is given by,

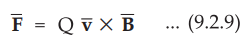
• But the motional electric field intensity is defined as the force per unit charge. It is given by,

• Thus the induced e.m.f. is given by

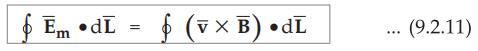
• Equation (9.2.11) represents total e.m.f. induced when a conductor is moved in a uniform constant magnetic field.

• If the directions of velocity  with which conductor is moving and the magnetic field  are mutually perpendicular to each other, then the induced e.m.f. is given by,

e = Blv sin90° = Blv ... (9.2.12)

where          l = Length of straight conductor.

 

3. Moving Closed Path in a Time Varying  Field

• A moving closed path in a time varying B field represents a general case in which both the e.m.f.s i.e. transformer e.m.f. and motional e.m.f. are present. Thus the induced e.m.f. is the combination of two e.m.f.s. Hence the induced e.m.f. for a moving closed path in a time varying field  can be expressed as,

 

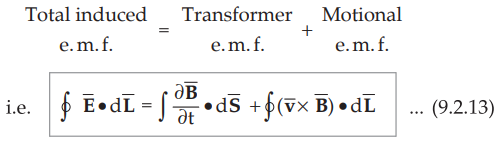
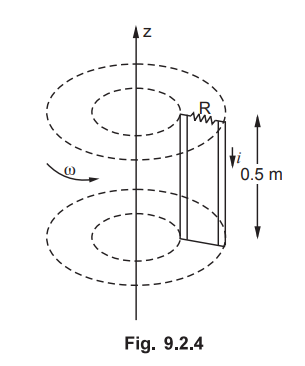
4. Faraday's Disc Generator

• A Faraday disc generator consists a rotating disc, with its axis located horizontally. This disc is placed in uniform magnetic field . To make the contact with the disc, two brushes are used. One of the brushes is located at the rim while the other brush is located at the axis as shown in the Fig. 9.2.5.

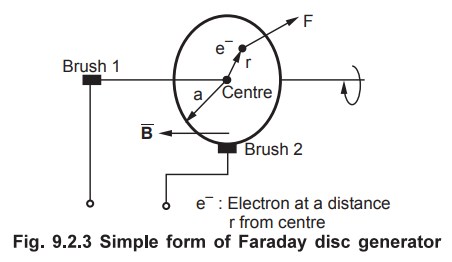
• Assume that the magnetic field  is along the axis of the disc. In other words, the magnetic field is perpendicular to the plane of the disc. Let a be the radius of the disc. Assume that the disc is rotated at constant angular velocity ro expressed in rad/sec. Consider that an electron is located at a distance r from the centre of the disc C.

• As the disc rotates at an angular velocity ro rad/sec, the electron moves at a velocity which is given by,

v = ωr m/s

• Thus the force exerted on electron is given by,

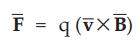
where q is charge on electron.

• But the electric field intensity can be written as,

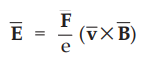
• Thus the magnitude of the electric field intensity is given by,

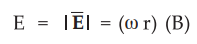
• The field acts radially inwards. Thus e.m.f. produced between centre of the disc and rim of the disc is given by,

 

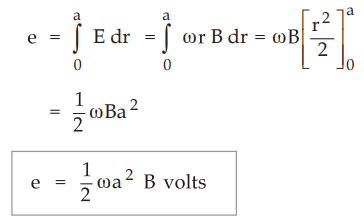
Ex. 9.2.1 A rectangular conducting loop with a resistance of 0.2 Ω rotates at 500 r.p.m. The vertical conductor at rr = 0.03 m is in the field 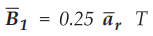  and other conductor is at r2 = 0.05 m and in the field  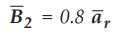T. Find current flowing in the loop.

Sol. :

The inner conductor which is at r₁ = 0.03 m rotates at 500 r.p.m. Thus inner conductor rotates with 500 / 60 revolutions per second. As in one second, the distance covered is (2 π r) meter, for the inner (500/60) (2 π r)  meters. Then the linear velocity for inner conductor is given by

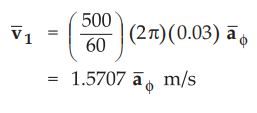
Similarly for outer conductor, linear velocity is given by

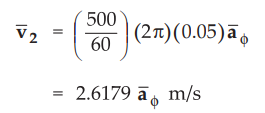
= 2.6179 a m/s

Here  is not varying with time, it is constant in  direction. Thus under such condition, the induced e.m.f. is given by,

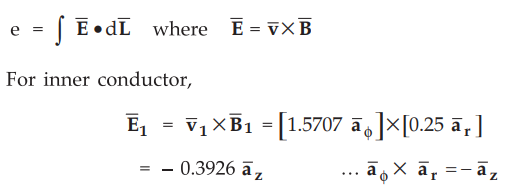
Both the conductors are vertical. Let us assume that length of each conductor be 0.5 m.

 

Ex. 9.2.2 A circular loop conductor lies in plane z = 0 and has a radius of 0.1 m and resistance of 5 Ω. Given 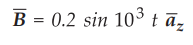T, determine the current in the loop.

AU : Dec.-14, Marks 8

Sol. :

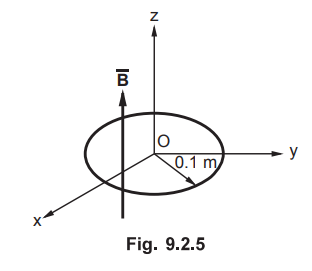
To find current in the loop, let us first calculate induced e.m.f.

A circular loop is in z = 0 plane.  is in z-direction which is perpendicular to the loop. So  is perpendicular to the circular loop.

Hence total flux is given by

With cylindrical co-ordinate system,

 

Ex. 9.2.3 The circular loop conductor having a radius of 0.15 m is placed in X-Y plane. This loop consists of a resistance of 20 Ω  as shown in the Fig. 9.2.6. If the magnetic flux density is 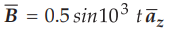T. Find current flowing through this loop.

AU : May-17, Marks 7

Sol. : The circular loop conductor is in X-Y plane.  is in direction which is perpendicular to X-Y plane.

Hence, we can write,

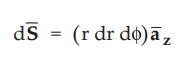
Total flux is given by

 

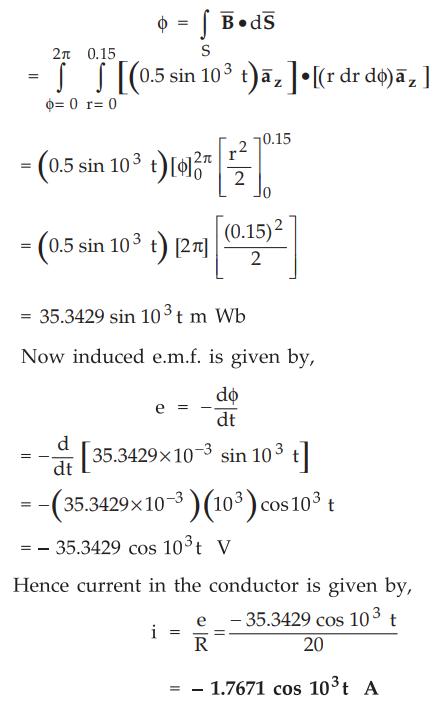
Ex. 9.2.4 A circular loop of wire is placed in a uniform magnetic field of flux density 0.5 wb/m . The wire has 200 turns and frequency of rotation of 1000 revolutions/minute. If the radius of the coil is 0.2 m, determine (1) the induced emf when the plane of the coil is 60° to the flux lines and (2) the induced emf, when the plane of the coil is perpendicular to the field.

AU : Dec.-15, Marks 8

Sol. : The velocity of circular loop is given by

V = (1000 / 60) (2 πr) m/s = (1000 / 60) (2 π × 0.2) = 20.944 m/s

1) Now the angle made by plane of coil to the flux lines is 60^Ω i.e. θ = 60 ^Ω . Hence induced emf is given by,

 e = Blv sin θ = B[(2πr)N] v sin θ

= 0.5[(2 π × 0.2)(200)](20.944)sin60° = 2.2793 kV

2) When plane of coil is perpendicular to flux lines,

θ = 90,

e = e = Blv sin 90° = e = Blv

= (0.5)(2 π ×  0.2 ×  200)(20.944) = 2.632 kV

 

Ex. 9.2.5 A conducting cylinder of radius 7 cm and height 50 cm rotates at 600 r.p.m. in a radial field 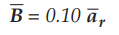T. Sliding contacts at the top and bottom are used to connect a voltmeter as shown in the Fig. 9.2.7. Calculate induced voltage.

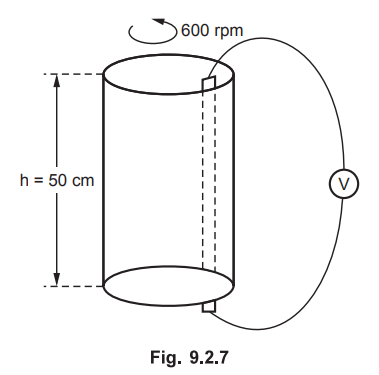
Sol. : A conducting cylinder rotates in the direction as shown in the Fig. 9.2.7. It rotates at 600 r.p.m. Means in 1 sec there are 10 revolutions. The radius of the cylinder is 0.07 m. In 1 revolution, the distance travelled by the cylinder is (2 πr) m i.e. (2 × π × 0.07) m. Hence in 10 revolutions, it travels (2 × π × 0.07 × 10) m distance. So the linear velocity is given by,

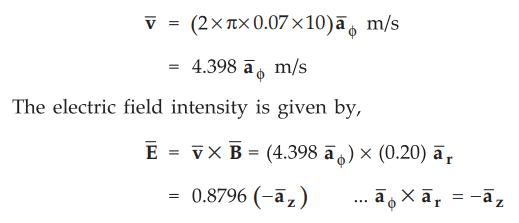
Here field is not varying with time. The cylindrical conductor is rotating. Each vertical element of it on the curved surface cuts same flux and thus the induced voltage is same. As these elements are as if in parallel, the e.m.f. induced in one element is same as that total e.m.f.

 

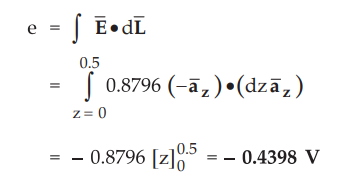
Ex. 9.2.6 A conductor of length 0.5 m moves in a uniform magnetic field of density 1.1 T at a velocity of 30 m/s. Calculate the induced voltage in the conductor when the direction of motion is perpendicular to the field.

AU : May-04, Marks 2

Sol. : The induced e.m.f. is given by,

e = Blv sin θ = (1.1) (0.5) (30) sin π / 2 = 16.5 V

As field and direction of motion are perpendicular to each other, θ = π / 2

 

Ex. 9.2.7 A conductor 1 m in length is parallel to the z-axis and rotates at 1500 rev/mm with radius of 25 cm. Find the induced voltage if the radial field is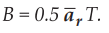 

AU : May-95, Dec.-19, Marks 6

Sol. : Here the magnetic flux is constant while the path is rotating with speed of 1500 r.p.m. The field intensity is given by,

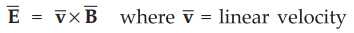
 In one minute there are 1200 revolutions which corresponds to 20 revolutions in one second. The distance covered in one second is (2 πr) meter. Hence  in 20 revolutions the distance travelled is (40 πr) meter. The conductor rotates in ϕ direction. Hence linear velocity is given by,

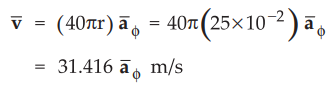
Hence the electric field intensity is given by,

 

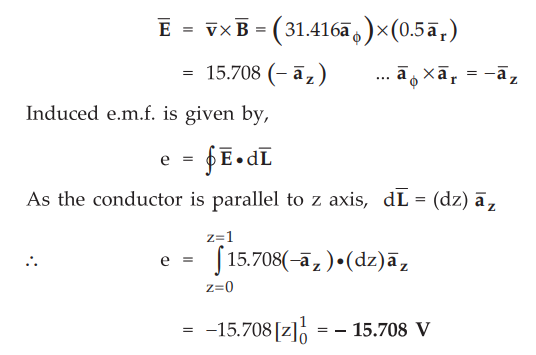
Ex. 9.2.8  The total flux at the end of a long bar magnet is 300µWb. The end of the bar magnet is drawn through a 1000 turn coil in 1/100 seconds. What is the e.m.f induced in the coil ?

AU : Dec.-97, Marks 4

Sol. : The induced e.m.f in the coil is given by,

e = N (d ϕ / dt) = N (change in flux/ change in time)

= (1000) 300 × 10^-6 / (1/1000) = 30 V

 

Ex. 9.2.9 Calculate the induced e.m.f. at t = 10 sec. when the flux through each turn of a 200 turn coil is t (t-1) mWb.

AU : May-07, Marks 4

Sol. :

 

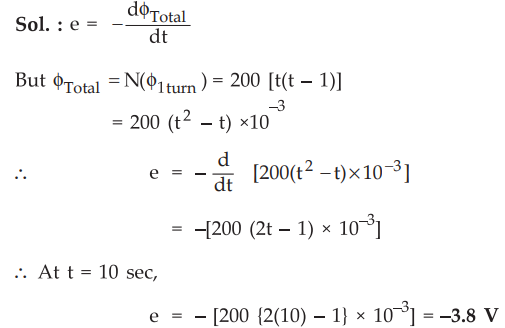
Ex. 9.2.10 A conducting loop of radius 10 cm lies in the z = 0 plane.

The associated 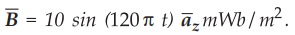. Calculate the voltage induced in the loop.

AU : May-14, Marks 5

Sol. : Given : r = 10 cm = 10 × 10^-2m,

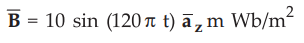
A conducting circular loop is in z = 0 plane and  is in z-direction which is perpendicular to loop. Hence  is perpendicular to the loop.

 

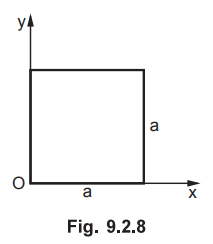
Ex. 9.2.11 A square loop of side a lies in the xy plane as shown. A magnetic field exists in the region directed along the z direction and varies with time and space as 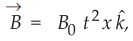 where B₀ is appropriately dimensioned.

Calculate the emf developed in the loop. If the x component of the induced electric field is zero, obtain an expression for the electric field induced and show that the line integral of the electric field correctly gives the emf calculated.

AU : Dec.19, Marks 15

Sol . :

Now x component is to be made zero and equating z component with equation (1)

The contribution by CO is also zero as x = 0 for this line and hence E = 0. The only contribution is from AB with x = a.

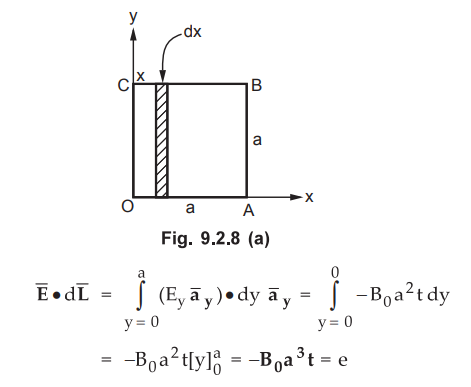
Thus the line integral of the electric field intensity correctly gives the e.m.f. calculated.

 

Examples for Practice

Ex. 9.2.12 Determine the e.m.f. induced about the path r = 0.5, z = 0, t = 0 .

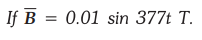
[Ans.: - 2.9609 V]

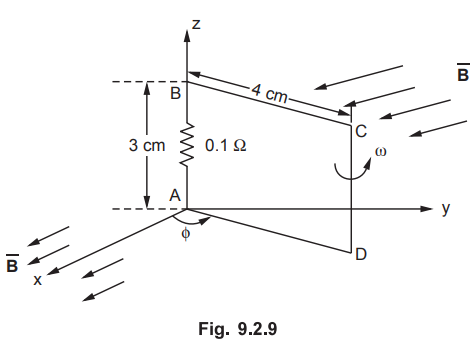
Ex. 9.2.13 A loop shown in the Fig. 9.2.9 is inside a uniform magnetic field

 If side d.c. of the loop cuts flux lines at frequency of 50 Hz and the loop lies in the y-z plane at t = 0, find

i) the induced e.m.f. At t = 1 ms.

ii) the induced current at t = 3 ms.

[Ans.: 5.8248 mV, 0.15249 A]

Ex. 9.2.14 An area oj 0.65 m² in the plane z = 0 encloses a filamentary conductor. Find the induced voltage if

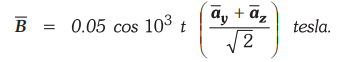
[Ans.: 22.98 sin 10³t V]

Review Questions

1. State and explain Faraday's law of electromagnetic induction.

2. Explain following

i) Motional e.m.f. ii) Transformer e.m.f.

3. Define the Faraday's laws. What are the different ways of e.m.f. generation? Explain with the governing equations and suitable example for each.

AU : Dec.-08, 03, Marks 16

4. What are the different ways of e.m.f. generation? Explain with the governing equations and suitable practical examples.

5. Write short note on Faraday’s law of electromagnetic induction.

6. Explain the concept of emf induction in static and time varying magnetic field.